Федеральное агентство по образованию российской федерации

БИЙСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (филиал)

Государственного образовательного учреждения высшего профессионального образования

«Алтайский государственный технический университет им. И. И. Ползунова»

(БТИ АлтТГУ)

Кафедра экономики и предпринимательства

Расчетное задание по статистике

Вариант 5

Выполнил:

студент группы ПИЭ-41 Фролов А. С.

Проверилa: Кабакова В. Н.

Бийск 2006

Задание 5.1

Имеются данные за 2002г. о работе предприятий отрасли:

Таблица 1. – Исходные данные задания 5.1

№ п/п	Готовый выпуск, тыс. т	Прибыль, тыс. руб.
1	1,4	43,1
2	1,7	52,5
3	1,8	55,6
4	1,9	58,8
5	2	61,9
6	1,9	58,8
7	1,8	55,6
8	1,7	52,5
9	1,4	43,1
10	1	30,6
11	1,5	44,2
12	1,7	52,5
13	1,8	54,8
14	1,9	58,6
15	2	61,9
16	1,9	54,5
17	1,8	51,5
18	1,7	48,6
19	1,2	35
20	1,4	38,4
Итого:	33,5	1012,5

Для изучения зависимости между прибылью и годовым выпуском продукции произведите группировку предприятий по количеству продукции, образовав пять групп с равными интервалами. По каждой группе отдельно и в совокупности предприятий в целом определите:

• число предприятий;

• количество выпущенной продукции - всего и в среднем на одно предприятие;

• сумму прибыли - всего и в среднем на одно предприятие.

Для измерения тесноты связи между количеством годового выпуска и суммой прибыли вычислите коэффициент корреляции, составьте линейное уравнение регрессии, постройте график корреляционной зависимости.

Решение:

Произведем группировку предприятий по количеству продукции, образовав 5 групп предприятий с равными интервалами. Интервал группировки определим по формуле:

x_max=2;x_min=1;n=5.

Составим группировочную таблицу:

Определим:

1.число предприятий по каждой группе.

2. количество выпущенной продукции - всего и в среднем на одно предприятие;

3. сумму прибыли - всего и в среднем на одно предприятие.

Среднее количество продукции и прибыли находим по формуле:

Таблица 2 – Группировка предприятий.

Группировка предприятий по кол-ву продукции		Число предприятий	Количество выпущенной продукции		Сумма прибыли
Xiнач.	Xiкон		Всего по группе	в среднем на предприятие	Всего по группе	в среднем на предприятие
1	1,2	2	2,2	1,1	65,6	32,8
1,2	1,4	3	4,2	1,4	124,6	41,533
1,4	1,6	1	1,5	1,5	44,2	44,2
1,6	1,8	8	14	1,75	423,6	52,95
1,8	2	6	11,6	1,933	354,5	59,083
Итого:		20	33,5	1,675	1012,5	50,625

Для определения тесноты связи между количеством годового выпуска и суммой прибыли вычислим коэффициент корреляции, составим линейное уравнение корреляции, построим график корреляционной зависимости.

Уравнение тренда имеет вид:

Найдем a₀иa₁ по формулам

.

Составим таблицу промежуточных расчетов:

Таблица 3 - Промежуточные расчеты.

№ п/п	Готовый выпуск, тыс. т	Прибыль, тыс. руб.	Готовый выпуск в квадрате	Прибыльв квадрате	Готовый выпуск*Прибыль
А	1	2	3	4	5
	x	y	X2	Y2	X*y
1	1,4	43,1	1,96	1857,61	60,34
2	1,7	52,5	2,89	2756,25	89,25
3	1,8	55,6	3,24	3091,36	100,08
4	1,9	58,8	3,61	3457,44	111,72
5	2	61,9	4	3831,61	123,8
6	1,9	58,8	3,61	3457,44	111,72
7	1,8	55,6	3,24	3091,36	100,08
8	1,7	52,5	2,89	2756,25	89,25
9	1,4	43,1	1,96	1857,61	60,34
10	1	30,6	1	936,36	30,6
11	1,5	44,2	2,25	1953,64	66,3
12	1,7	52,5	2,89	2756,25	89,25
13	1,8	54,8	3,24	3003,04	98,64
14	1,9	58,6	3,61	3433,96	111,34
15	2	61,9	4	3831,61	123,8
16	1,9	54,5	3,61	2970,25	103,55
17	1,8	51,5	3,24	2652,25	92,7
18	1,7	48,6	2,89	2361,96	82,62
19	1,2	35	1,44	1225	42
20	1,4	38,4	1,96	1474,56	53,76
Итого:	33,5	1012,5	57,53	52755,8	1741,14

Уравнение тренда принимает вид:

y=-2,789+31,889x.

Вычислим коэффициент корреляции по формуле:

.

Построим график корреляционной зависимости и изобразим линию тренда:

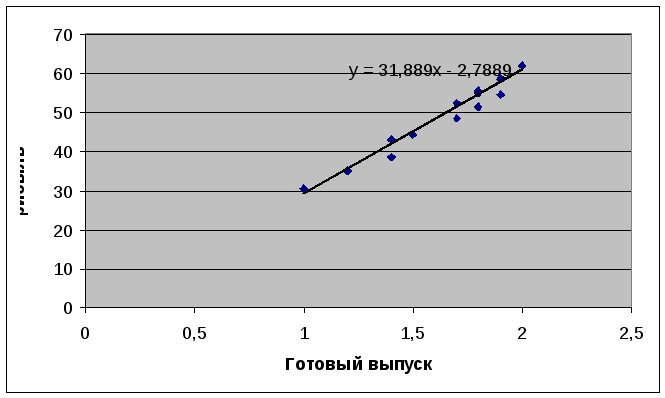
Рисунок 1 – График корреляционной зависимости.

Вывод:так какr_xy=0,981, то между переменнымиyиxсуществует достаточно тесная линейная зависимость, которая может быть отражена с помощью уравнения регрессииy=-2,789+31,889x.

Коэффициент а₁=31,889 характеризует размер прироста суммы прибыли, обусловленной приростом объема готового выпуска продукции на тысячу рублей.

Уравнение y=-2,789+31,889xхарактеризует среднюю сумму прибыли в зависимости от объема готового выпуска. Слово «среднее» выражает здесь тот факт, что реальное значение суммы затратy, соответствующее некоторому реальному готовому выпускуx, будет находиться в некоторой окрестности значенияy=-2,789+31,889x.