5.2.1 В кожний момент часу геометрична сума всіх ________ сил, що діють на рухому матеріальну точку, і умовно прикладеної сили інерції дорівнює нулеві.

в) – “активних і пасивних”;

5.2.2 Вкажіть правильний вираз

принципу Д’Аламбера для матеріальної точки під дією активних і пасивнихсил.

а) ;

5.2.3 В кожний момент часу головний вектор і головний момент відносно деякого нерухомого центра всіх ________ сил, що діють на систему, і умовно прикладених до її точок сил інерції відповідно дорівнюють нулеві.

а) – “зовнішніх”;

5.2.4 Вкажіть правильні вирази принципу Д’Аламбера для механічної системи під дією зовнішніх , внутрішніхі пасивнихсил.

В)5.2.5 Вкажіть правильні вирази принципу Д’Аламбера для механічної системи під дією зовнішніх , внутрішніхі пасивнихсил.

б) 5.3.1.1 Вкажіть правильний вираз залежності загального рівняння в’язі, щоб рух системи був можливим.

а) 5.3.1.2 Вкажіть правильний вираз залежності утримуючої або двохсторонньої в’язі.

б) ;

5.3.1.3 Вкажіть правильний вираз залежності стаціонарної склерономної в’язі.

а) ;

5.3.1.4 Вкажіть правильний вираз залежності нестаціонарної реономної в’язі.

в) ;

15.3.1.5 Вкажіть правильний вираз залежності геометричної в’язі.

б) ;

5.3.1.6 Вкажіть правильний вираз залежності кінематичної в’язі.

а) ;

5.3.1.7 _________ в’язі утворюють клас голономних в’язей.

а) – “кінематично-інтегруючі і геометричні”;

5.3.1.8 Якщо в рівнянні ___________ можна виключити швидкості точок, то в’язь називають не голономною.

б) – “кінематичної в’язі шляхом інтегрування не”;

5.3.2.1 Можливим переміщенням матеріальної системи називають______ мале переміщення системи, яке допускається накладеними на систему в’язями в даний момент часу.

б) – “уявне нескінченно”;

5.3.2.2 Можливим переміщенням матеріальної системи називають уявне нескінченно мале переміщення системи, яке допускається накладеними на систему __________ в даний момент часу.

а) – “в’язями”;

5.3.2.3 Дійсні елементарні переміщення здійснюються за _______________ часу і визначаються накладеними в’язями та діючими на систему силами.

в) – “нескінченно малий проміжок”;

5.3.2.4 Дійсні елементарні переміщення здійснюються за нескінченно малий проміжок часу і визначаються ________ на систему.

а) – “накладеними в’язями та діючими силами”;

5.3.2.5 Можливі переміщення уявно здійснюються за нескінченно малий проміжок часу і визначаються ________ на систему.

а) – “тільки накладеними в’язями”;

5.3.2.6 Вкажіть правильний рисунок можливих переміщень тіла К.

а)

5.3.2.7 Вкажіть правильний рисунок утримуючої в’язі.

а)

5.3.2.8 Дійсне переміщення матеріального об’єкта співпадає з можливим його переміщенням тільки у випадку, коли на об’єкт накладені ___________ в’язі.

б) – “стаціонарні”;

5.3.2.9 Числом степенів вільн

сті системи називають число __________ переміщень.

в) – “незалежних її можливих”;

5.3.2.10 Число степенів вільності системи з двохсторонніми голономними в’язями визначається кількістю _________ координат, які однозначно визначають положення точок системи в просторі.

г) – “незалежних”;

5.3.2.11 Вкажіть правильну формулу кількості степеней вільності (S) рухомої системи n матеріальних точок, обмеженої тільки голономними двохсторонніми (d) в’язями.

б) ;

5.3.2.12 В’язі називають ідеальними, якщо сума робіт всіх __________ на будь-якому можливому переміщенні системи, дорівнює нулеві.

б) – “реакцій в’язей”;

5.3.2.13 Вкажіть правильний вираз ідеальних в’язей системи, на яку діють активні сили , реакцій в’язейі, яка може отримати можливета дійснепереміщення.

г) ;

5.3.3.1 Для рівноваги механічної системи з двосторонніми, ідеальними, стаціонарними в’язями необхідно і достатньо, щоб алгебраїчна сума робіт всіх _______ сил, що діють на систему, на будь-якому з її можливих переміщень дорівнювала нулеві.

б) – “активних”;

5.3.3.2 Вкажіть правильний вираз принципу можливих переміщень (загального рівняння статики).

б) ;

5..3.3.3 Вкажіть правильний вираз принципу можливих переміщень (загального рівняння статики) в аналітичній формі.

а) ;

5.3.3.4 Вкажіть правильний вираз принципу можливих переміщень (загального рівняння статики) в аналітичній формі.

в) ;

5.4.1 Для рухомої механічної системи, на яку накладені утримуючі стаціонарні ідеальні в’язі, алгебраїчна сума робіт всіх _______ на будь-якому можливому переміщенні системи дорівнює нулеві.

в) – “активних сил, що діють на систему, і умовно прикладених сил інерції”;

5.4.2 Вкажіть правильний вираз принципу Д’Аламбера -Лагранжа (загального рівняння динаміки).

в) ;

5.4.3 Вкажіть правильний вираз принципу Д’Аламбера -Лагранжа (загального рівняння динаміки).

б) ;

5.4.4 Вкажіть правильний вираз принципу Д’Аламбера -Лагранжа (загального рівняння динаміки) в аналітичній формі.

а) 5.4.5 Вкажіть правильний вираз принципу Д’Аламбера -Лагранжа (загального рівняння динаміки) в аналітичній формі.

б)

6.1.1 Узагальненими координатами називають сукупність ________, які однозначно визначають положення матеріальної системи в просторі.

б) – “незалежних між собою параметрів”;

6.1.2 Узагальненою швидкістю називають ­­­­__________ від узагальненої координати.

а) – “першу похідну за часом”;

6.1.3 Вкажіть правильний вираз узагальненої швидкості.

б) ;

6.1.4 Узагальненим пришвидшенням називають ______ від узагальненої координати.

а) – “другу похідну за часом”;

6.1.5 Вкажіть правильний вираз узагальненого пришвид-шення.

в) ;

6.1.6 Одиниці вимірювання узагальненої швидкості і узагальненого пришвидшення визначаються одиницею вимірювання ________ координати.

в) – “узагальненої”;

6.1.7 Вкажіть правильний вираз швидкості точок системи для і-ї точки системи для реономної системи (системи з S нестаціонарними в’язями ) .

б) ;

6.1.8 Вкажіть правильний вираз швидкості і-ї точки системи для склерономної системи (системи з S стаціонарними в’язями ).

б) ;

6.2.1 Вкажіть правильний вираз тотожностей Лагранжа.

а)

6.3.1 Простором конфігурацій (координатним простором) називають __________ S-вимірний простір, координатами якого є узагальнені координати .

в) – “декартовий”;

6.3.2 Фазовим простором (простором стану) називають 2S-мірний декартовий простір, координатами якого є узагальнені ____________ .

а) – “координати і узагальнені швидкості ”;

6.3.3 ____________ фазовий простір називають фазовою площиною.

а) – “двовимірний”;

6.3.4 При русі системи зображуюча точка у фазовому просторі описує деяку лінію, яку називають ___________.

в) – “фазовою траєкторією”;

6.3.5 Сукупність фазових траєкторій називають ______________ системи .

а) – “фазовим портретом”;

6.4.1 Відношення _________ на можливих переміщеннях, викликаних можливим приростом узагальненої координати q_к, до цього приросту q_к називають узагальненою силою Q_k, що відповідає узагальненій координати q_k.

а) – “роботи сил системи, виконаної”;

6.4.2 Вкажіть правильний вираз узагальненої сили Q_k (S – кількість узагальнених координат, , ).

а) ;

6.4.3 Вкажіть правильний вираз узагальненої сили Q_k (S – кількість узагальнених координат).

б)

6.4.4 Узагальнена сила є _______________ величиною.

б) – “скалярною”;

6.4.5 Узагальнені сили _______узагальнених координат.

а) – “залежать від вибору”;

6.4.6 Кількість узагальнених сил __________ кількості узагальнених координат, за допомогою яких визначають положення механічної системи в просторі.

б) – “дорівнює”;

6.4.7 Кількість узагальнених сил ___________ кількості степеней вільності механічної системи.

в) – “дорівнює”;

6.4.8 Одиниця вимірювання узагальненої сили ________ одиницею вимірювання узагальненої ____________.

а) – “визначається … координати”;

6.4.9 Чи може узагальнена сила мати одиницю вимірювання .

а) – “може, якщо узагальненою координатою є кут повороту ”;

6.4.10 Вкажіть правильну формулу можливої роботи сил системи на можливих переміщеннях, обчислену через узагальнені сили (де S – кількість узагальнених координат, ).

б) ;

6.4.11 Вкажіть правильний вираз узагальненої сили Q_k, ().

б) ;

6.4.12 Вкажіть правильний вираз узагальненої сили Q_k, якщо відомі проекції сили на декартові осі координатиХ_і, У_і, Z_i (де S – кількість узагальнених координат, ).

в) 6.4.13 Вкажіть правильний вираз узагальненої сили Q_k, якщо відомі проекції сил потенціального поля (S – кількість узагальнених координат, ).

б) 6.4.14 Вкажіть правильний вираз узагальненої силиQ_k, якщо відома потенціальна енергія системи.

в) ;

6.5.1 Необхідною і достатньою умовою рівноваги меха-нічної системи, на яку накладені утримуючі ідеальні голономні в’язі, є рівність нулеві всіх її ___________.

а) – “узагальнених сил”;

6.5.2 Вкажіть правильний вираз умови рівноваги механічної системи в узагальнених силах.

в) ;

6.5.3 У положенні рівноваги консервативна система, на яку накладені ______________ в’язі, має екстремальне значення потенціальної енергії.

в) – “утримуючі ідеальні голономні;

6.5.4 Вкажіть правильний вираз умови при якій потенціальна енергія має екстремальне значення.

а) ;

6.6.1 Вкажіть правильний вираз диференціальних рівнянь руху голономних механічних систем в узагальнених координатах (рівняння Лагранжа другого роду).

д)

.6.6.2 Вкажіть правильний вираз диференціальних рівнянь руху голономних механічних систем в узагальнених координатах (рівняння Лагранжа другого роду).

г) 6.6.3 Вираз__________в теоретичній механіці називають функцією Лагранжа (L), або кінетичним потенціалом.

в) ;

6.6.4 Вкажіть правильний вираз диференціальних рівнянь руху (рівняння Лагранжа другого роду) для консервативної системи.д) .

6.6.5 Вкажіть правильний вираз рівнянь Лагранжа другого роду для консервативної системи. д) .

6.6.6 Вкажіть правильний вираз диференціальних рівнянь руху голономних механічних систем в узагальнених координатах (рівняння Лагранжа другого роду).

в) 6.6.7 Якщо функція Лагранжа явно не залежить від деякої ___________, то таку узагальнену координату називають циклічною.

а) – “узагальненої координати ”;

6.6.8 Вкажіть правильний вираз рівняння Лагранжа другого роду для консервативної системи, яке відповідає циклічній координаті q_j.

б) ;

6.6.9 Вкажіть правильний вираз, який відповідає узагальненому імпульсу.

в) ;

6.6.10 Узагальнений імпульс циклічної координати______.

б) – “величина стала”;

6.6.11 Кінетична енергія склерономної механічної системи є функцією другого степеня від узагальнених _________ і виражається однорідною їх квадратичною формою.

а) – “швидкостей”;

6.6.12 Вкажіть правильний вираз кінетичної енергії системи в узагальнених координатах (S – кількість узагальнених координат, , - циклічна координ

а) 6.7.1 Сили, що спричиняють ___________ енергії системи, називають дисипативними.

б) – “розсіювання механічної”;

6.7.2 Вкажіть правильний вираз дисипативної функції Релея, якщо коефіцієнт n пропорційності дорівнює .

б) ;

6.7.3 Вкажіть правильний вираз узагальненої сили дисипативних сил , якщо відома дисипативна функція РелеяR.

в) .

6.7.4 Вкажіть правильний вираз дисипативної функції Релея для склерономної системи в узагальнених координатах (- коефіцієнт опору середовища, - циклічна координата, - узагальнена координата).

в) 6.7.5 Швидкість зменшення повної механічної енергії системи дорівнює _________ функції Релея.

а) – “подвійній”;

6.7.6 Вкажіть правильний вираз, який зв’язує функцію Релея і швидкість зміни повної механічної енергії.

б) ;

6.7.7 Узагальнені сили механічної системи загалом можна представити у вигляді, де :

в) , 6.7.8 Вкажіть правильний вираз рівняння Лагранжа другого роду з врахуванням функції Релея (де 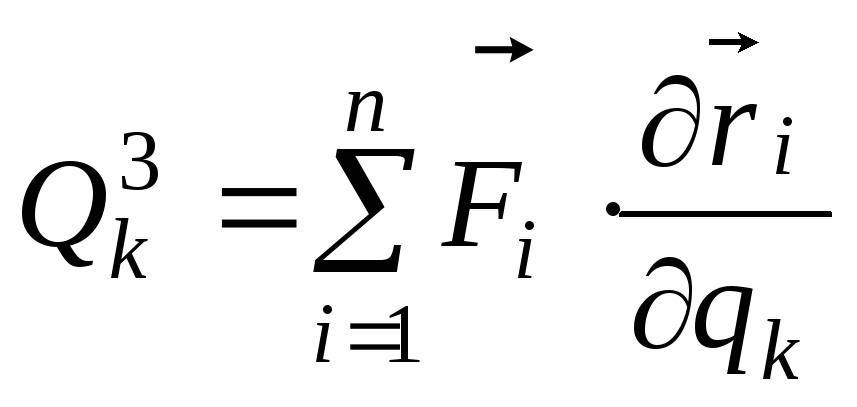) а)

93