
n1
.pdf
|
|
(R + R + R )I |
11 |
- R I |
22 |
- R I |
33 |
= E - E |
;ü |
|
|||||||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
1 |
2 |
ï |
|
|
|
|
|
|||||||||||||||||
|
|
(R2 + R3 + R5 )I22 - R2 I11 - R5 I33 = E2; |
|
|
|
ý |
(2.3) |
||||||||||||||||||||||||||||||||||||||||
|
|
(R4 + R5 + R6 )I33 - R4 I11 - R5 I22 = 0. |
|
|
|
|
ï |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
þ |
|
||||||||||||||||||||||||||||||||||||||||
Приведём систему (2.3) к стандартному виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
(R1 + R2 + R3 )I11 - R2 I22 - R4 I33 = E1 - E2 |
;ü |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
- R |
I |
11 |
+ (R + R |
+ R |
)I |
22 |
- R |
|
I |
33 |
|
= E ; |
ï |
|
|
|
|
(2.4) |
|||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
2 |
|
|
ý |
|
||||||||||||||||||
|
|
- R4 I11 - R5 I22 + (R4 + R5 + R6 )I33 = 0. |
|
|
|
ï |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
þ |
|
|||||||||||||||||||||||||||||||||||||||||
Обозначим R1 + R2 + R3 = R11, |
|
R2 + R3 + R5 = R22 , |
R4 + R5 + R6 = R33, |
||||||||||||||||||||||||||||||||||||||||||||
R12 = R21 = −R2, R13 = R31 = −R4 , R23 = R32 = −R5 , |
E11 = E1 − E2 , |
|
|||||||||||||||||||||||||||||||||||||||||||||
E22 = E2 , E33 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда в более общем виде система (2.4) запишется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
R I |
11 |
+ R I |
22 |
+ R I |
33 |
|
|
= E ; |
ü |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
11 |
|
|
12 |
|
|
|
|
|
13 |
|
|
|
|
|
|
11 |
|
ï |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
R21 I11 + R22 I22 + R23 I33 = E22; |
ý |
|
|
|
|
|
(2.5) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
R I |
11 |
+ R I |
22 |
+ R I |
33 |
|
= E |
33 |
. |
ï |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
31 |
|
|
32 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|||||||||||||||||||
или в матричной форме R I = E , |
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
R11 |
R12 |
|
R13 |
|
|
|
|
|
|
|
|
I11 |
|
|
|
|
|
|
|
|
|
E11 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
R = |
R21 R22 R23 |
, I = |
|
I22 |
|
, E = |
|
E22 |
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
R31 R32 R33 |
|
|
|
|
|
|
|
I33 |
|
|
|
|
|
|
|
|
|
E33 |
|
|
|
|
|
|
|
|
||||||||||||||||||
Запишем формулы для расчёта контурных токов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
I11 = |
11 |
, |
I22 = |
|
|
|
|
22 |
, I33 = |
|
|
33 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
R11 |
R12 |
|
|
R13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E11 |
|
|
R12 |
|
|
R13 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
D = |
R21 |
R22 |
|
|
R23 |
, |
|
|
|
|
|
|
|
D11 = |
E22 |
|
|
R22 |
|
|
R23 |
|
, |
|
|||||||||||||||||||||||
|
R31 |
R32 |
|
|
R33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E33 |
|
|
R32 |
|
|
R33 |
|
|
|
|||||||||||||||
|
|
R11 |
|
E11 |
R13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R11 |
|
R12 |
|
|
E11 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
D22 = |
R21 |
|
E22 |
R23 |
, |
|
|
|
|
|
|
D33 = |
R21 |
|
R22 |
|
|
E22 |
|
. |
|
||||||||||||||||||||||||||
|
|
R31 |
|
E33 |
R33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R31 |
|
R32 |
|
|
E33 |
|
|
|
||||||||||||||||||
Решение в матричной форме I = R−1E = |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
11

Подставим в (2.5) величины заданных сопротивлений и эдс
50 I11 − 15 I22 − 25 I33 = −100;
-15 I11 + 65 I22 - 30 I33 = 200;
-25 I11 - 30 I22 + 90 I33 = 0.
Решим полученную систему на ЭВМ или ручным способом путём расчёта определителей , 11, 22, 33 по формулам Крамера.
Получим I11 = −0,4570 А, I22 = 3,4425 А, I33 = 1,0206 А.
4. Выразим токи в ветвях через контурные. Направления токов в ветвях выберем такими же как и в предыдущем примере (см. рис. 2.2).
Тогда получим
I1 = I11 = −0,4570 А,
I2 |
= I11 |
− I22 = −0,4570 − 3,4425 = −3,8995 А, |
I3 |
= −I22 = −3,4425 А, |
|
I4 |
= I33 |
− I11 = 1,0206 + 0,4570 = 1,4776 А, |
I5 |
= I33 |
− I22 = 1,0206 − 3,4425 = −2,4219 А, |
I6 |
= I33 |
= 1,0206 А. |
Отметим, что при определении токов I2 , I4 и I5 учитывалось, что контур-
ный ток, совпадающий с током в ветви, берётся со знаком «+», не совпадающий
– со знаком «–». При этом значения контурных токов подставляются в формулы со своим знаком.
Правильность расчёта проверим по балансу мощностей. Мощность источников тока определим по формуле, составленной согласно схеме на рис. 2.2.
Pи = Е1I1 − Е2I2 = 100(− 0,4570)− 200(− 3,8995) = 734,2 Вт.
Мощность потребителей (нагрузок) найдём по формуле
6
Рн = å Rk Ik2 = 10(− 0,4570)2 + 15(− 3,8995)2 + 20(− 3,4425)2 +
k =1
+ 25(1,4775)2 + 30(− 2,4219)2 + 35(1,0206)2 = 734,1961 Вт.
Относительная ошибка δ должна быть меньше наперёд заданного числа, например, 5 %:
d = Ри - Рн 100% = 5,24 ×10-4 % < 5% .
Ри
12

Вопросы для самопроверки
1.В чём заключается сущность метода расчёта сложных электрических цепей по законам Кирхгофа?
2.Чему равно число уравнений, составляемых по 1-му закону Кирхгофа?
3.Чему равно число уравнений, составляемых по 2-му закону Кирхгофа?
4.Каким методом математически можно решать систему уравнений, составленную по законам Кирхгофа?
5.В чём заключается сущность метода контурных токов?
6.Чему равно число уравнений в этом методе расчёта?
7.Каким методом математически можно решать систему уравнений, составленную по неизвестным контурным токам?
8.Как проверить правильность расчёта сложных электрических цепей?
9.Чему равна мощность источников эдс?
10.Чему равна мощность потребителей (нагрузок)?
ЛЕКЦИЯ № 3 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Вэлектротехнике переменный ток применяется более широко, чем постоянный. Это связано с возможностью легко преобразовать его для передачи на расстояние и потребления в народном хозяйстве.
Переменным током называют ток, который изменяется во времени по величине и направлению. Чаще всего переменный ток в электротехнике может быть однофазным и трёхфазным.
3.1.Переменный однофазный синусоидальный ток
Втехнике широко используются процессы, изменяющиеся по периодическому закону.
Однофазный синусоидальный ток представляет собой переменный ток, изменяющийся во времени по периодическому закону, каковым является синусоидальный закон (его называют ещё гармонический закон). График его представлен в виде колебательного процесса на рис. 3.1.
i, A |
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
0 |
1 |
Т |
1Т |
3 |
Т |
I |
Т |
t,с |
|
4 |
|
2 |
4 |
|
|
m |
|
|
|
|
Т |
|
|
|
|
|
Рис. 3.1. Волновая диаграмма однофазного синусоидального тока |
||||||||
13

В таком процессе мгновенные значения тока повторяются через равные промежутки времени Т. В этом случае закон изменения синусоидального тока выражается функцией вида
i = Im sin(t + kT ),
где i – мгновенное значение тока, т. е. значение тока в данный момент времени; Im – максимальное значение тока, называемое амплитудой; Т – период колеба-
ния тока, т. е. интервал времени в секундах (с), за которое совершается одно полное колебание; k – любое целое число.
На основе понятия периода Т вводится понятие частоты f, 1с ,
f = |
1 |
. |
(3.1) |
|
|||
|
T |
|
|
Частота – это число периодов колебаний какого либо процесса (тока, напря-
жение и др.) за одну секунду. Измеряется частота в герцах (Гц). Итак 1 Гц = c1 .
Втеории электротехники ось времени (ось аргумента) часто представляют не
всекундах (единица времени), а в углах. Для их измерения используют безразмерную радианную величину.
Радиан есть мера измерения угла поворота единичного радиуса (r = 1) круга. В то же время круг является одним полным колебанием (периодом) какого-либо процесса.
Вгеометрии радиан – это центральный угол α для дуги, длина l которой
равна радиусу r, т. е. при r = l α = 1 радиан (рад). При этом величина центрального угла α в произвольном круге определяется как отношение длины дуги l, на которую этот угол опирается, к радиусу r , т. е. α = l / r . В круге с радиусом r = 1 (единичном круге) радианная мера угла равна длине дуги, которую вырезают стороны этого угла, т. е. α = l/ r = l/1= l. Полный поворот радиуса в круге будет равен центральному углу α в 3600, опирающемуся на дугу, равную длине L всей ок-
ДL , где L - длина ок-
ружности любого круга, а Д - диаметр этого круга, равный 2 r. Отсюда в единичном круге при r = 1 L = 2π = 6,28, а следовательно и α = L = 6,28. В результате, радианная мера полного центрального угла α равна 2π = 6,28 рад., Таким образом, α = 1 рад. = 3600 / 6,28 = 57017/45// (примерно 1/6 часть круга). Существуют формулы перехода от градусной меры в радианную и наоборот:
αрад = α ° × π  180° и α ° = αрад ×180°
180° и α ° = αрад ×180°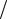 π .
π .
Рассмотрим более подробно физический смысл колебания, представленного на рис. 3.2.
Известно, что одно полное колебание какого-либо процесса можно представить в виде одного оборота радиуса-вектора om на угол 3600, т. е. на один круг. В то же время в круг можно поместить прямоугольный треугольник оnk с гипотенузой с, равной радиусу r круга, и его вершиной о в центре круга.
14

′ |
p |
|
|
|
p |
|
|
|
|
|
|
n |
|
n |
′ |
|
|
|
|
n |
|
r |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
= |
a |
|
|
|
|
|
|
|
α |
|
m |
′ |
|
m |
α |
||
|
|
m |
|
||||||
|
|
|
к |
|
0 |
|
|
||
0 |
|
b |
|
0 |
π = 180° |
|
π = 360° |
|
|
|
|
|
|
|
|||||
′′ |
|
|
′′′ |
|
|
′′ |
|
′′′ |
|
n |
|
′ |
|
|
′ |
|
|||
|
|
n |
|
|
n |
n |
|
||
|
p |
|
|
|
|
p |
|
|
|
Рис. 3.2. Определение физического смысла колебательного процесса |
|
||||||||
На рис. 3.2 a и b – катеты прямоугольного прямоугольника оnk; с – гипотенуза треугольника, равная радиусу круга; α – центральный угол, образованный катетом b и гипотенузой c; mn – дуга, на которую опирается центральный угол α .
Следовательно, если прямоугольный треугольник расположен в окружности с радиусом, равным его гипотенузе так, что одна из его вершин находится в центре круга, то синусоидальная функция угла является тригонометрической круговой функцией, т. е. функцией центрального угла α , заключённого между прилежащим катетом и гипотенузой прямоугольного треугольника.
Таким образом, одно полное колебание какого-либо процесса (тока, напряжения и т. д.) будет равно повороту центрального угла в 2π радиан, или иначе будет происходить за 2π секунд.
В теоретической электротехнике вводится понятие круговой или циклической частоты ω, рад/с, которая понимается как угловая скорость вращения радиусавектора. Она равна углу α поворота радиуса-вектора в единицу времени t . За один полный поворот (один круг) в 2π радиан радиус-вектор будет иметь один период вращения продолжительностью T секунд
ω = |
α |
= |
2π |
= 2π f . |
(3.2) |
|
t |
T |
|||||
|
|
|
|
Итак, круговая частота переменного тока, рад/с, – это число периодов колебания тока за 2π секунд.
В результате введения понятия круговой частоты ω график синусоидального тока в виде волновой диаграммы (см. рис. 3.3) можно изобразить через радианное измерение аргумента (независимой переменной величины).
i |
|
|
|
|
|
|
|
Im |
1 |
|
|
T |
|
|
π |
2T |
3 |
|
ωt |
|
0 |
π |
π |
2π |
|||
|
|
|||||
|
2 |
|
2 |
|
Im |
|
|
|
Т = 2π |
|
|
|
|
i |
|
|
|
Im |
1 |
T |
|
0 |
2T |
ωt |
|
π |
2π |
||
|
|
Im |
|
ψ |
Т = 2π |
|
|
Рис. 3.3. График синусоидального тока в виде волновой диаграммы
15

В этом случае закон изменения синусоидального тока выражается функцией вида: i = Im sinωt – для рис. 3.3, а (y = 0 );
i = Im sin(ωt + ψ) – для рис. 3.3, б (y ¹ 0).
Анализируя выражения представленных на рис. 3.3 а и б функций, вводим понятия:
1) фаза или аргумент синуса – величина (ωt + ψ). Фаза характеризует состоя-
ние колебания, т. е. она даёт возможность определить численное значение величины колебания процесса в данный момент времени t ;
2) значение фазы при t = 0, когда wt + y = w×0 + y = y , называется начальной фазой и обозначается ψ .
При радианном измерении аргумента синуса ωt в течение времени Т фаза тока увеличивается на 2π . Поэтому круговая частота ω показывает на сколько радиан изменится фаза тока за 1 с.
Например, при частоте f =1 Гц фаза тока изменится на
w = 2p f = 6,28 ×1= 6,28 рад/с, а при f = 50 Гц на w = 6,28×50 = 314 рад/с.
Таким образом, любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
3.2. Характеристики синусоидальных величин
3.2.1. Действующее значение синусоидально изменяющейся величины переменного тока и напряжения
Кроме понятий мгновенного и максимального значений тока и напряжения, существует понятие их действующего значения.
Например, действующее значение I синусоидального тока i = Im sinωt чис-
ленно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет на сопротивлении R такое же количество теплоты, что и синусоидальный ток.
Действующее значение тока ещё называют эффективным или среднеквадратичным. Его определяют из выражения
|
1 T |
2 |
|
= |
|
1 |
2π |
2 |
2 ω ω |
= |
I |
m |
|
= |
|
. |
|
I = |
|
òi |
dt |
|
ò |
Im sin |
|
|
|
0,707 Im |
|||||||
|
T |
0 |
|
|
|
|
2π 0 |
|
|
2 |
|
|
|
||||
Аналогично определяют действующее значение напряжения
U= U2m = 0,707Um .
3.2.2.Среднее значение синусоидально изменяющейся величины переменного тока и напряжения
Под средним значением синусоидального переменного тока понимают среднее его значение за полпериода и определяют из выражения
|
|
T |
1 |
π |
2 |
|
|||
|
1 |
|
2 |
|
|
||||
Iср = |
|
òidt = |
ò Im sinωt dωt = |
Im = 0,638Im . |
|||||
|
π |
|
|||||||
T |
|||||||||
|
0 |
|
0 |
π |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
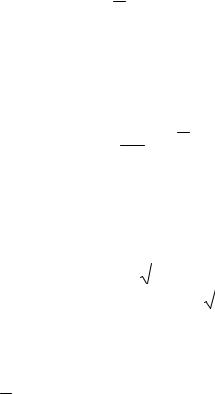
Аналогично определяется среднее значение переменного напряжения
Uср = 2πUm = 0,638 Um .
3.2.3. Коэффициент амплитуды и формы
Коэффициент амплитуды представляет собой отношение амплитуды периодически изменяющейся функции к её действующему значению.
Так, для синусоидального тока
Ka = IIm = 
 2 =1,41.
2 =1,41.
Коэффициент формы – это отношение действующего значения периодически изменяющейся функции к её среднему значению за полпериода.
Так, для синусоидального тока
|
I |
|
|
Im |
|
π |
|
|
|
|||
Kф = |
= |
|
|
2 |
|
= |
|
|
=1,11. |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
2 |
|||||
|
Iср |
2Im |
|
|
|
|||||||
π
Коэффициенты амплитуды Ka и формы Kф для несинусоидальных периодических токов и напряжений будут не равны своим значениям для синусоидальной функции, т.е. Ka ¹ 
 2 =1,41 и Kф ¹1,11. Отличие Ka от 1,41 и Kф от 1,11 по-
2 =1,41 и Kф ¹1,11. Отличие Ka от 1,41 и Kф от 1,11 по-
зволяет судить о том, насколько несинусоидальный ток или напряжение отличается (искажается) от синусоидального.
Вопросы для самопроверки
1.Что называется переменным током?
2.Что называется периодом переменного тока?
3.Что называется частотой переменного тока и в каких единицах она измеряется?
4.Что такое угловая или циклическая частота переменного тока и в каких единицах она измеряется?
5.Что такое фаза переменного тока?
6.Что такое начальная фаза переменного тока?
7.Что называется амплитудным и мгновенным значением переменного тока?
8.Что называется действующим значением переменного тока?
9.Что называется средним значением переменного тока?
10.Как определяется коэффициент амплитуды переменного тока?
11.Как определяется коэффициент формы переменного тока?
ЛЕКЦИЯ № 4
СПОСОБЫ ЗАДАНИЯ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА И ЗАКОНЫ КИРХГОФА В ЕГО ЦЕПЯХ
Синусоидальный ток можно задать тремя различными формами:
1)математическим уравнением,
2)волновой диаграммой,
17

3) вращающимся вектором. |
|
|
||
4.1. Представление переменного синусоидального тока математическим |
||||
уравнением |
|
|
|
|
|
Закон изменения синусоидального тока выражается функцией вида |
|||
|
|
|
i = Im sin(ωt + ψ), |
|
|
Это уравнение определяет мгновенное значение тока, т.е. значение тока в лю- |
|||
бой момент времени. |
|
|
||
4.2. Представление переменного синусоидального тока вращающимся векто- |
||||
ром. Векторные диаграммы |
|
|||
|
Пусть в прямоугольной системе координат х и у имеется вектор длиной Im , |
|||
расположенный под углом ψ к горизонтальной оси (рис. 4.1). |
||||
Заставим этот вектор вращаться против часовой стрелки с угловой скоростью |
||||
y |
|
|
ω. Тогда за время t он повернётся на угол |
|
|
|
ωt . Проекцию вращающегося вектора на |
||
|
a |
b |
|
|
|
ω |
вертикальную ось обозначим через функ- |
||
|
ωt+ψ |
Im |
цию i = Im sin(ωt + ψ). Функция i пред- |
|
|
|
|||
i |
|
|
|
ставляет собой мгновенное значение тока. |
ωt |
|
Im |
Изображение тока с помощью вектора |
|
|
|
называется его векторной диаграммой. |
||
|
ψ |
|
|
|
|
|
|
Длина вектора может быть равна ампли- |
|
|
0 |
|
|
|
|
|
x |
тудному значению Im , либо действитель- |
|
|
Рис. 4.1. Вращающийся вектор |
ному значению I . Обычно вектор при |
||
|
|
|
|
этом показывается не в произвольный мо- |
|
|
|
|
мент времени t , а в начальный, когда |
|
|
|
|
t = 0 , т. е. угол наклона вектора к горизон- |
|
|
|
|
тальной оси равен начальной фазе. |
|
|
|
|
Построим векторную диаграмму двух |
|
|
|
|
векторов – тока и напряжения, представ- |
|
|
|
|
ленную на рис. 4.2. |
|
|
|
|
Длины векторов равны действующим |
|
|
|
|
значениям тока и напряжения, углы их на- |
Рис. 4.2. Векторная диаграмма напряже- |
клона к горизонтальной оси – начальным |
|||
фазам, а угол между векторами, равный раз- |
||||
ния и тока |
|
|
ности начальных фаз ψu и ψi , определяет |
|
|
|
|
|
|
|
|
|
|
сдвиг фаз ϕ напряжения и тока |
|
|
|
|
ϕ = ψu - ψi . |
|
На диаграмме стрелка, показывающая угол ϕ, всегда изображается в положи- |
|||
тельном направлении – против часовой стрелки. |
||||
|
Векторная диаграмма даёт наглядное представление об отставании одних ве- |
|||
личин и опережении других. Если начальные фазы U и I (ψu и ψi ) равны нулю, |
||||
то можно изображать векторную диаграмму без осей и располагать её как удобно. |
||||
18

4.3. Представление переменного синусоидального тока волновой диаграммой
График синусоидального тока можно изобразить в виде волновой диаграммы, представленный на рис. 4.3.
На волновой диаграмме указана начальная фаза, которая определяется углом ψ, измеряемым от ближайшей к началу координат точки перехода синусоиды через ноль до точки начала координат. Начальная фаза ψ положительна в тех случаях, когда начало синусоиды смещено от точки ноль (начало координат) влево и наоборот – отрицательна, когда смещена вправо.
i 
Im
0 |
π |
2 |
|
t |
|
π ω |
|||||
ψ
Рис. 4.3. Волновая диаграмма синусоидального тока
Примеры перехода от одной формы задания к другой:
i = 10sin(ωt + 45°), ψi < 0. |
i |
|
Im =10 |
0 |
π |
2π ωt |
ψ
45° 135°
4.4. Законы Кирхгофа в цепях синусоидального тока и методы расчёта этих цепей
Для мгновенных значений эдс, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
Первый закон Кирхгофа: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю
n |
|
åik (t) = 0 , |
(4.1) |
k =1 |
|
где n – число ветвей, сходящихся в узле.
Второй закон Кирхгофа: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме напряжений на всех остальных элементах контура
19
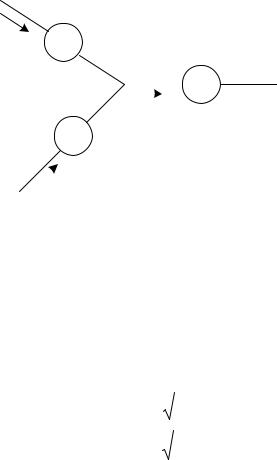
m |
m |
|
åek (t) = |
åuk (t), |
(4.2) |
k =1 |
k =1 |
|
где m – число ветвей, образующих контур.
Токи, напряжения и эдс, входящие в уравнения (4.1) и (4.2), есть синусоидальные функции времени, которые рассматриваются как проекции определённых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записать как для действующих, так и для амплитудных значений.
Законы Кирхгофа в векторной форме
n |
|
|
m |
|
m |
|
|
|
å I |
k = 0; |
å |
E |
k = å |
U |
k . |
(4.3) |
|
k =1 |
k =1 |
k =1 |
|
|||||
Следовательно, возможны два способа расчёта цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (4.1) и (4.2) и применение метода векторных диаграмм, основанного на уравнениях (4.3).
Рассмотрим применение первого закона Кирхгофа для решения цепей синусоидального тока.
4.4.1. Применение метода расчёта непосредственно над синусоидальными функциями
i1 А1

 А3 i3
А3 i3
А2
 i2
i2
Рис. 4.4. Узел электрической цепи
Пример.
В узле электрической цепи (рис. 4.4) сходятся три ветви.
Даны токи, А, двух ветвей:
i1 = 8sin(ωt + 30°), i2 = 6sin(ωt +120°).
Требуется записать выражение тока i3 и определить показания амперметров
электромагнитной системы.
Решение. |
i1 + i2 − i3 = 0 , |
1-й закон Кирхгофа для узла электрической цепи запишем как |
|
отсюда i3 = i1 + i2 , в результате |
|
i3 = 8sin(ωt + 30°)+ 6sin(ωt +120°) = I3m sin(ωt + ψ3 )Сумма |
двух синусоид |
одинаковой частоты есть тоже синусоида той же частоты. Её амплитуда и начальная фаза могут быть найдены по известным из математики формулам:
|
|
|
|
|
= |
|
||||||
|
|
I3m = |
I12m + I22m + 2 × I1m × I2m × cos(y1 - y2 ) |
|
||||||||
|
|
|
|
= 10 A, |
|
|||||||
|
|
= |
82 + 62 + 2 ×8 × 6 × cos(30° -120°) |
|
||||||||
tgy3 |
= |
I1m sinψ1 |
+ I2m sinψ2 |
= |
8 × sin30° + |
6 |
× sin120° |
= 2,341, |
||||
I1m cos y1 |
+ I2m cos y2 |
8 × cos30° + |
6 |
× cos120° |
||||||||
|
|
|
|
|||||||||
20
