Решение линейных дифференциальных уравнений с помощью преобразований Лапласа
Идея метода в том, что решение диф. уравнения из области функции действительного переменного f(t), переносится в область комплексного переменного.
Р = a +j*ω (область комплекс переменного)
где α- вещественная часть комплексного переменного;
j *ω— мнимая часть комплексного числа.
J означает корень из минус 1, где операции решения принимает более простой вид. Вместе диф. уравнение решается алгебраически.
Полученное операторное решение переводится обратно в область действительного переменного.
Формально символ дифференцирования d/ dt заменяется оператором р.
соответственно
+р2
и
т.д.
Символ интегрирования ƒdt заменяется 1/Р.
Функция времени f(t) соответственно преобразуется, называется оригиналом, а функция f(p), полученная в результате преобразования -изображение.
Символ р - называют оператором, форму записи уравнения -операторной.
Функция f(p) получается умножением f(t) на экспоненциальную
функцию е
F(p) = ƒf(t)*e-pt*αt
Пример: 1) Найти изображение функции времени f(t) = е –pt Напишем выражение преобразования функции Лапласа и проинтегрируем:
F(p) = ƒf(t) *e-pt *t = -l/(α+p) *e-(α+p)t = 1/(α+p)
2) оригинал функции имеет вид
Onput < О
Δлвых=
Anput > О
Изменение входной величины элемента или системы имеет
скачкообразный характер.
Для нахождения по оригинальной функции соответствующих изображений и по изображениям оригиналов существуют специальные таблицы преобразования Лапласа.
|
F(t) оригинал |
F(p) изображение |
|
{1} |
1/Р |
|
А{1} |
А/Р |
|
t |
1/p2 |
|
t2 |
2/р4 |
|
tn/n |
1/ Pm+1 |
|
е±2t |
1 /Р±а |
|
sinαt |
1/ /(P2 +a2) |
|
соsαt |
P/(P2+a2) |
|
t∙e-αt |
1/(py+α)y2y |
|
t* sinat |
α/(P + a)2+a2 |
|
t*cosat |
P+α/(P + a)2+a2 |
Динамическими звеньями являются: переходная функция, передаточные функции и частично передаточная функция или частные характеристики.
Переходной функцией Хвых(х) называют изменения выходной величины во времени, вызванное единичным скачкообразным изменением входной величины Хвх = 1.
Переходную функцию получают постановкой диф. уравнения или уравнения в операторной форме переходного процесса Хвх =1.
Для диф уравнения
T*dХХвы/dt+ТХХвы=КХвх
Предположим что Хвх = 1, то получим
dXXвы
Т + ТХХвы = К
dt
Но режим этого уравнения относительно Хвых, найдем по Лапласу его
изображение:
Тррхвы + ТХХвы = К
Хвых = К/Т((+1)переходная функция для диф. уравнения
Графически изображение переходных функций зависит от динамических свойств звена и характера внесенных воздействий, и имеет вид аналогичных переходным процессам только с уменьшением ординате в Хвх раз.
Передаточной функций w(p) звена или системы называют отношение изображения по Лапласу выходной величины к отношению изображения
входной величины при нулевых начальных условиях.
Передаточная функция из диф уравнения звена или системы записанной в операторной форме.
Так для диф уравнения
Т* dХХвы/dt+XХвх
Найдем изображение функции по Лапласу
Хвых(Тр +1) = КХвх
Разделим обе части на Хвх и решим относительно Vbx/Xbx:
Хвых/Хвх = К/Тp-1 =W(p)
Передаточная функция
Частотой характеристикой называют функцию частоты, описывающей изменение амплитуды и фазы гармонических колебаний выходной величины элемента. Частотные характеристики отличаются от функции входного воздействия только по амплитуде и фазе.
Частотные характеристики САР
Их понятие следует из преобразований Фурье, являющегося частным случаем преобразования Лапласа. Аналогично ему преобразование Фурье представляет собой функциональное преобразование
F(jw)=∫f(t)e-JWt,dt
о
Заметим, что частотная характеристика получается из изображения функции по Лапласу, в котором Р заменяют на jco. Например, изображение по Фурье функции
Если на выход звена подать сигнал Хвх = Авх * sin ωt, то по окончании переходного процесса в звене на его выходе установится тот же гармонич сигнал, но с амплитудой Авх = ΔХ2 и отставание его по фазе на угол ср.
Хвх=Авых* sin(wt+φ)
Хвх
Зависимость отклонения амплитуды гармонических колебаний на выходе системы или звена к амплитуде колебаний на его выходе от частоты называется амплитудно-частотной характеристикой (АЧХ).
A(w) = Авых / Авх
Зависимость разности фаз выходных входных гармоничных колебаний называется фазо-частотной характеристикой (ФЧХ).
φ(w) = φ вых - φ вх
Отношение выходного гармоничного сигнала звена или системы к входному гармоническому сигналу, выраженная в комплексной форме называется амплитудно-фазовой характеристикой (АФХ) или частотной передаточной функцией.
АФХ объединяет АЧХ и ФЧХ и является комплексной функцией частоты и как видное комплексное число м.б. представлено в 3-х формах записи:
1) в виде суммы вещественной и мнимой частей
W(jω) = Re(ω)+jJm(ω)
2) в тригонометрической форме
W (jω) = А(ω) * [cos(φ (ω) + jsin(φ(ω)]
3) в показательной форме
W(jω) = A*ω*ejф(ω) Т.к, согласно теореме Эйлера:
cos(ω) +jsin(φ(ω)) = ejф(ω) приведенных формулах А(ω) - модуль,φ(ω) - фаза
причем:
Пример
Построить АФХ системы, описываемой дифф. уравнениями:
Преобразуем с учетом того, что J2 = - 1
Избавимся от мнимости в знаменателе, умножив его на сопряженное
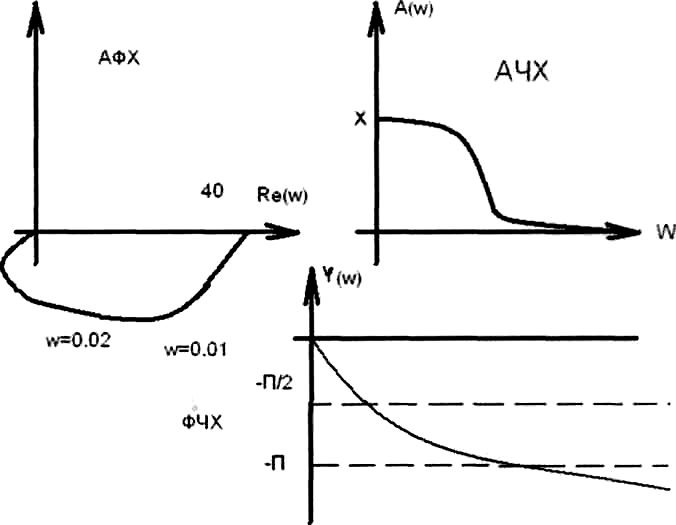
Подставляя в Re и Jm значения ω от 0 до °° , находим координаты точек на комплексной плоскости, кот являются концами векторов, проведенных из начало координат, соединяя эти концы векторов плавной
кривой, получили АФХ.
w 0 0.01 0.02 0.03
Re(w) 40 30 +16 +6
Im(w) 0 -19 -24 -20
0.04 0.05 0.06
+4 -1.1 -2.3
-16.7 -13.3 -10
График АФХ строится по известным АЧХ и ФЧХ:
lm(w)
*■*•
W
Различают 5 основных типов звеньев:
усилительные;
апериодические;
колебательные;
дифференцирующее;
интегрирующее.
Усилительное звено
Называется звено, у которого величина на выходе пропорцианальна величине на входе.
Уравнение усилительного звена
Хвых - К * Хвх
изменение входной величины изменение выходной величины
Передаточная функция усилит, звена
W(p) = К Wjw) = К; Re(w) = К; Im(w) = 0.
Устойчивое апериодическое звено 1 порядка
- такое звено, у кот при скачкообразном изменении величины на входе, величина на выходе апериодически стремится к новому установившемуся значению.
Диф. уравнение звена
Т*
dXXвы/dt+ ТХХвы=КХвх
Wp
= K/(Tp+l)
Примеры: пассивный электр. датчик t-ры; некоторые теплообменники, могут быть RC-фильтры и h-C фильтр.
Отличается от устойчивого только знаком " - " перед входной величины Т*dXХых/dt-Xвых = КХвх - диф. уравнение
W(p) = K/(Tp-l) - передаточная функция
Колебательное звено Устойчивое колебательное звено при скачкообразном изменении входной величины
Постоянная времени Т1 характеризует процесс затухания колебаний выходной величины, const T2 характеризует их раскачивание.
Если T1/T2≤2 то это колебательный процесс 1 -го порядка,
T1/T2≤2-
апериодический 2-го порядка.
Простейшим примером колебательного звена может служить колебательный контур, а также поплавковый и диф. манолитры.
Дифференцирующее звено
В котором величина на входе пропорциональна 1 -ой производной от величины на выходе, т.е. величина на входе пропорциональна скорости изменения величины на выходе и есть диф звено. Переходная функция диф. звена
W(p) = К*Р
АФХ W(jw)=jwt/(1 + jwT)
Alm(w)
Re(w)
w
Примером дифференциального звена является конденсатор и RC и LC фильтры.
Интегрирующее звено
- такое звено, в котором величина на входе пропорциональна интегралу по времени от величины на выходе, т.е. скорость изменения величины на выходе пропорциональна величине на входе. Диф уравнение интегрирующего звена:
Хввы = K/T*Xввхt
График итегрир. звена
Хвых = K*t
X
в
ы x
Передаточные функции итегр. звена
АЧХ
A(w) = K/W
-»-
Примером интегрир. звена является маломощные электродвигатели у которых угловая скорость строго пропорциональна напряжению, приложенному к якорю.
Звено запаздывания
Звено, у кот выходная величина точно воспроизводит входную, только с некоторым запаздыванием по времени
ФЧХ Хвых = Хвх(t-τ)
W(p) – e-pτ
jwτ
АФХ W(jw) = e –
Re(w)
АЧХ A(w) = 1
A