1.2.Сплайн 2-го порядка s(X).

На каждом из отрезков (x_i, x_i+1 ) функция у = f(x) приближается параболой

S(x) =

В узлах х = х_i ставятся следующие условия

1. 

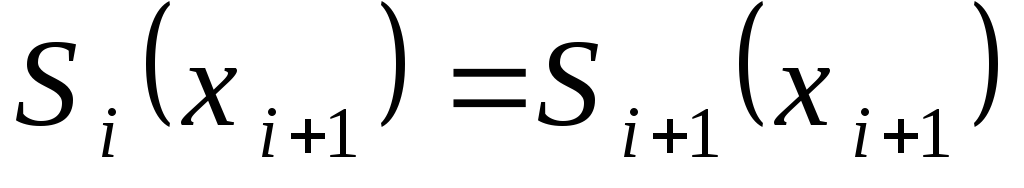2. - непрерывность функции S (x) в узлах

x_i , i = 1, 2, …, n-1.

3. - непрерывность первой производной функции

S (x) в узлах x_i , i = 1, 2, …, n-1.

Используя 1) - 3) определяем а_i, b_i, с_i.

1. Из условия следует, что

.

Сюда можно дописать дополнительный коэффициент .

2. Из условия 2) и 3) получаем систему

Из последней системы определяются

.

Подставляя в первую систему, получим

или

Окончательно

(1.4)

Для однозначной разрешимости системы (1.4) не хватает одного условия. Для этого дополнительно ставится условие .

Если неизвестно, то приближаем ее.

Тогда получится условие

. (1.5)

Теперь все коэффициенты с_i определяются по формуле

.

1.3. Расчетные формулы сплайна 2-го порядка.

1. Сначала вычисляются все коэффициенты .

2. Задается значение первой производной функций у=f (x) на левой границе отрезки [а,b], т.е. .

3. Из соотношения рекуррентно определяются все коэффициенты..

4. По формуле

определяются все с_i.

1.4. Переменные и структурная схема расчета.

Для составления программы вводятся следующие параметры расчета:

Массивы. - значения функций в целых узлах;значения функций в промежуточных узлах;коэффициенты сплайна 2-го порядка;значения сплайна в промежуточных точках;

отклонение;

средняя арифметическая погрешность вычисления;

средне-квадратическое отклонение погрешности вычисления. Константы a, b, n, h=(b-a)/n; k; переменные Ma, SІ, х.

С началотруктурная схема расчета.

а, в, n, k, f(x),b[0]

- - - - - - - - - - - ввод начальных данных

I: = Ø, n, 1

У[i] = f(x)

I : = Ø, n-1, 1

У1[i] = f(x)

I: = Ø, n-1, 1

b[i+1]: = 2(У[i+1]- У[i]) / h-b[i]

I : = Ø, n-1, 1

C[i] = (b[i+1]-b[i]) / h

I: = Ø, n-1, 1

Ma : = Ø

I : = Ø, n-1, 1

Ma : = Ma + D [i] / n

SI : = 0

SI : = SQRT (SI)

I

конец

: = Ø, n-1, 1

SI: = SI + (D[i] - Ma)²/(n-1)

Рис.2

Выводы:

На лекции 2 мы:

1. рассмотрели сплайн второго порядка,

2. получили расчетные формулы для вычисления коэффициентов сплайна второго порядка,

3. написали блок-схему программы вычисления функции в промежуточных точках при помощи сплайна второго порядка.

Лекция 3.

План лекции:

Схема расчета падения давления на контуре нефтяной залежи при упругом режиме (прямоугольная область).

Аппроксимация Карслоу-Егеря.

Расчет падения давления на контуре нефтяной залежи при упругом режиме (круговой контур).

Формула Дюамеля для расчета давления на контуре нефтяного месторождения.

Расчет падении давления в пласте при упругом режиме.

2.1. Постановка задачи.

Задача 1. Между двумя параллельными сбросами находится нефтяная залежь 2 (рис.2.1), за пределами которой расположена бесконечно простирающаяся водоносная область. Стрелками показан приток воды из законтурной области. Ширина залежиb=1000м, толщина пласта h=15м, проницаемость водоносной области к=0,2·10-12 м2, вязкость законтурной воды , коэффициент пьезопроводности пласта -

1 у 1' О х 2 в Рис.2.1

Отбор жидкости из залежи изменяется во времени следующим образом

где t_* – время ввода месторождения в разработку .

Требуется определить изменение давления на контуре нефтеносности (t)=P₀-P(t) ,т.е. при у=0 (см. рис.2.1) по сравнению с начальным пластовым давлением после начала разработки залежи.

2. Решение задачи 1.

Для расчета изменения во времени давления на контуре нефтяной залежи используя аппроксимацию Карслоу и Егеря [1] имеем:

(2.1)

Выводы :

На лекции 3 мы разобради:

1. Схемау расчета падения давления на контуре нефтяной залежи при упругом режиме (прямоугольная область).

2. Аппроксимацию Карслоу-Егеря.

3. Схему расчета падения давления на контуре нефтяной залежи при упругом режиме (круговой контур).