3. Постановка прямой задачи электроразведки для горизонтально-слоистой модели земли.

Теория электроразведки базируется на решении прямых и обратных задач электродинамики.

Прямой задачей называют отыскание элементов поля на поверхности или внутри заданной модели среды при известном расположении источников поля. Форму модели подбирают такой, чтобы она максимально соответствовала типичным геологическим моделям среды и в то же время допускала строгое математическое решение, на основе которого можно было бы производить количественные расчеты. Например, контакт двух сред, вертикальный или наклонный пласт, горизонтально-слоистое полупространство, шар, эллипсоид и другие.

Обратной задачей называют воссоздание внутренней структуры модели среды по найденному распределению элементов поля на ее поверхности или внутри среды. Например, по наблюденной аномалии потенциала естественного электрического поля определяют местоположение, форму и глубину залегания рудного тела, являющегося природным источником наблюдаемой аномалии; по результатам ВЭЗ делают заключение о последовательности залегания пластов с различной электропроводностью и находят глубину залегания границ пластов.

Таким образом, прямые и обратные задачи в совокупности составляют физико-математическое обеспечение приемов интерпретации.

Найдем потенциал электрического поля при следующих условиях:

1. среда состоит из конечного числа слоев, разделенных плоскими горизонтальными границами; в основании лежит слой, который простирается на бесконечную глубину, остальные слои имеют конечную мощность;

2. каждый слой электрически однороден и изотропен;

3. поле возбуждается точечным источником тока, который расположен на земной поверхности;

4. ток является постоянным или низкочастотным переменным;

При этом должны быть соблюдены следующие граничные условия:

1. на всех границах в земле электрический потенциал должен быть непрерывен;

2. на всех границах в земле вертикальная компонента плотности тока должна быть непрерывна;

3) на земной поверхности вертикальная компонента плотности тока должна быть равна нулю, за исключением бесконечно малой окрестности источника тока; причина этого состоит в том, что плотность тока в воздухе равна нулю и по условию (2) вертикальная компонента плотности тока в земле на нулевой глубине также должна быть равна нулю.

4) вблизи источника тока потенциал должен приближаться к бесконечности, как а на бесконечной глубине потенциал должен стремиться к нулю.

Электрический потенциал U в условиях постоянного тока удовлетворяет дифференциальному уравнению Лапласа U =0.

В данном случае, потенциал должен быть цилиндрически симметричен по отношению к вертикальной линии, проходящей через источник тока, поэтому удобнее перейти к цилиндрическим координатам z, r, (рис.4):

Рис.4.

.

Если мы хотим, чтобы решение этого уравнения было симметрическим по отношению вертикальной оси, то . Тогда уравнение упрощается:

(2.1)

Общее решение уравнение (2.1) можно представить в виде

, (2.2)

где - функция Бесселя нулевого порядка, - произвольные функции от.

В случае расположения точечного источника на поверхности горизонтально-слоистой земли, для каждого i-слоя можно написать

(2.3).

С учетом граничных условий (1)-(4) потенциал на земной поверхности имеет вид

, (2.4)

где I – сила тока, - удельное сопротивление 1-слоя,-переменная интегрирования,r - расстояния от источника тока до точки измерения,

- керн-функция Стефанеску, зависит от удельных сопротивлений - и глубин замечанияграницыi– слоя.

Если ввести керн-функцию Слихтера

(2.5)

то уравнение (2.4) можно записать в более компактном виде:

(2.6)

Для керн-функций Слихтера можно ввести более удобные рекурентные соотношения Пекериса. На рис.5 слева изображена

Рис.5.

первоначальная совокупность слоев, а справа показано, как действуют рекурентные соотношения Пекериса: новый слой добавляется сверху, а электроды переносятся на верхнюю поверхность нового слоя. Тогда на верхнем слое можно определить из соотношений:

(2.7)

- для основания, где - мощностьi-слоя. Уравнения (2.7) может быть обращено, т.е.

(2.8).

В такой форме рекурентное соотношение Пекериса описывает удаление верхнего слоя, сопровождаемое переносом электродов на поверхность подстилающего слоя, т.е. рекурцией к нижней границе.

Согласно О.Куфуду введем трансформанту сопротивления.

(2.9)

Выразив рекурентные соотношения Пекериса через трансформанту сопротивления, получим

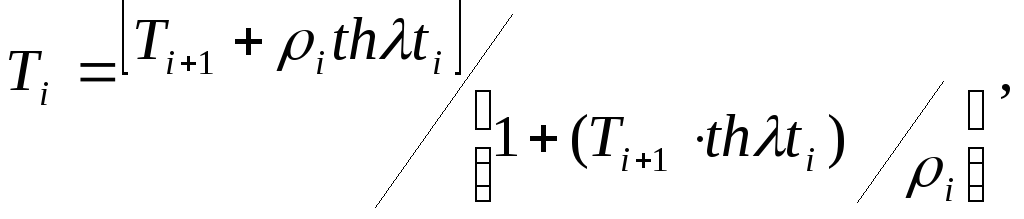(2.10)

и в обращенной форме

(2.11)

Трансформанта сопротивления имеет физическую размерность удельного сопротивления. Эта функция параметров слоев и параметра , который имеет размерность обратного расстояния. Теперь можно определить соотношение между кажущимся сопротивлениями трансформантой сопротивления для установки Шлюмберже. Для этого в формулу

где - полуразносы питающих и измерительных электродов (рис.6), надо вместо подставить выражение из (2.4).

Тогда получим Рис.6.

(2.12)

где

Это уравнения согласно (2.5), (2.8) удобно записать в виде

(2.13)

По последнему уравнению можно теоретически определять , т.е. решать прямую задачу ВЭЗ.

Выводы:

На лекции 19 были рассмотрены:

1. Постановка прямой задачи электроразведки для горизонтально-слоистой модели земли.

2. Решение уравнения Лапласа.

3. Трансформанта сопротивления.

4. Соотношения Пекериса

Лекция 20.

План лекции:

Численное решение прямой задачи электроразведки с помощью линейных фильтров.

Алгоритм и блок-схема решения прямой задачи.

Переменные и константы для составления программы на языке Турбо-Паскаль.