1.9. Сили в механiцi

1.9.1. Сили пружності

• Закон Гука:

F = – kx,

де k – коефіцієнт жорсткості, х – величина пружної деформації.

• Напруження при пружній деформації

,

де S– площа поперечного перерізу зразка, l –його довжина,Δl–абсолютна зміна довжини тіла,Е–модуль Юнга.

• Напруження при деформації стиску

,

де – коефіцієнт стисливості, –відносне потовщення стержня при стисненні;

• Зміна поперечних розмірівстрижня при деформаціях поздовжнього розтягу чи стиснення характеризують числом Пуассона:

μ = βּЕ.

• Кут зсуву при деформаціях зсуву:

,

де τ– дотичне напруження,G – модуль зсуву (модуль Кулона).

1. Задачi

306. Верхнiй кiнець свинцевого дроту дiаметром 10 см та довжиною 1 м закрiпили жорстко, а до нижнього кiнця пiдвiсили вантаж масою 50 кг. Знайти напруження матерiалу: 1) бiля нижнього кiнця дроту; 2) на серединi довжини; 3) бiля верхнього кiнця дроту. [0,6∙10⁶ Н/м²; 0,9∙10⁶ Н/м²; 1,2∙10⁶ Н/м²].

307. Вантаж масою 10 кг, прив’язаний до дроту та обертається з частотю 2,2 с^-1 навколо вертикальної осi, яка проходить через дрiт, а вантаж при цьому ковзає горизонтальною поверхнею без тертя. Довжина дроту 2 м, площа поперечного перерiзу 28 мм². Знайти напруженя металу дроту, знехтувавши його масою. [136 МН/м²].

308. До сталевого стрижня довжиною 3 м та дiаметром 10 см пiдвiсили вантаж масою 2,5∙10³ кг. Визначити напруження металу у точці підвісу стрижня, вiдносне та абсолютне видовження стрижня. [10⁶ Н/м²; 5∙10^–6; 1,5∙10^–5 м].

309. Дрiт довжиною 10 м та дiаметром 1 мм натягнуто практично горизонтально. Коли до середини дроту прив’язали вантаж масою 2 кг, то дрiт розтягнувся так, що точка пiдвiсу опустилась на 9 см. Визначити модуль Юнга матерiалу дроту. [1,95∙10¹¹ Па].

310. З допомогою динамометра, жорсткiсть пружини якого 29,4 Н/м, рiвномiрно перемiстили брусок масою 1 кг на вiдстань 10 см. Порiвняти роботу на подолання сили тертя (А₁) з роботою на розтягування пружини до початку руху бруска (А₂), якщо коефiцiєнт тертя бруска по поверхнi 0,3. [А₁/А₂=200].

311. Двi пружини жорсткiстю 200 Н/м та 400 Н/м з’єднанi послiдовно. Визначити абсолютну деформацiю першої пружини, якщо друга внаслiдок прикладання сили деформувалась на 2 см. [4 см].

312. Визначити жорсткiсть системи двох пружин при їхньому послiдовному та паралельному з’єднаннi, якщо жорсткостi пружин 400 та 100 Н/м. [80 Н/м; 500 Н/м].

313. Двi пружини з коефiцiєнтами жорсткостi 300 та 100 Н/м з’єднано послiдовно та розтягнуто деякою постiйною силою. Знайти вiдношення потенцiальних енергiй пружин. [1/9].

314. Пружину спочатку розтягли силою 50 Н, а потiм до неї приклали додаткову силу 80 Н, внаслiдок чого вона розтяглась ще на 20 см. Яка сумарна робота була виконана? [21 Дж].

315. З якою швидкiстю вилетить iз пружинного пiстолета куля масою 10 г, якщо вона була стиснута на 5 см, а жорсткiсть пружини дорiвнює 200 Н/м? [7 м/с].

316. Вагон масою 10 т, рухаючись зi швидкiстю 1 м/с, налiтає на пружинний буфер і зупиняється. Яка жорсткiсть пружини буфера, якщо вона здеформувалась на 50 см? [40 кН/м].

317. Дві пружини з жорсткостями 300 та 500 Н/м з’єднано послідовно та розтягнуто так, що абсолютна деформація другої пружини дорівнює 3 см. Знайдіть роботу розтягу пружин. [0,6 Дж].

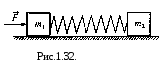318. На горизонтальному столі лежать два бруски масами т₁=1 кг та т₂=2 кг, з’єднаних нерозтягнутою пружиною (рис.1.32). Яку найменшу горизонтальну силу треба прикласти до першого бруска, щоб другий брусок почав рухатись? Коефіцієнт тертя брусків об поверхню однаковий і дорівнює 0,2. [4 Н].

319. Металевий диск стискує вертикально встановлену пружину на 2 мм. На скільки стиснеться дана пружина, якщо цей диск впаде на пружину з висоти 5 см? [16 мм].

320. Двi пластинки масами 200 г та 300 г з’єднанi пружинкою та розташованi так, що пластинка меншої маси розміщена над пластинкою більшої маси, яка лежить на столi (рис. 1.33). З якою силою необхiдно натиснути на верхню пластинку, щоб пiсля припинення дiї сили верхня пластинка, пiдскочивши, припiдняла й нижню. Масу пружин не враховувати. [4,9 Н].