Важным направлением в анализе совокупности является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.

1. Условия применения рядов с равными интервалами

До этого мы изучали только правила построения интервальных рядов с равными интервалами. В то же время, очень часто при анализе реальных данных приходится строить вариационные ряды с неравными интервалами. Количество групп определяется в каждом случае индивидуально, в зависимости от изучаемой совокупности.

Для оценки качества группировки данных (качества разбиения на интервалы) могут быть использованы эмпирическое корреляционное отношение и график плотности распределения единиц признака (полигон распределения частот и гистограмма).

Первоначально строят интервальный ряд с равными интервалами и анализируют возможность его применения. Применение равных интервалов возможно, если вариация признака (разница между максимальным и минимальным значением) не очень сильная и распределение является равномерным (все группы достаточно наполнены, линия полигона частот не имеет резких перепадов и зигзагов).

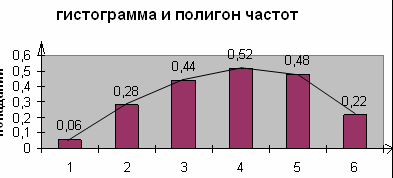
Если же эти условия не соблюдаются, то тогда нужно строить интервальные ряды с неравными интервалами. Неравные интервалы делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные, равночастотные и специализированные.

Приблизительно число интервалов m можно оценить исходя только из объема выборки n по формуле Стерджесса или по таблице:

Объем выборки, n	25-40	40-60	60-100	100-200	Больше 200
Число интервалов, k	5-6	6-8	7-10	8-12	10-15

2. Интервальный ряд с равночастотными интервалами

Интервальный ряд с равночастотными интервалами: частота каждого интервала одинакова.

Когда вариация признака очень сильна, вместо рядов с равными интервалами лучше использовать равночастотные интервалы (ряд, в котором все интервалы имеют одинаковую частоту).

Число групп в равночастотных интервалах обычно принимают равным 4 (квартильное распределение), 5 (квинтильное распределение), 10 (децильное распределение). Таким образом, в каждой группе содержится 25%, 20%, 10% единиц совокупности соответственно.

3. Интервальный ряд с произвольными интервалами

Интервальный ряд с произвольными интервалами: границы интервала задаются степенью однородности данных внутри интервала (т.е. коэффициентом вариации).

Всю изучаемую совокупность выстраивают в порядке возрастания или убывания варьирующего признака, а затем берут первые значения ряда до тех пор, пока коэффициент вариации не будет равен 33%. Это будет свидетельствовать об образовании первой группы, которая исключается из исходной совокупности.

Оставшаяся часть принимается за новую совокупность, для которой повторяется алгоритм образования первой группы. И так до тех пор, пока все единицы совокупности не будут объединены в группы.

4. Специализированные интервалы

В типологических группировках используются специализированные интервалы. Границы в них устанавливаются там, где начинается переход от одного качества к другому. Наметить точки перехода можно только на основе теоретического анализа, используя для выделения типов совокупность признаков, характеризующих различные стороны изучаемого явления.