
Статистическое распределение и его основные характеристики
Показатели, характеризующие вариацию значений признака
Для анализа вариационных рядов используются три группы показателей:
- показатели центра распределения;
- показатели степени вариации;
- показатели формы распределения.
Показатели центра распределения
Для характеристики центра распределения в вариационном ряду применяются : среднее значение признака, медиана, мода.
Показатели степени вариации признака
Часто при описании статистических данных приходится оперировать понятием «однородность». Значимость однородности в статистическом анализе трудно переоценить, так как она напрямую влияет на точность рассчитываемых показателей и качество аналитических выводов. Чем однороднее данные, тем надежнее и адекватнее реалиям результаты статистического анализа.
Однородность – понятие относительное и растяжимое. Она не имеет точных границ и критериев. Под однородными данными следует понимать некоторый уровень их рассеяния, при котором рассчитываемые статистические показатели (средняя и проч.) будут давать надежную и качественную характеристику анализируемой совокупности.
Основным мерилом разброса (и однородности) данных являются показатели вариации: дисперсия σ2, среднеквадратическое отклонение σ, среднее линейное отклонение a. Однако все они не дают характеристики степени разброса данных. Для преодоления этой проблемы был придуман так называемый коэффициент вариации, который рассчитывается как соотношение стандартного отклонения и средней величины.

В статистике принято считать, что, если значение коэффициента менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной..
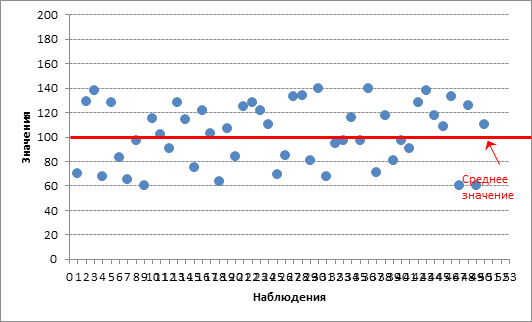
Для указанных данных коэффициент вариации составил 24%, то есть совокупность вроде как однородная получилась (менее 33%).
Теперь увеличим диапазон разброса до плюс/минус 80.
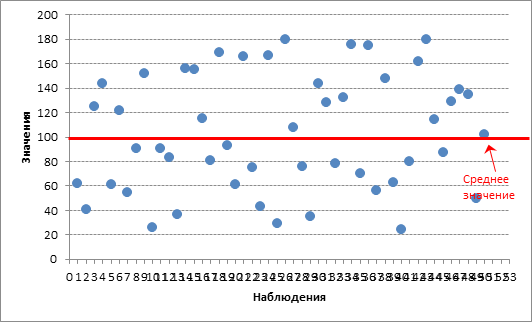
Чисто визуально отчетливо видно, что данные стали более рассеяны. Коэффициент вариации на этот раз составил 45%, следовательно, совокупность стала неоднородной.
Чем более однородны данные, тем ближе они находятся к среднему значению. Чем менее однородны, тем больше рассеяны и находятся дальше друг от друга и от своей средней.
Теперь посмотрим, как измеряется вариация, с помощью каких показателей и что они обозначают.
Размах вариации
Первый показатель мы уже упомянули – это размах вариации, то есть разница между максимальным и минимальным значением. Думаю, здесь пояснять нечего, все элементарно. Для порядка напишем формулу:
![]()
С одной стороны показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла.
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
Данный показатель не дает устойчивую оценку, так как все зависит от двух, как правило, случайных значений – от максимума и минимума. Таким образом, размах вариации очень неустойчивая величина.
