Примеры решения задач

Задача 1. Определить токи в ветвях данной цепи (рис. 11.4.).

Решение

Рассчитаем электрическую цепь с помощью правил Кирхгофа.

1. Определим количество узлов и ветвей в цепи (2 узла, 3 ветви).

2. Произвольно расставим токи в ветвях.

3. По первому закону Кирхгофа составим уравнение, где – число узлов.

Составим уравнение для узла А:

Токи и входят в узел, их берем со знаком плюс.

4. Произвольно выбираем направление обхода контуров (по часовой стрелке).

5. Число независимых уравнений, составляемых по второму правилу Кирхгофа, должно быть меньше числа замкнутых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбирать произвольно. Все следующие контуры следует выбирать так, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Для контура 1–2–А–В–1

.

Токи I₁ и I₂ совпадают с направлением обхода, поэтому произведения иберутся со знаком “плюс”. Направление действиясовпадает с направлением обхода, берется знак “плюс”. Направление действияпротивоположно обходу, поэтому знак “минус”.

Для контура 1–2–3–4–1

После подстановки известных числовых значений получим систему уравнений:

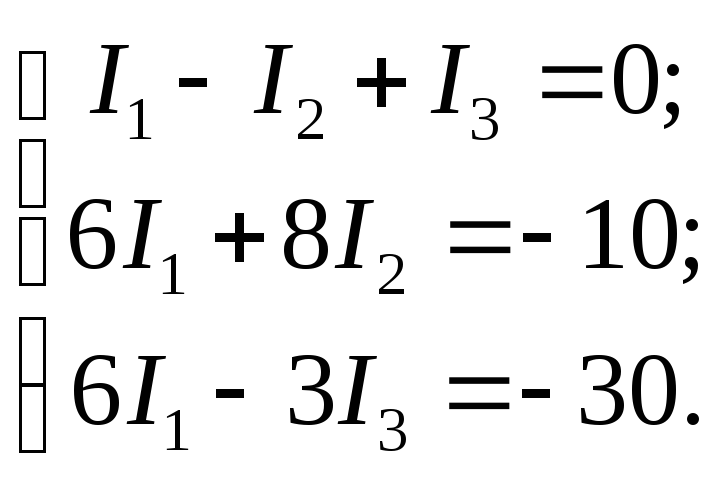
Решим систему уравнений методом определителей:

; ;.

Составим и вычислим определитель системы :

.

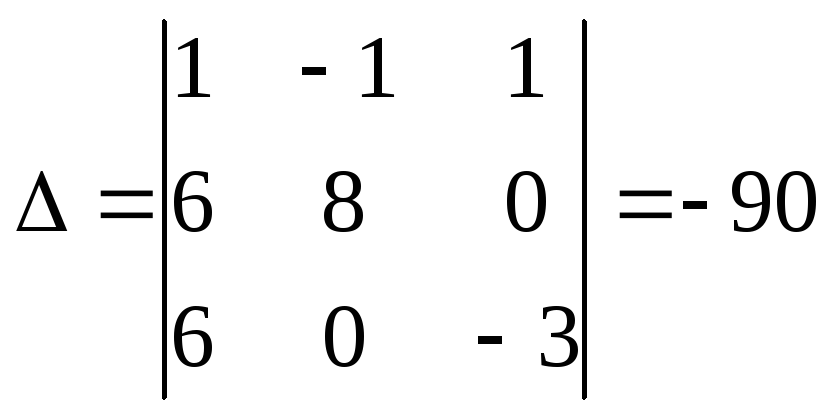Составим и вычислим определители ₁, ₂:

; А;А.

; А.

Ток в первой ветви течет в направлении, противоположном произвольно выбранному. Е₃ работает как генератор, а Е₁ и Е₂ являются потребителями.

Ответ: А;А;А.

Задача 2: Определить в данной схеме (рис. 11.5).

Решение

В данной цепи три узла (а, с, в) и две ветви (ас и св). Запишем закон Ома для каждой ветви:

ас: ;

св: .

Полученную систему уравнений решаем любым алгебраическим методом и находим

Ответ: В.

Задача 2-а (резерв). Найти показание амперметра (рис. 11.6).

Ответ: А.

Задача 3. Определить ток в цепи и потенциалы точек 2, 3, 4 относительно точки 1, потенциал которой принять равным нулю. Построить потенциальную диаграмму (рис. 11.7).

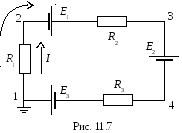
Решение

1. Выберем произвольно направление тока и обхода (лучше одинаковое) по часовой стрелке.

2. Запишем закон Ома для замкнутой цепи, учтя знаки ЭДС:

.

3. Запишем закон Ома для участков цепи и, решая уравнения, вычислим потенциалы точек 2, 3, 4:

1 – 2: В.

2 – 3: В.

3 – 4: В.

Для построения потенциальной диаграммы выбираем оси координат, на которых в масштабе откладываем сопротивление R и потенциалы :

По потенциальной диаграмме найдем В (рис. 11.8).

Ответ: А;В;В;В.

Задача 4. Как изменятся показания приборов, если лампочка Л₃ перегорит? Сопротивления лампочек одинаковы (рис. 11.9). Исследование режима работы цепи лучше оформить в виде таблицы. Перед решением выяснить, как включены лампочки, почему будут изменяться показания приборов. Необходимо считать E = const, r = const.

Таблица 11.1

№	Было	Стало	Вывод
1
2
3
4
5

Ответ: Внешнее сопротивление увеличивается, ток в цепи уменьшается (показание амперметра уменьшается), напряжение на всей внешней цепи, измеряемое вольтметром V, увеличивается; на участках U₁ уменьшается, U₂ увеличивается.

Задача 5. Проволочный куб составлен из проводников. Сопротивление каждого проводника, составляющего ребро куба, R₁ = 1 Ом. Вычислить сопротивление этого куба, если он включен в электрическую цепь, как показано на рис. 11.10, а, б.

Решение

а) Найдем на кубе точки равных потенциалов и соединим их в узлы. Эквивалентная схема изображена на рис. 11.11.

Общее сопротивление .

Ответ: Ом.

б) Относительно точек А и В куб имеет плоскость симметрии. Точки, лежащие на плоскости симметрии, соединяем в узел. Эквивалентная схема изображена на рис. 11.12.

;

;

.

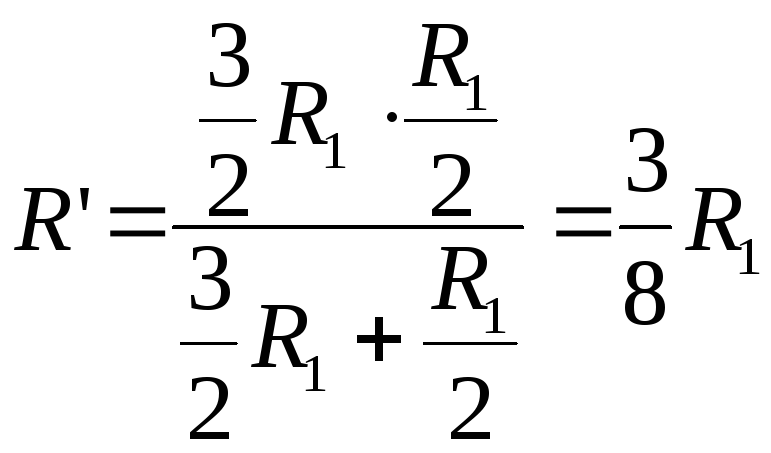Ответ: Ом.

Задачи для самостоятельного решения

Задача 1. Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента E = 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Найти силу тока во внешней цепи.

Ответ: I = 2 А.

Задача 2^*. В цепь, составленную из источника ЭДС с внутренним сопротивлением r = 1 Ом и сопротивления R = 100 Ом, включается вольтметр, первый раз – параллельно сопротивлению, второй – последовательно с ним. Показания вольтметра оказались одинаковыми. Найти сопротивление вольтметра.

Ответ: Ом.

Задача 3^*. Сила тока в проводнике равномерно нарастает от I₀= 0 до I = 3 А за 10 с. Определить заряд, прошедший в проводнике.

Ответ: q = 15 Кл.

Задача 4. Определить плотность тока в железном проводнике длиной м, если провод находится под напряжениемU = 6 В, (Омм).

Ответ: А/м².

Задача 5. Напряжение на шинах электростанции U = 6600 В. Потребитель находится на расстоянии l = 10 км. Какого сечения нужно взять медный провод для устройства двухпроводной линии электропередачи, если сила тока в линии I = 20 А и потери напряжения в проводах не превышают 3 %?

Ответ: S = 3,410^-5 м².

Задача 6. Катушка и амперметр соединены последовательно и присоединены к источнику тока. К зажимам катушки присоединен вольтметр сопротивлением Ом. Показания амперметраI = 0,5 А, вольтметра U = 100 В. 1) Определить сопротивление катушки. 2) Сколько процентов от точного значения сопротивления катушки составит ошибка, если не учитывать сопротивления вольтметра?

Ответ: 1) R = 250 Ом; 2) 20 %

Задача 7. Две батареи (E₁ = 10 В, r₁ = 1 Ом, E₂ = 8 В, r₂ = 2 Ом) и резистор сопротивлением R = 6 Ом соединены, как показано на рис. 11.13. Найти силу тока в батареях и резисторе.

Ответ: I = 6,4 A; 5,8 A; 0,6 A.

Задача 8. К элементу с Е = 1,5 В присоединили катушку с сопротивлением R = 0,1 Ом. Амперметр показал силу тока I₁ = 0,5 A. Когда к элементу присоединили последовательно еще один элемент с такой же ЭДС, то сила тока в той же катушке стала I₂ = 0,4 A. Определить внутреннее сопротивление первого и второго элементов.

Ответ: r₁ = 2,9 Ом; r₂ = 4,5 Ом.

Задача 9. Проволока имеет сопротивление 36 Ом. Когда ее разрезали на несколько равных частей и соединили эти части параллельно, то получилось сопротивление 1 Ом. На сколько частей разрезали проволоку?

Ответ: n = 6.

Задача 10. К источнику с ЭДС E = 18 В и внутренним сопротивлением Ом подключены три одинаковых проводника сопротивлениемОм каждый, соединенных по схеме, изображенной на рис. 11.14. Сопротивлением соединительных проводов АС и ВД можно пренебречь. Определить силу тока, текущего через каждое сопротивление.

Ответ: I = 3 A.

Задача 11. Два элемента (E₁ = 1,2 В, r₁ = 0,1 Ом, E₂ = 0,9 В, r₂ = 0,3 Ом) соединены одноименными полюсами. Сопротивление соединительных проводов R = 0,2 Ом. Определить силу тока в цепи.

Ответ: I = 0,5 А.

Задача 12. Два источника тока (E₁ = 8 В, r₁ = 2 Ом, E₂ = 6 В, r₂ = 1,5 Ом) и резистор R = 10 Ом соединены, как показано на рис. 11.15. Вычислить силу тока, текущего через резистор.

Ответ: I = 0,63 A.

Задача 13. Определить силу тока в сопротивлении R₃ и напряжение на концах этого сопротивления, если E₁ = 4 В, E₂ = 3 В, R₁ = 2 Ом, R₂ = 6 Ом, R₃ = 1 Ом. Внутренним сопротивлением источников тока пренебречь (рис. 11.16).

Ответ: I₃ = 0, U₃ = 0.

Задача 14. Три батареи с ЭДС E₁ = 12 В, E₂ = 5 В, E₃ = 10 В и одинаковыми внутренними сопротивлениями, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединительных проводов ничтожно мало. Найти силу тока, текущего через батареи.

Ответ: I = 3 A; 4 A; 1 A.

Задача 15. Три источника тока (E₁ = 11 В, E₂ = 4 В, E₃ = 6 В) и три резистора (R₁ = 5 Ом, R₂ = 10 Ом, R₃ = 2 Ом) соединены так, как показано на рис. 11.17. Определить силу тока в резисторах. Внутреннее сопротивление источников пренебрежимо мало.

Ответ: I = 0,8 A; 0,3 A; 0,5 A.

Задача 16. Три сопротивления R₁ = 5 Ом, R₂ = 1 Ом, R₃ = 3 Ом и источник тока E₁ = 1,4 В соединены, как показано на рис. 11.18. Определить ЭДС источника тока, который нужно включить в цепь между точками А и В, чтобы в сопротивлении R₃ шел ток силой I = 1 A в направлении, указанном стрелкой. Сопротивлением источников тока пренебречь.

Ответ: E = 3,6 В.

Задача 17. Сколько витков нихромовой ( = 110^–6 Омм) проволоки диаметром 1 мм надо навить на фарфоровый цилиндр радиусом 2,5 см, чтобы получить печь сопротивлением 40 Ом? Какой ток пойдет по проволоке при включении печи в сеть с напряжением 220 В?

Ответ: N = 200 витков; I = 5,5 A.

Задача 18. Сетка состоит из одинаковых звеньев. Сопротивление каждого звена R = 1 Ом. Найти сопротивление между точками А и В (рис. 11.19).

Ответ: R_АВ = 1,5 Ом.

Задача 19^*. Зайти сопротивление между точками А и В цепи при разомкнутом и замкнутом ключе. Сопротивление каждой стороны и диагонали квадрата R = 1 Ом (рис. 11.20).

Ответ: При разомкнутом ключе R_АВ = = 0,625 Ом; при замкнутом ключеR_АВ = = 0,5 Ом.

Задача 20^*. Найти сопротивление между соседними вершинами проволочного куба. Сопротивление каждого из ребер куба R₁ = 1 Ом.

Ответ: Ом.

Задача 21. Найти сопротивление между вершинами куба, расположенными на диагонали одной из его граней. Сопротивление каждого из ребер куба R₁ = 1 Ом.

Ответ: Ом.

Задача 22^*. Провод АСВ изогнут так, что точки А, С и В находятся на вершинах правильного треугольника. К серединам сторон АС и ВС подключена перемычка EF из провода с вдвое меньшей площадью сечения. К точкам А и В подано напряжение U = 3 В. Найти падение напряжения на перемычке (рис. 11.21).

Ответ:В.

Задача 23. Катушка из медной проволоки ( = 1,710^–8 Омм) имеет сопротивление R = 10,8 Ом. Масса проволоки 3,42 кг. Сколько метров проволоки и какого диаметра намотано на катушке?

Ответ: l = 500 м; d = 1 мм.

Задача 24. Элемент, амперметр и сопротивление включены последовательно. Сопротивление сделано из медной проволоки (Омм) длиной 100 м и поперечным сечением 2 мм², сопротивление амперметра 0,05 Ом, амперметр показывает 1,43 А. Если же взять сопротивление из алюминиевой проволоки (Омм) и длиной 57,3 м и поперечным сечением 1 мм², то амперметр покажет 1 А. Найти ЭДС элемента и его внутреннее сопротивление.

Ответ: E = 2 В; r = 0,5 м.

Задача 25. В схеме ЭДС батареи E = 100 В, R₁ = 100 Ом, R₂ = 200 Ом, R₃ = 300 Ом. Какое напряжение покажет вольтметр, если его сопротивление 2000 Ом? Сопротивлением батареи и проводов пренебречь (рис. 11.22).

Ответ: U = 80 В.

Задача 26. ЭДС элемента E =1,6 В и внутреннее сопротивление r = 0,5 Ом. Чему равен КПД элемента при силе тока в 2,4 А?

Ответ: КПД = 25 %.

Задача 27. Найти ЭДС батареи (по схеме предыдущей задачи), если R₁ = R₂ = R₃ = 200 Ом. Вольтметр показывает 100 В, его сопротивление 1000 Ом. Сопротивлением батареи и проводов пренебречь (рис. 11.22).

Задача 28. Найти показания амперметра и вольтметра в схемах а, б, в (рис. 11.23). Сопротивление вольтметра 1000 Ом, R₁ = 400 Ом, R₂ = 600 Ом, ЭДС батареи E = 110 В. Сопротивлением батареи и амперметра пренебречь.

Ответ: а) I = 0,57 А, U = 110 В;

б) I = 0,09 А, U = 53,2 В;

в) I = 0,142 А, U = 53,2 В.

Задача 29. Два элемента (E₁ = E₂ = 2 В; r₁ = 1 Ом r₂ = 2 Ом) соединены по схеме (рис. 11.24). Сила тока, текущего через первый источник, равна I₁ = 1 А. Найти остальные токи и внешнее сопротивление R.

Ответ: I₂ = 0,5А; I₃ = 1,5 А; R = Ом.

Задача 30. Решить предыдущую задачу, если E₁ = E₂ = 4 В, r₁ = r₂ = 0,5 Ом, I₁ = 2 А (рис. 11.24).

Ответ: I₂ = 2 А; I₃ = 4 А; R = 0,75 Ом.

Задача 31. Какую силу тока показывает миллиамперметр в схеме, если E₁ = 2 В, E₂ = 1 В, R₁ = 1000 Ом, R₂ = 500 Ом, R₃ = 200 Ом, сопротивление миллиамперметра R_А = 200 Ом (рис. 11.25).

Ответ: I = 0,45 мА.

Задача 32. Решить предыдущую задачу, если E₁ = 1 В, E₂ = 2 В, R₃ = 1500 Ом, R_А = 500 Ом и падение напряжения на сопротивлении R₂ U₂ = 1 В (рис. 11.25).

Ответ: I = 1 мА.

Задача 33. Два элемента с одинаковой ЭДС в 2 В и одинаковым внутренним сопротивлением, равным 0,5 Ом, соединены с сопротивлениями R₁ = 0,5 Ом, R₂ = 1,5 Ом, как показано на рис. 11.16. Найти токи в ветвях.

Ответ: I = 2,22 А; 0,44 А; 1,78 А.

Задача 34. Определите общее сопротивление между точками А и В, если R₁ = 1 Ом, R₂ = 3 Ом, R₃ = R₄ = R₆ = 2 Ом, R₅ = 4 Ом.

Ответ: R = 1,2 Ом.

Задача 35. Амперметр показывает силу тока I = 1,5 A. Сила тока через сопротивление R₁ равна I₁ = 0,5 A. Сопротивление R₂ = 2 Ом, R₃ = 6 Ом. Определите сопротивление R₁, а также силу токов I₂, I₃, протекающих через сопротивления R₂ и R₃. Сопротивления включены параллельно.

Ответ: R₁ = 3 Ом, I₂ = 0,75 A, I₃ = 0,25 A.

Задача 36. По алюминиевому проводу сечением 0,2 мм² течет ток 0,2 А. Определите силу действующую на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление алюминия 26 нОмм.

Ответ: F = 4,1610^-21 Н.

Задача 37. Определите ток короткого замыкания источника ЭДС, если при внешнем сопротивлении R₁= 50 Ом ток в цепи I₁= 0,2 А, а при R₂= 110 Oм - I₂=0,1 А.

Ответ: I_кз = 1,2 А.

Задача 38. Два источника ЭДС 2 В и 1,5 В и внутренними сопротивления-ми 0,5 Ом и 0,4 Ом соответственно включены параллельно сопротивлению R = 2 Ом. Определите силу тока через это сопротивление.

Ответ: I = 0,775 А.

Задача 39. Даны Е₁=Е₂ =Е₃, R₁= 48 Oм, R₂ = 24 Oм, падение напряжения U₂ на сопротивлении R₂ равно 12 В. Пренебрегая внутренним сопротивлением элементов, определите: 1) силу тока во всех участках цепи; 2) сопротивле-ние R₃.

Ответ: 1) I₁ = 0,25 A, I₂ = 0,5 A, I₃ = 0,75 A; 2) R₃ = 16 Ом .