3.Принцип оптимальності. Рівняння Беллмана

Принцип оптимальності

У техніці існує великий клас об'єктів і процесів, керування якими здійснюється на основі обмеженого числа рішень, прийнятих послідовно в деякі фіксовані моменти часу.

Визначення закону керування для таких процесів пов'язане з рішенням так званої задачі багатокрокового вибору. Керування дискретними системами може бути прикладом таких багатокрокових процесів.

Кожний безперервний процес можна представити як багатокроковий, якщо розглядати його в дискретні моменти часу. Підхід, що дозволяє знайти оптимальне рішення на основі багатокрокових процесів ухвалення рішення, одержав назву динамічного програмування.

В основі методу динамічного програмування лежить принцип оптимальності, сформульований Беллманом Р.

Оптимальна стратегія визначається лише станом системи в даний момент і не залежить від того, як система прийшла в дану точку (рис.3.1).

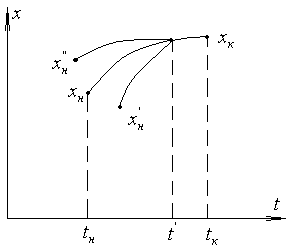
Рис. 3.1.

Під стратегією ми розуміємо правило прийняття рішень.

Принцип оптимальності може бути сформульований і по-іншому.

Якщо траєкторія системи оптимальна на відрізку часу , то кінцева ділянка цієї траєкторії на відрізкуу свою чергу є оптимальною траєкторією, де довільний момент часу (рис.3.10).

Із принципу оптимальності можна одержати необхідні умови оптимальності для безперервних і дискретних систем.

Безперервні системи. Рівняння Беллмана

Об'єкт описується рівнянням

Визначити керування і траєкторію, що доставляють екстремум функціоналу

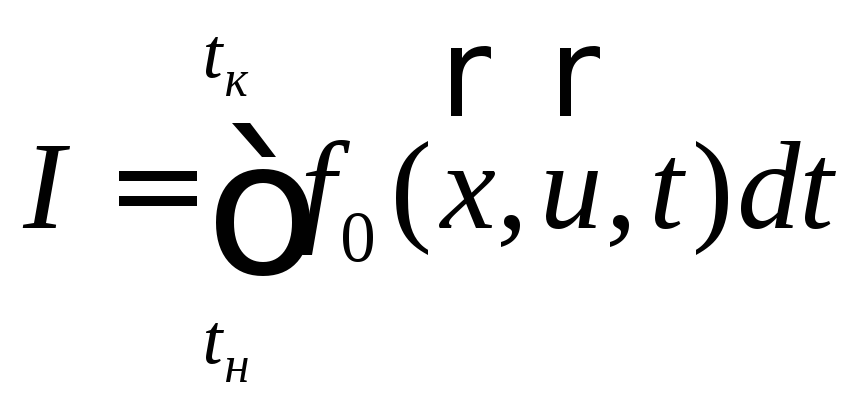
де фіксовано,

відкрита область.

Нехай відома оптимальна траєкторія , рис3.2. Розглянемо ділянку.

Відповідно до принципу оптимальності функціонал (3.2) досягає на ньому мінімум.

Введемо позначення

Рис. 3.2.

При певному керуванні мінімальне значення функціонала залежить тільки від і.

Функція називається функцією Беллмана.

Розглянемо дві близькі точки оптимальної траєкторії й.

Точка перебуває ближче до кінцевого стану. Тому, дотримуючись принципу оптимальності, ділянка траєкторії віддовже оптимальна.

Відповідно до теореми про середнє можна записати

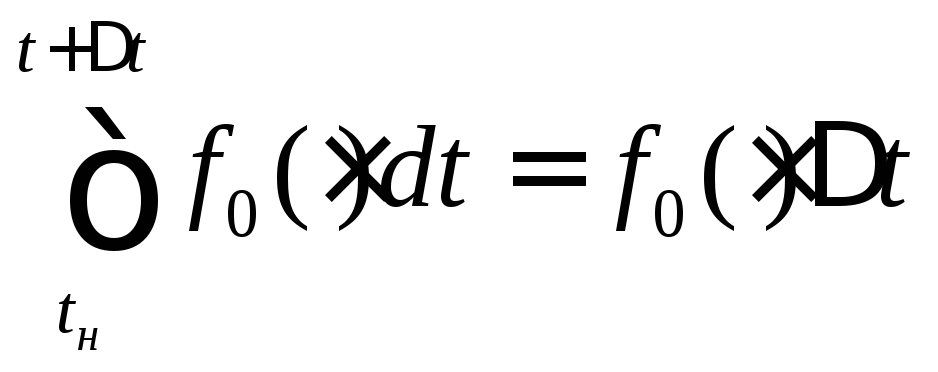
У такий спосіб

Приймемо допущення, що функція має частинні похідні по всіх координатахі за часом.

Тоді, розклавши в ряд Тейлора, одержимо

Згідно (3.1), запишемо

Тоді (3.7) приймає наступний вид

Підставимо (3.8) в (3.6) і одержимо

Беручи до уваги, що іне залежать від, (3.9) можна перетворити до виду

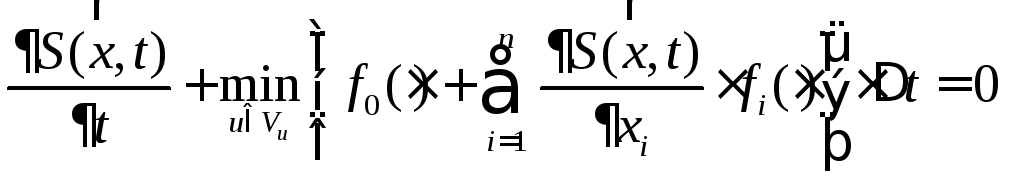
У результаті одержуємо

Або у векторній формі

Це рівняння в частинних похідних, називається рівнянням Беллмана. Рівняння Беллмана  аналітичний вираз принципу оптимальності для безперервних процесів. Він обґрунтований лише за умови, що існують частинні похідні функції по всіх координатахі часу. Випадки, коли це допущення не виконується, зустрічаються досить часто. Наприклад, допущення не виконується для лінійних систем у точках, що належить лінії (поверхні) перемикання.

За допомогою рівняння (3.11) можуть бути отримані оптимальні керування й траєкторії. Однак процедура аналітичного рішення рівняння в частинних похідних, ускладненого умовою мінімуму, представляє більші труднощі.