3.3.1. Решение типовых примеров заданий 6, 7 ргр

1. Привести к каноническому виду уравнение окружности . Найти координаты ее центра, радиус и построить окружность.

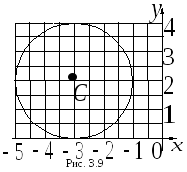Решение. Приведем уравнение к каноническому виду: прибавим и вычтем из него квадраты половин коэф-

фициентов при неизвестных и,

то есть и, а

затем выделим полные квадраты

;

,

следовательно, центр окружности нахо-

дится в точке , а радиус.

Ответ: .

2. Составить уравнение геометрического места точек, отношение расстояний которых от точкик расстоянию до прямойравно числу. Полученное уравнение привести к каноническому виду. Найти полуосии, координаты фокусови построить кривую.

Решение. Построим точкуи прямую. Пустьпроизвольная точка искомого геометрического места точек. Опустим перпендикуляр на прямуюи определим координаты точки. Так как точкалежит на указанной прямой, то ее абсцисса равна 6, а ордината – ординате точки(рис. 3.10). По условию задачи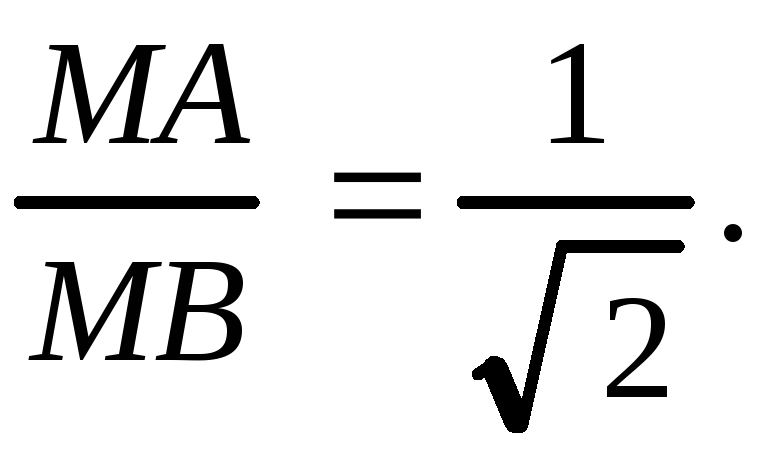

;.

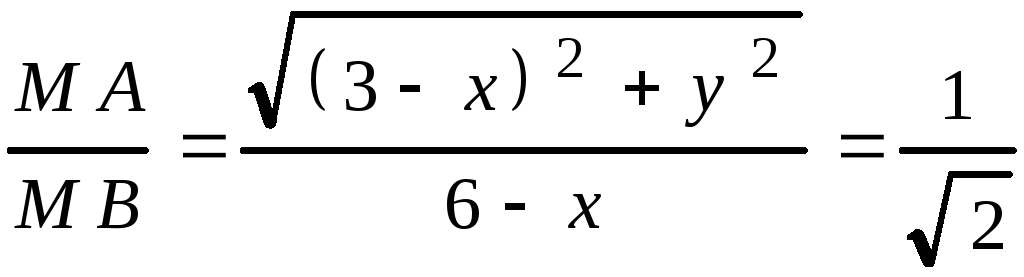Возведем обе части равенства в квадрат и выполним преобразования

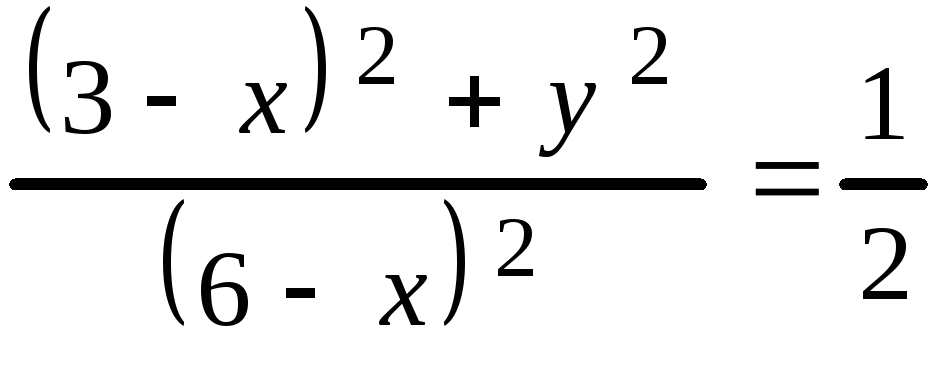
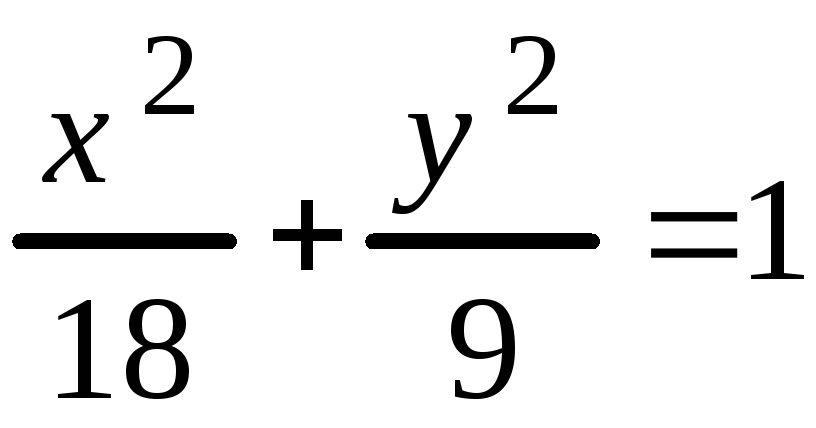– каноническое уравнение эллипса.

;;

Рис. 3.10

Ответ: Эллипс; ,;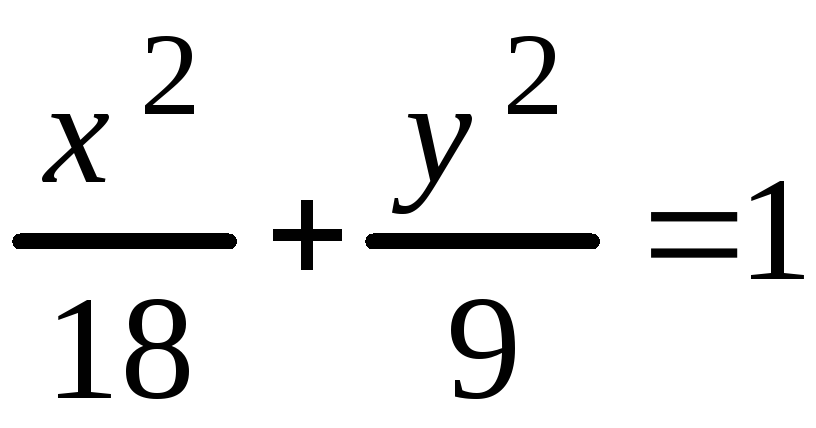

3. Составить каноническое уравнение геометрического места точек, отношение расстояний которых от точки к расстоянию до прямойравно. Найти координаты фокусов, вершин, эксцентриситет, и уравнения асимптот кривой. Определить точки пересечения кривой с окружностью, центр которой находится в начале координат, а окружность проходит через ее фокусы. Построить асимптоты, кривую и окружность.

Решение. 1) Построим точкуи прямую. Пусть произвольная точка искомого геометрического места точек (рис.3.11).

Соединим точки и, а затем проведем перпендикулярна прямую. Так как точкалежит на указанной прямой, то ее абсцисса, а ордината равна ординате точки, то есть.

По условию задачи Из рисунка находим

; .

Возведем обе части полученного равенства в квадрат и выполним преобразования

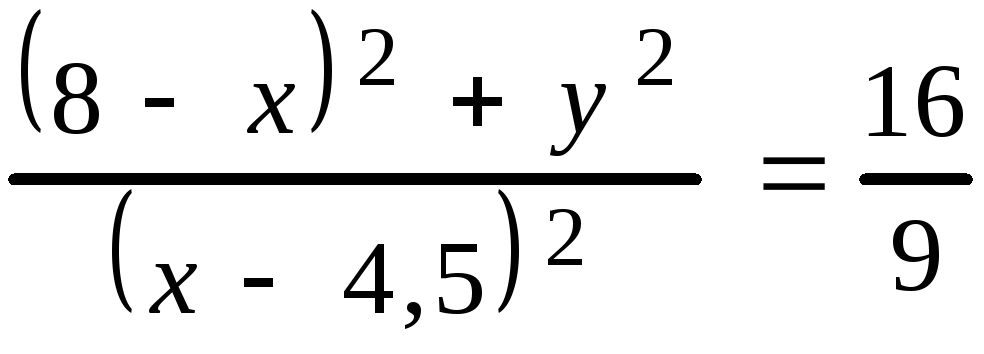
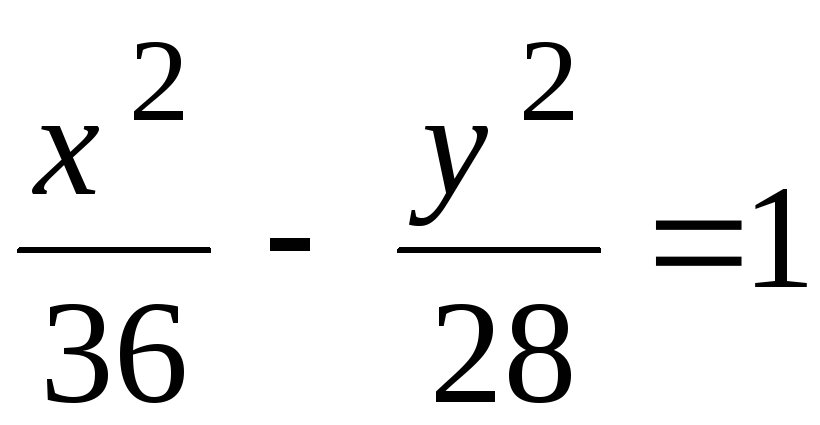– каноническое уравнение гиперболы.

Значит, полуоси гиперболы: ;

Найдем координаты фокусов гиперболы и радиус окружности

.

Определим координаты ее вершин .

Вычислим эксцентриситет гиперболы: .

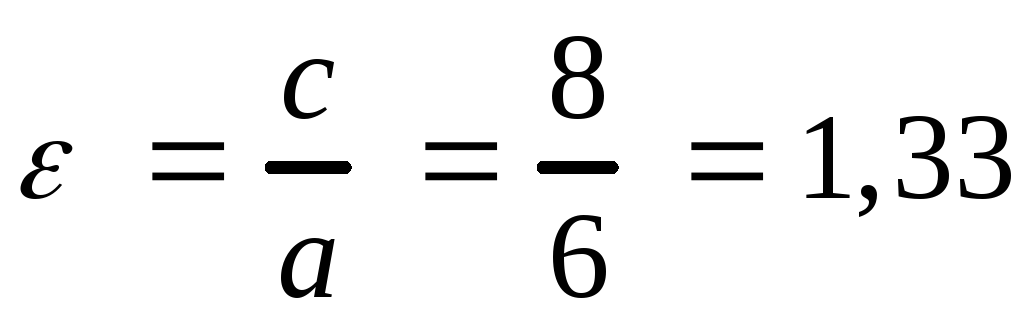Найдем уравнения асимптот ;.

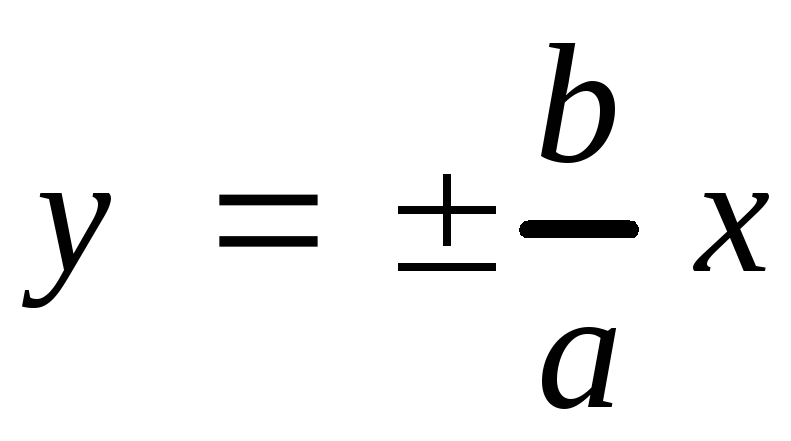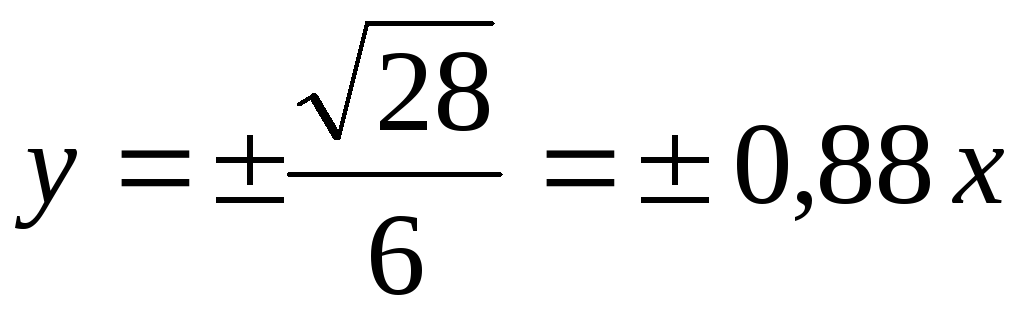Запишем уравнение окружности .

Для нахождения ее точек пересечения с гиперболой решим систему уравнений

.

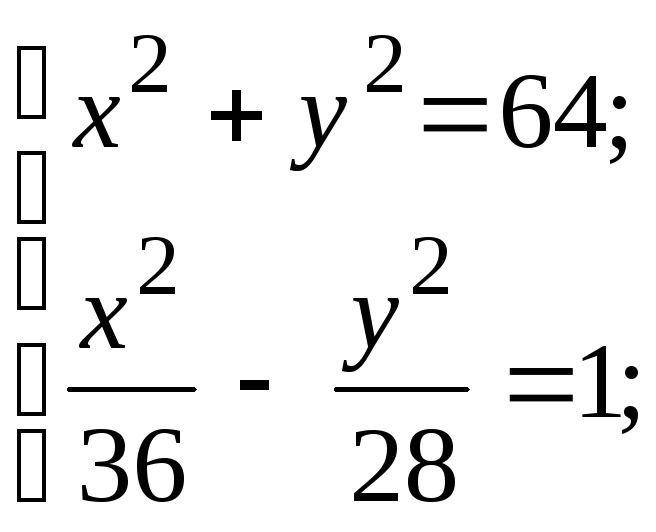
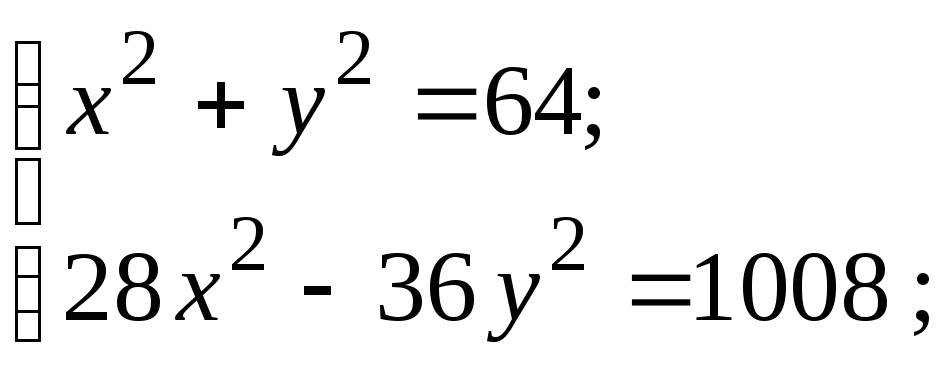
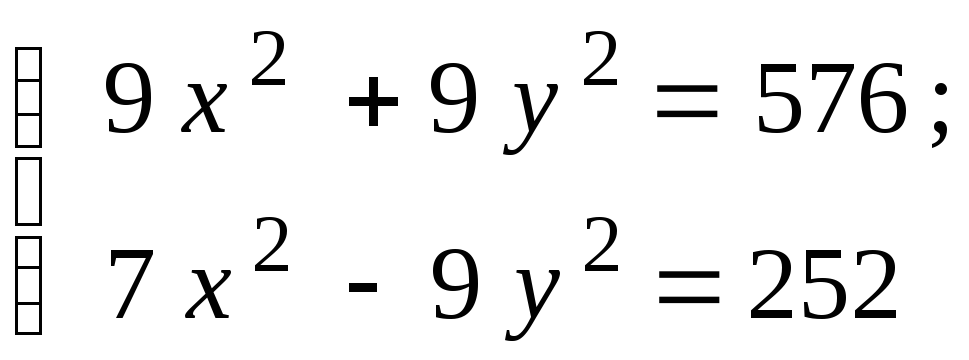
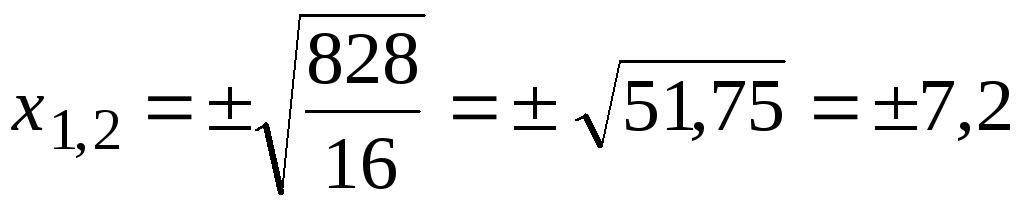Подставляя полученное значение в уравнение окружности, находим

.

Построим окружность и гиперболу

Рис. 3.11

4. Привести уравнение кривойк каноничес-кому виду. Найти параметркривой, координаты вершины, фокусаи уравнение директрисы. Построить кривую и ее директрису.

Решение. Прибавим и вычтем в левой части уравнения половину квадрата коэффициента передквадрат и преобразуем полученное уравнение

.

Сравнивая полученное уравнение с каноническим уравнением параболы (3.34), находим;;.

Координаты фокуса определяются, как

;, т.е..

Уравнение директрисы;.

Рис.3.12