
- •ВыСшая математика
- •Линейная, векторная алгебра
- •И аналитическая геометрия
- •Методические указания
- •3. Аналитическая геометрия на плоскости …………… 23
- •1. Линейная алгебра
- •1.1. Определители. Вычисление определителей
- •1.2. Матрицы и их свойства
- •1.3. Решение систем линейных уравнений
- •1.4. Решение типовых примеров задания 1 ргр
- •2. Векторная алгебра
- •2.1. Векторные и скалярные величины. Разложение вектора по координатным осям
- •2.2. Скалярное произведение двух векторов
- •. Условие параллельности и перпендикулярности векторов.
- •2.3.1. Решение типовых примеров задания 3 ргр
- •2.4. Смешанное произведение трех векторов
- •2.4.1. Решение типовых примеров задания 4 ргр
- •3. Аналитическая геометрия на плоскости
- •3.1. Длина и направление отрезка. Деление отрезка а заданном отношении. Площадь треугольника.
- •3.2. Прямая линия на плоскости
- •. Уравнение прямой с заданным угловым коэффициентом , (3.8)
- •. Уравнение прямой в отрезках на осях
- •Условие параллельности прямых
- •3.3. Кривые второго порядка в прямоугольной системе координат
- •3.3.1. Решение типовых примеров заданий 6, 7 ргр
- •3.4. Кривые второго порядка в полярной системе координат. Параметрические уравнения плоских кривых
- •Некоторые типы кривых на плоскости, заданных
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость . Основные уравнения плоскости
- •2. Направляющие косинусы нормали определяются по формулам
- •3. Условие параллельности плоскостей
- •4.1.1. Решение типовых примеров задания 8 ргр
- •4.2. Прямая линия в пространстве. Пересечение прямой и плоскости
- •4.2.1. Решение типовых примеров заданий 9, 10 ргр
- •Задания расчетно-графической работы №1 Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Формулы элементарной математикИ
- •7. Формулы двойного угла
- •8. Формулы понижения степени
- •9. Преобразование произведения тригонометрических функций в сумму
- •Приложение 4 Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Расчетно-графическая работа
3.3. Кривые второго порядка в прямоугольной системе координат
![]() Окружностьюназывают
геометрическое место точек, равноуда-ленных
от данной точки, называемой центром
окружности.
Окружностьюназывают
геометрическое место точек, равноуда-ленных
от данной точки, называемой центром
окружности.
Уравнение окружности имеет вид
![]() , (3.20)
, (3.20)
где
![]() координаты ее центра,
координаты ее центра,![]() радиус окружности .
радиус окружности .
![]() Эллипсом называется
геометрическое место точек, сумма
расстояний которых до двух данных точек
плоскости, называемых фокусами, есть
величина постоянная, большая, чем
расстояние между фокусами
Эллипсом называется
геометрическое место точек, сумма
расстояний которых до двух данных точек
плоскости, называемых фокусами, есть
величина постоянная, большая, чем
расстояние между фокусами![]() ,
,![]() const (рис. 3.5).
const (рис. 3.5).
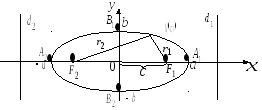
Рис. 3.5
Каноническое уравнение эллипса имеет вид
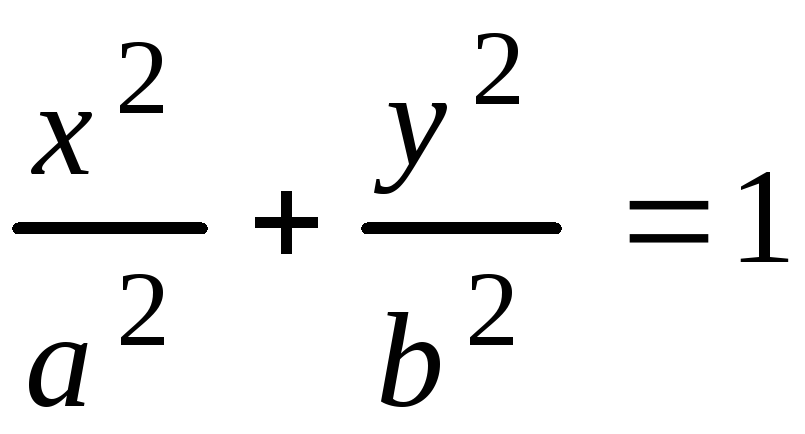 , (3.21)
, (3.21)
где
![]() большая и малая полуоси эллипса.
большая и малая полуоси эллипса.
Если фокусы эллипса расположены на оси
![]() ,
то их координаты
,
то их координаты![]() и
и![]() ,
и фокусное расстояние связано с полуосями
эллипса соотношением
,
и фокусное расстояние связано с полуосями
эллипса соотношением![]() .
(3.22)
.
(3.22)
Эллипс пересекает ось
![]() в точках
в точках![]() ,
,![]() ,
ось
,
ось![]() в точках
в точках![]() ,
,![]() .
Эти точки называютсявершинами
эллипса.Величины
.
Эти точки называютсявершинами
эллипса.Величины![]() и
и![]() называются соответственнобольшой
и малой осями эллипса.
называются соответственнобольшой
и малой осями эллипса.
Мера отклонения эллипса от окружности
характеризуется величиной
![]() ,
которая называетсяэксцентриситетом
эллипса и равна отношению
половины его фокального расстояния к
длине большой полуоси
,
которая называетсяэксцентриситетом
эллипса и равна отношению
половины его фокального расстояния к
длине большой полуоси
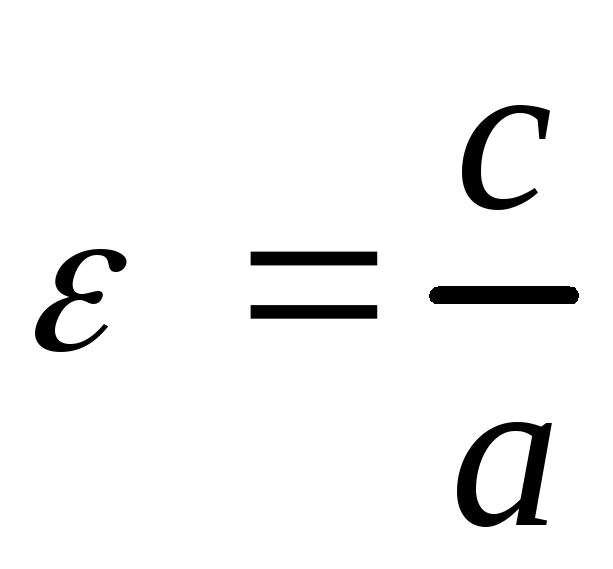 . (3.23)
. (3.23)
Поскольку у эллипса
![]() ,
то эксцентриситет любого эллипса
,
то эксцентриситет любого эллипса![]() .
.
Директрисами эллипса называются
прямые![]() ,
параллельные его малой оси и отстоящие
от нее на расстоянии
,
параллельные его малой оси и отстоящие
от нее на расстоянии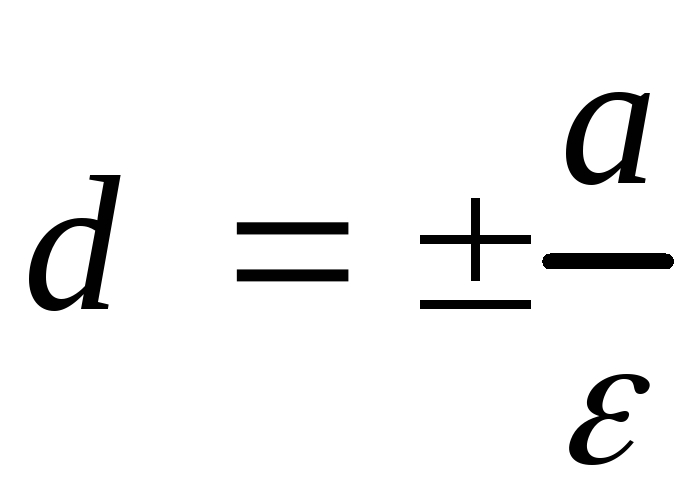 .
.

![]() Гиперболойназывается геометрическое
место точек, абсолютная величина разности
расстояний которых до двух данных точек
плоскости, называемых фокусами, есть
величина постоянная, меньшая чем
расстояние между фокусами
Гиперболойназывается геометрическое
место точек, абсолютная величина разности
расстояний которых до двух данных точек
плоскости, называемых фокусами, есть
величина постоянная, меньшая чем
расстояние между фокусами![]() ,
,![]() const (рис. 3.6).
const (рис. 3.6).
Рис. 3.6
Каноническое уравнение гиперболы имеет вид
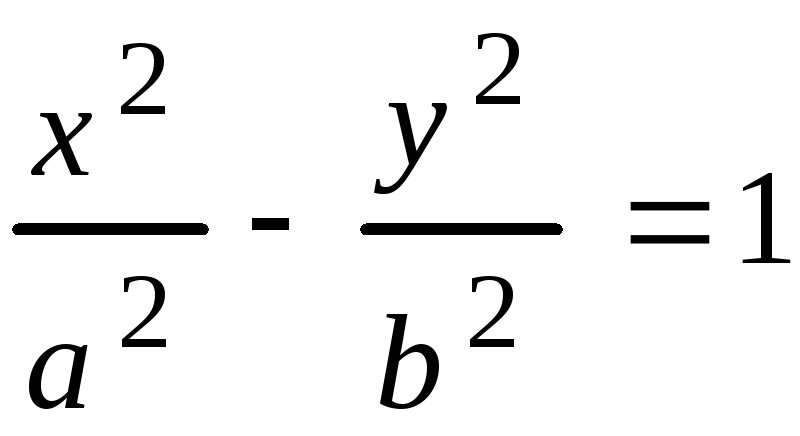 , (3.24)
, (3.24)
где
![]() действительная полуось;
действительная полуось;![]() мнимая полуось гиперболы.
мнимая полуось гиперболы.




 Прямые,
проходящие через центр симметрии, такие,
что если точка
Прямые,
проходящие через центр симметрии, такие,
что если точка![]() двигаясь по гиперболе, неограниченно
удаляясь от вершины неограниченно
приближаясь к одной из них, называются
асимптотами гиперболы.
двигаясь по гиперболе, неограниченно
удаляясь от вершины неограниченно
приближаясь к одной из них, называются
асимптотами гиперболы.
Уравнения асимптот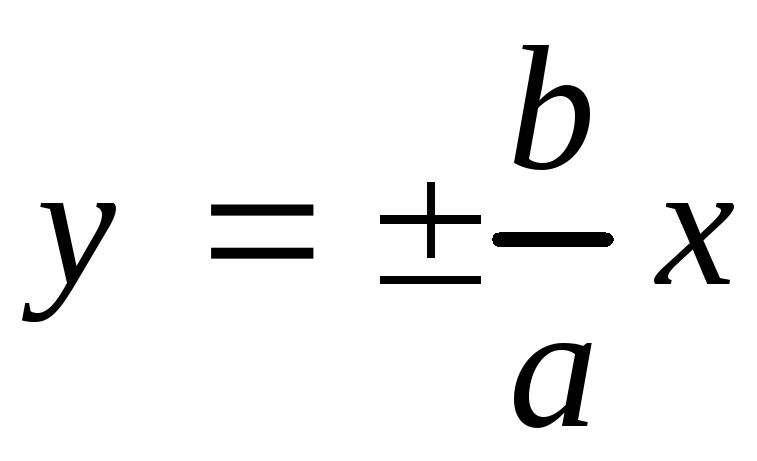 . (3.25)
. (3.25)
Если фокусы гиперболы расположены на
оси
![]() ,
то их координаты
,
то их координаты![]() и
и![]() ,
и фокусное расстояние связано с
действительной
,
и фокусное расстояние связано с
действительной![]() и мнимой
и мнимой![]() полуосями соотношением
полуосями соотношением
![]() .
(3.26)
.
(3.26)
Гипербола пересекает ось
![]() в точках
в точках![]() ,
,![]() .
Эти точки называютсявершинами
гиперболы.
.
Эти точки называютсявершинами
гиперболы.
Эксцентриситетом гиперболы![]() называется отношение фокусного расстояния
гиперболы к ее действительной оси, то
есть
называется отношение фокусного расстояния
гиперболы к ее действительной оси, то
есть
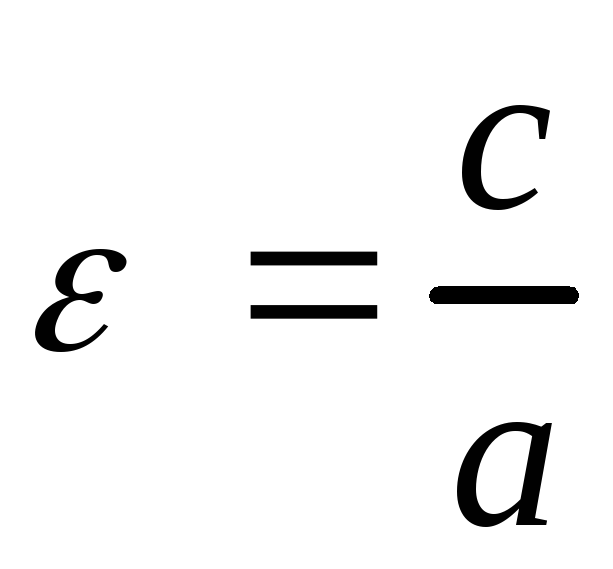 . (3.27)
. (3.27)
Поскольку у гиперболы
![]() ,
то эксцентриситет гиперболы
,
то эксцентриситет гиперболы![]() .
.
Директрисами гиперболыназываются
прямые![]() ,
параллельные мнимой оси и отстоящие от
нее на расстоянии
,
параллельные мнимой оси и отстоящие от
нее на расстоянии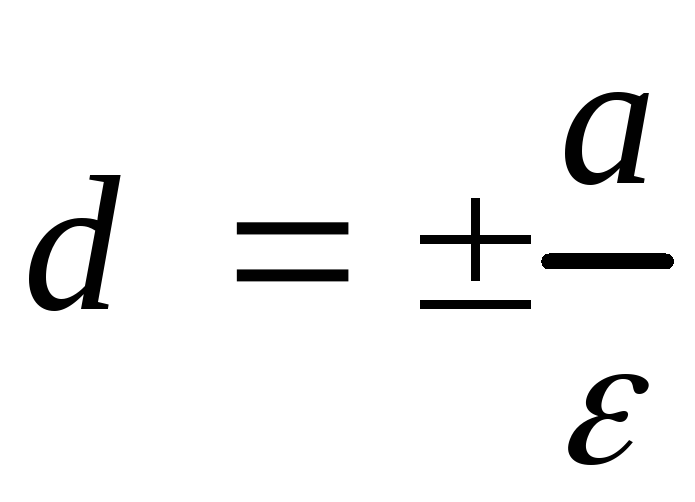 .
.
![]() Параболойназывается
геометрическое место точек, равноуда-ленных
от данной точки, называемой фокусом и
от данной прямой, называемой директрисой
и не проходит через фокус (рис. 3.7).
Параболойназывается
геометрическое место точек, равноуда-ленных
от данной точки, называемой фокусом и
от данной прямой, называемой директрисой
и не проходит через фокус (рис. 3.7).
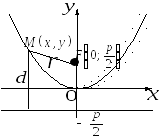
Рис. 3.7.
Каноническое уравнение параболы, ось
симметрии которой парал-лельна оси
![]() а вершина совпадает с началом координат,
имеет вид
а вершина совпадает с началом координат,
имеет вид
![]() , (3.28)
, (3.28)
где
![]() параметр параболы, равный расстоянию
от фокуса до директрисы.
параметр параболы, равный расстоянию
от фокуса до директрисы.
Фокальный радиус любой точки параболы
![]() вычисляется по формуле
вычисляется по формуле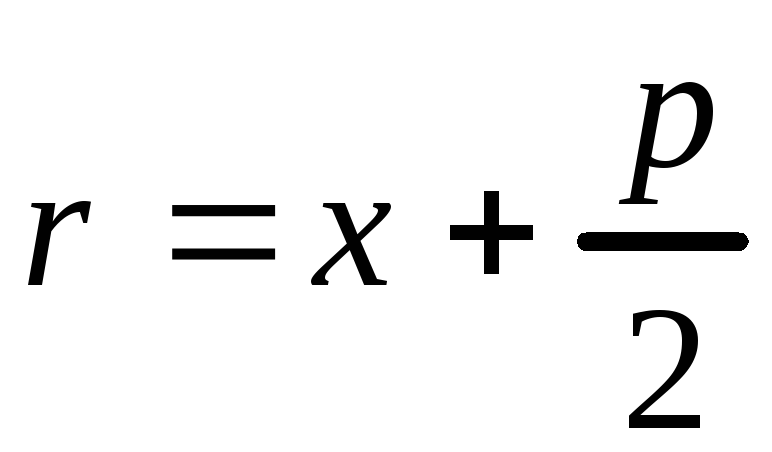 . (3.29)
. (3.29)
У параболы один фокус, следовательно,
и одна директриса
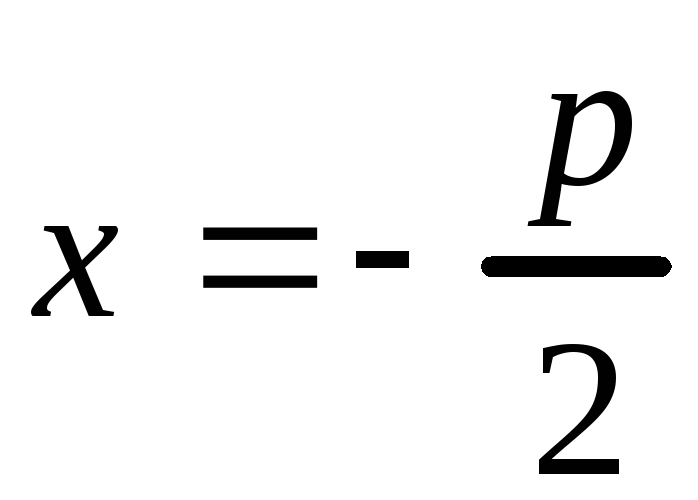 .
.
Эксцентриситет параболы равен
отношению расстояния любой ее точки от
фокуса к расстоянию до директрисы. На
основании определения параболы имеем,
что эксцентриситет любой параболы равен
единице![]() .
.
Уравнение
![]() ,
,![]() ,
является каноническим уравнением
параболы, с ветками, направленными вверх
(рис. 3.8,а), а уравнение
,
является каноническим уравнением
параболы, с ветками, направленными вверх
(рис. 3.8,а), а уравнение![]() ,
,![]() – уравнением параболы, с ветками
направленными вниз (рис. 3.8,б).
– уравнением параболы, с ветками
направленными вниз (рис. 3.8,б).

Рис. 3.8
П



 арабола,
каноническое уравнение которой
арабола,
каноническое уравнение которой![]() ,
,![]() ,
симметрична оси
,
симметрична оси![]() и расположена слева оси
и расположена слева оси![]() ,
(рис. 3.8,в), а парабола
,
(рис. 3.8,в), а парабола![]() ,
,![]() – справа оси
– справа оси![]() (рис. 3.8,г).
(рис. 3.8,г).
Если парабола симметрична оси
![]() координаты вершины параболы
координаты вершины параболы![]() то уравнение имеет вид
то уравнение имеет вид
![]() . (3.30)
. (3.30)
