2. Векторная алгебра

2.1. Векторные и скалярные величины. Разложение вектора по координатным осям

. Основные определения.

Величина называется скалярной, если она определяется заданием ее числового значения, ивекторной, если для ее определения задается еще и ее направление.

Два вектора называются коллинеарными, если они расположены на параллельных прямых (или на одной прямой), независимо от того, направ-лены ли они одинаково или их направления противоположны.

Если векторы лежат в одной плоскости или в плоскостях, параллельных между собой, то они называются компланарными.

Вектор, модуль которого равен 1, называется единичнымвектором.

. Разложение вектора по базису ,,.

Возьмем прямоугольную систему координат в пространстве и вместе с ней три единичных вектора, ,,, начало которых совпадают с началом координат и направленные, соответ-ственно по осям,,(рис. 2.1).

Система трех векторов ,,, называется декартовым прямоугольным базисом.

Всякий вектор в пространстве можно представить как сумму трех векторов, один из которых расположен на оси , второй на осии третий – на оси

, (2.1)

где единичные векторы, направленные вдоль координатных осей.

Модуль вектора равен

. (2.2)

. Действия над векторами.

Если и– координаты начала и конца вектора, то:

– координаты вектора проекции

; (2.3)

– модуль вектора

; (2.4)

– его направляющие косинусы

;. (2.5)

2.2. Скалярное произведение двух векторов

.Скалярным произведениемдвух векторовиназывается число, равное произведению их модулей на косинус угла между ними:

. (2.6)

Углом между векторами иназывается

угол , на который следует повернуть один из

векторов для того, чтобы их направления совпали

(рис. 2.2.)

. Выражение скалярного произведения через проекции перемножаемых векторов.

Если векторы изаданы своими проекциями на оси координат

,,

то скалярное произведениеэтих векторов равно сумме произведений одноименных проекций перемножаемых векторов.

. (2.7)

. Угол между векторами. Из уравнения (2.6) с учетом (2.7) следует

. (2.8)

. Условие параллельности и перпендикулярности векторов.

Если ,, то:

– условие параллельностивекторов

, (2.9)

– условие перпендикулярностивекторов

. (2.10)

.Механический смысл скалярного произведения

Из физики известно, что работа, силыпри перемещении материальной точки с начала в конец вектора, который образует с векторамугол(рис. 2.3)

равна ,

или, согласно (2.6) .

Поэтому работа равна скалярному произведению вектора силы на вектор перемещения . В этом сутьмеханического смысла скалярного произведения.

2.2.1. Решение типовых примеров задания 2 РГР

1. Найти внутренние углы,итреугольника, с вершинами,,и убедиться, что их сумма равна.

Решение. Найдем координаты векторов,,, согласно (2.3) и противоположные им вектора,,,учитывая, что составляющие последних имеют знаки, противоположные составляющим основных векторов

.

,;

, ;

, .

Вычислим длины сторон треугольника по формуле (2.4):

.

;

;

.

Найдем косинусы углов между векторами по формуле (2.8):

.

.

.

.

Проверка:.

Ответ: ; ; .

2.3. Векторное произведение двух векторов

Тройка некомпланарных векторов называетсяправой,если при вращении буравчика в направлении от векторак векторунаправление поступательного движения буравчика образует острый угол с направлением вектора. Если же угол тупой, то тройка называетсялевой.

.Векторным произведением двух векторовназывается вектор, который удовлетворяет следующим условиям:

1) длина вектора равна, где; (2.11)

2) вектор перпендикулярный каждому из векторов, т.е.и;

3) вектор , направлен так, что векторы,иобразуют правую тройку векторов. Векторное произведение обозначают одним из символов:

.

. Есливекторызаданысвоими проекциями на координатные оси и, товекторное произведение определяется формулой. (2.12)

. Геометрический смысл векторного произведения.

М

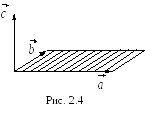одульвекторного произве-дения равен площади параллелограмма, построенного на векторахи, отнесенных к общему началу, т.е.

. (2.13)

. Приложения.

1. Момент силы , приложенной к

точке относительно точкиО, равен

векторному произведению силы на

вектор :

.

2. Скорость точкитвердого тела, которая вращается с угловой скоростьювокруг неподвижной оси, определяется формулой Эйлера

.

3. Если электрон, с зарядом движется со скоростьюв магнитном поле постоянной напряженности, то на электрон действует сила

.

4. Площадь , равна половине площади параллелограмма

. (2.14)