1.3. Решение систем линейных уравнений

Рассмотрим три способа решения систем линейных уравнений: по формулам Крамера, матричным способом, методом Гаусса.

Пусть дана система линейных уравнений

(1.5)

. При решении системы (1.5)по формулам Крамера, неизвестные находятся из соотношений:

,, …,, (1.6)

где определитель системы,,, …,определители неизвестных, которые получаются иззаменой его первого, второго и т.д. столбца соответственно столбцом свободных членов.

. Решение системы линейных уравнений (1.5)матричным способом.

Если ввести матричные обозначения

,,,

то систему можно записать матричным уравнением

. (1.7)

Решение системы матричным методом определяется соотношением

. (1.8)

То есть, чтобы решить систему (1.5), необходимо найти матрицу , обратную до матрицы системы, и умножить ее на матрицу свободных членов (см. раздел 1.2).

Формулу (1.8) называют матричной записью решения системы(1.5) илирешением матричного уравнения(1.7).

. Решение систем линейных уравненийметодом Гаусса.

Одним из наиболее простых методов решения систем линейных уравнений есть метод непосредственного исключения неизвестных или метод Гаусса. Этот метод предложен К. Гауссом и базируется на элементарных преобразованиях системы уравнений, или проще, расши-ренной матрицы.

Расширенной матрицей системы линейных уравнений (1.5) называют матрицу коэффициентов системы с добавленным еще одним столбцом свободных членов, который отделяется черточкой, т.е.

. (1.9)

Под элементарными преобразованиями расширенной матрицы подразумевается следующее:

1. перестановка любых двух строк матрицы;

2) умножение какой-либо строки матрицы на любое, отличное от нуля число;

3) прибавление к любой строке матрицы соответствующих членов другой строки, умноженных на одно и то же число.

Идея метода Гауссасостоит в том, чтобы с помощью элементарных преобразований привести расширенную матрицу к равносильной матрице треугольного (или трапециевидного) вида.

Затем, по полученной расширенной матрице восстанавливается равносильная система линейных уравнений, из которой последовательно находятся все неизвестные.

1.4. Решение типовых примеров задания 1 ргр

1. Решить систему алгебраических уравнений

а) по формулам Крамера,б) матричным способом,в) методом Гаусса.

Решение.

а) Решим задачу по формулам Крамера, которые имеют вид

,,,

где – определитель системы уравнений;,,– определители неизвестных, полученные иззаменой его первого, второго и третьего столбца соответственно, столбцом свободных членов.

Запишем определители ,,,и раскроем их:

Теперь найдем неизвестные ,,по формулам (1.6)

;;.

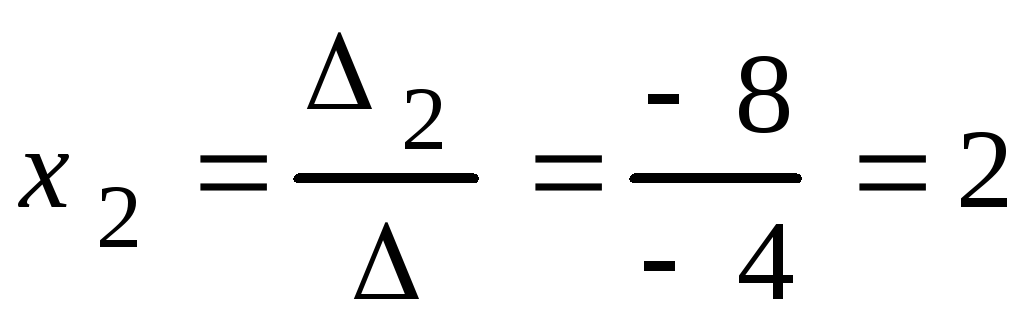Ответ:;;.

б) Решим систему уравнений матричным способом.

Обозначим через матрицу исходной системы уравнений, черезвектор-столбец неизвестных и черезвектор-столбец свободных членов:

, ,

Если система линейных уравнений в матричном виде записывается , то матрица неизвестных находится из уравнения.

Для нахождения матрицы неизвестных найдем обратную матрицу (см. раздел 1.2) и умножим ее на матрицу-столбец свободных членов.

Так как матрица невырожденная, (как было определено ранее, (), то для нее существует обратная матрица.

Обратную матрицу найдем в следующей последовательности:

1) Запишем транспонированную матрицу , т.е. матрицу, в которой строки матрицызаменены ее столбцами с тем же номером

.

Обратную матрицу можно получить по формуле:

,

где – определитель матрицы,– алгебраические дополнения (миноры), равные определителям, которые получаются с помощью вычеркивания-й строки и-го столбца транспонированной матрицы, взятые со знаком.

Найдем алгебраические дополнения транспонированной матрицы :

;;;

;;;

;;.

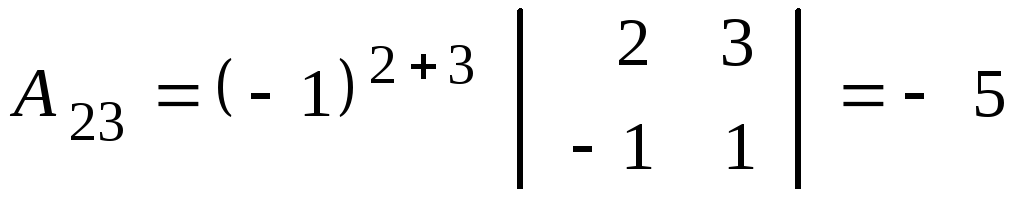Таким образом, ,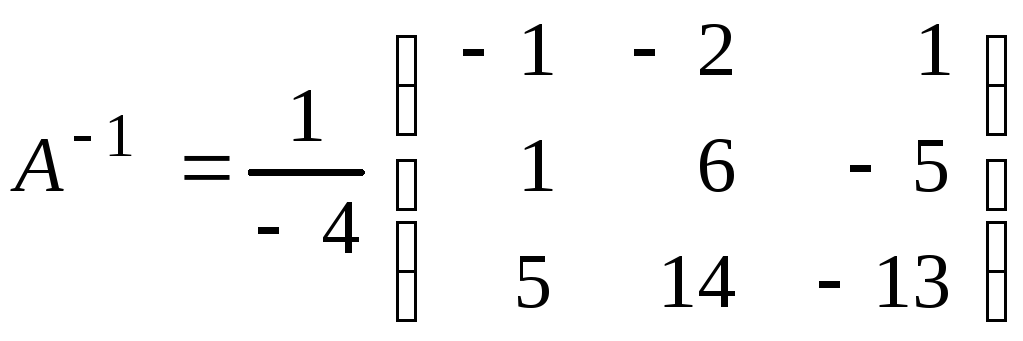

а решение системы уравнений равно

.

Найдем значения , , .

= ;

= ;

=.

Подставляя вместо , , числовые значения, получим:

.

Ответ:;;.

в) Решим систему уравнений методом Гаусса.

Запишем расширенную матрицу системы

и сделаем элементарные преобразования.

Сделаем коэффициент равным единице и обнулим коэффициенты,и.

Для этого:

а) поменяем местами первую и вторую строки, а затем вычтем из первой строки вторую. Результат запишем на место первой строки

~

~

б) вычтем из второй строки первую, умноженную на 2. Результат запишем на место второй строки

~

~

в) вычтем из третей строки первую, умноженную на 4. Результат запишем на место третей строки

~

~

г) умножим вторую строку на 19, а третью на 13. Затем вычтем из третей строки вторую и результат запишем на место третей строки

~

.

Осуществим обратный ход метода Гаусса, восстановив равносильную систему по расширенной матрице

Из последнего уравнения имеем .

Подставляем это значение во второе уравнение и находим

.

Подставляя значения ив первое уравнение находим:

.

Ответ:;;.