
- •ВыСшая математика
- •Линейная, векторная алгебра
- •И аналитическая геометрия
- •Методические указания
- •3. Аналитическая геометрия на плоскости …………… 23
- •1. Линейная алгебра
- •1.1. Определители. Вычисление определителей
- •1.2. Матрицы и их свойства
- •1.3. Решение систем линейных уравнений
- •1.4. Решение типовых примеров задания 1 ргр
- •2. Векторная алгебра
- •2.1. Векторные и скалярные величины. Разложение вектора по координатным осям
- •2.2. Скалярное произведение двух векторов
- •. Условие параллельности и перпендикулярности векторов.
- •2.3.1. Решение типовых примеров задания 3 ргр
- •2.4. Смешанное произведение трех векторов
- •2.4.1. Решение типовых примеров задания 4 ргр
- •3. Аналитическая геометрия на плоскости
- •3.1. Длина и направление отрезка. Деление отрезка а заданном отношении. Площадь треугольника.
- •3.2. Прямая линия на плоскости
- •. Уравнение прямой с заданным угловым коэффициентом , (3.8)
- •. Уравнение прямой в отрезках на осях
- •Условие параллельности прямых
- •3.3. Кривые второго порядка в прямоугольной системе координат
- •3.3.1. Решение типовых примеров заданий 6, 7 ргр
- •3.4. Кривые второго порядка в полярной системе координат. Параметрические уравнения плоских кривых
- •Некоторые типы кривых на плоскости, заданных
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость . Основные уравнения плоскости
- •2. Направляющие косинусы нормали определяются по формулам
- •3. Условие параллельности плоскостей
- •4.1.1. Решение типовых примеров задания 8 ргр
- •4.2. Прямая линия в пространстве. Пересечение прямой и плоскости
- •4.2.1. Решение типовых примеров заданий 9, 10 ргр
- •Задания расчетно-графической работы №1 Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Формулы элементарной математикИ
- •7. Формулы двойного угла
- •8. Формулы понижения степени
- •9. Преобразование произведения тригонометрических функций в сумму
- •Приложение 4 Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Расчетно-графическая работа
1. Линейная алгебра
1.1. Определители. Вычисление определителей
![]() .Определителем 2-го порядка
называется выражение вида
.Определителем 2-го порядка
называется выражение вида
 .
.
Определителем 3-го порядка называется число выражение вида
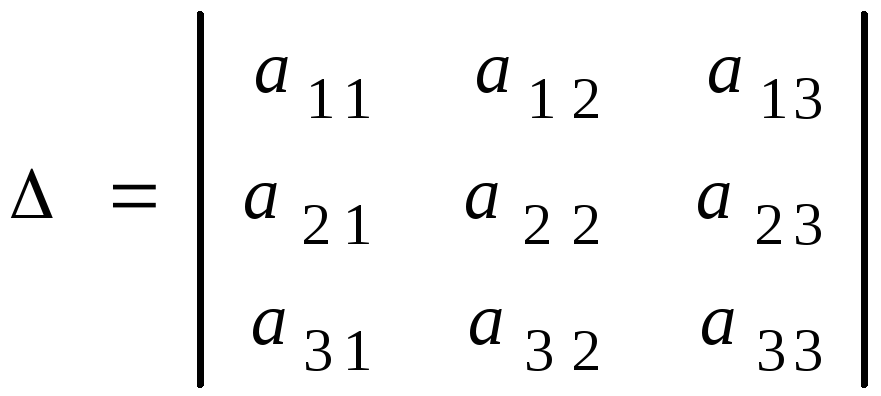 .
.
Определителем
![]() го
порядка называется выражение
вида
го
порядка называется выражение
вида
 .
.
Общее обозначение элементов определителя
![]() ,
где
,
где![]() номер строки,
номер строки,![]() номер
столбца,
номер
столбца,![]() ,
то есть элемент
,
то есть элемент![]() находится на пересечении
находится на пересечении![]() ой
строки и
ой
строки и![]() го
столбца.
го
столбца.
Диагональ, соединяющая левый верхний угол определителя с нижнем правым углом главной, а диагональ, соединяющая правый верхний угол с нижним левым углом определителя – побочной.
![]() .
Вычисление определителей.
.
Вычисление определителей.
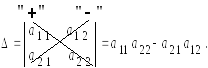 1.
Определители2-го
порядка вычисляются
по формуле
1.
Определители2-го
порядка вычисляются
по формуле
(1.1)
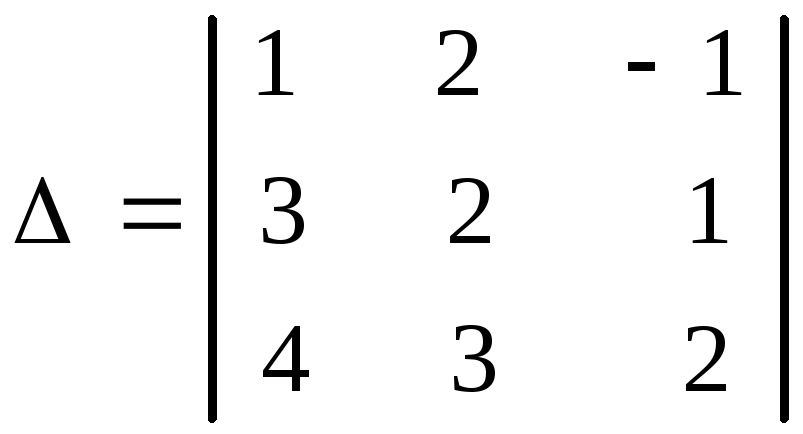
Пример 1.1. Вычислить определитель 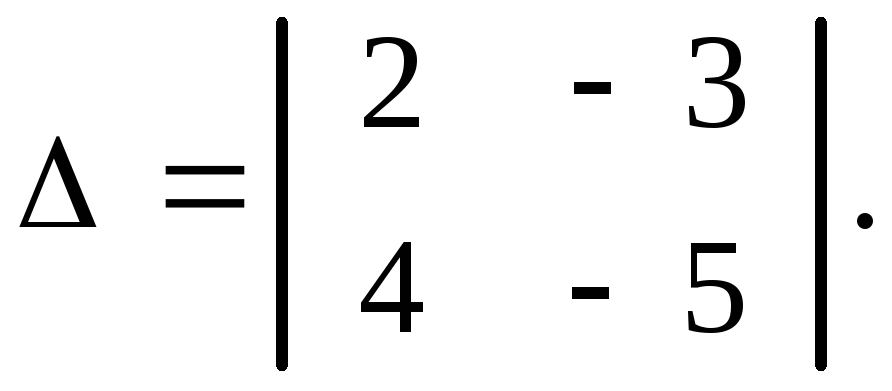
Решение.  .
.
2. Вычисление определителей3-го порядкапо правилу Саррюса или правилу треугольников.
При вычислении определителя 3-го порядка
по правилу Саррюса к нему
приписываются два первых столбца.Произведения
элементов, лежа-щих на диагоналях,
параллельных главной, берутся со знаком
«![]() »,
а эле-ментов, лежащих на диагоналях,
параллельных побочной – со знаком «
»,
а эле-ментов, лежащих на диагоналях,
параллельных побочной – со знаком «![]() ».
».
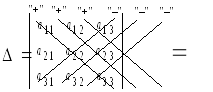
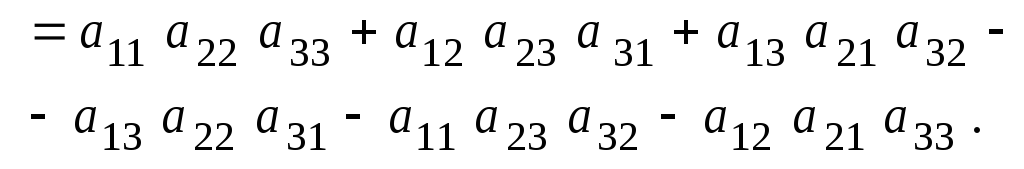 (1.2)
(1.2)
Определители 3-го порядка можно вычислять по правилу треугольников.
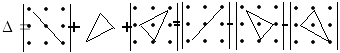 Произведения
элементов, расположенных на главной
диагонали и в вершинах треугольников
с основаниями параллельными ей, берутся
со знаком «
Произведения
элементов, расположенных на главной
диагонали и в вершинах треугольников
с основаниями параллельными ей, берутся
со знаком «![]() »,
а элементов, расположенных на побочной
диагонали и в вер-шинах треугольников
с основаниями параллельными ей, – со
знаком «
»,
а элементов, расположенных на побочной
диагонали и в вер-шинах треугольников
с основаниями параллельными ей, – со
знаком «![]() ».
».
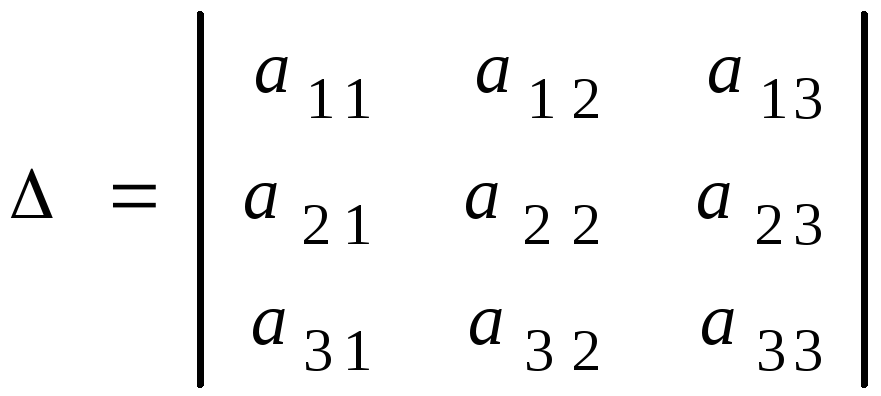
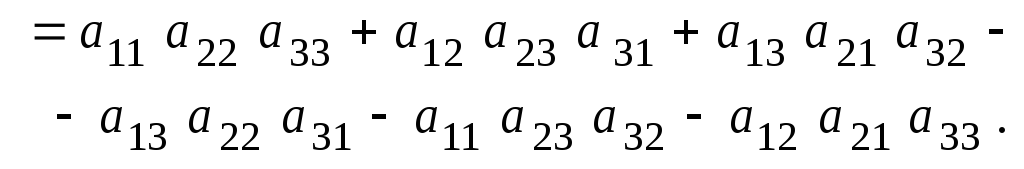
Пример 1.2. Вычислить определитель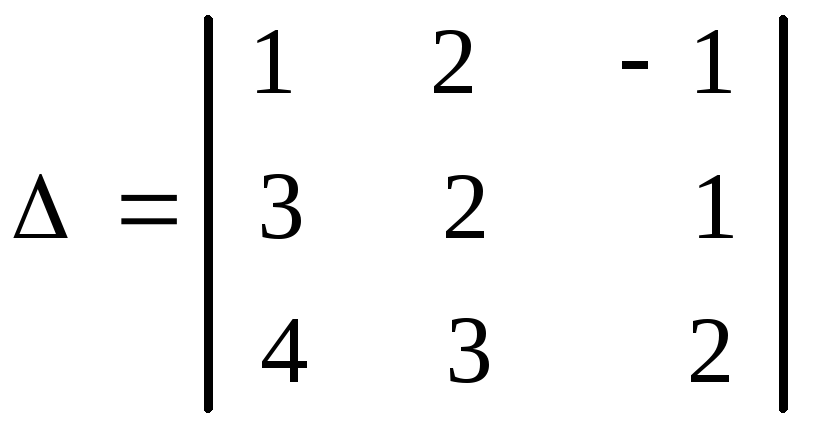
а) по правилу Саррюса;б) по правилу треугольников.
Решение. а) Вычислим определитель по правилу Саррюса
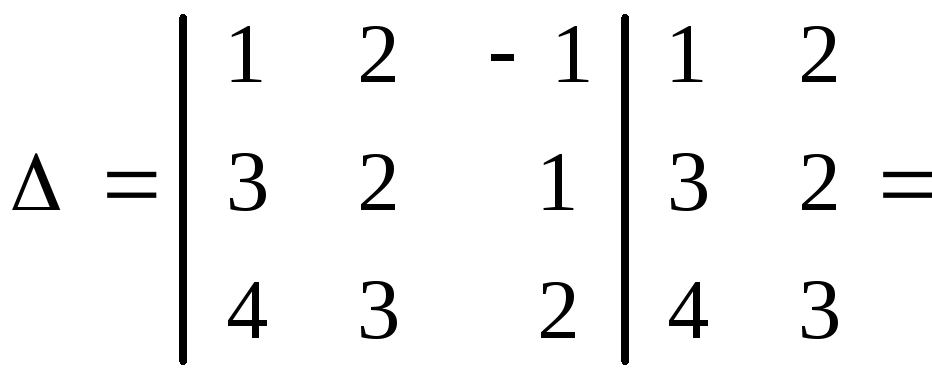
![]()
![]() .
.
б) Вычислим определитель по правилу треугольников
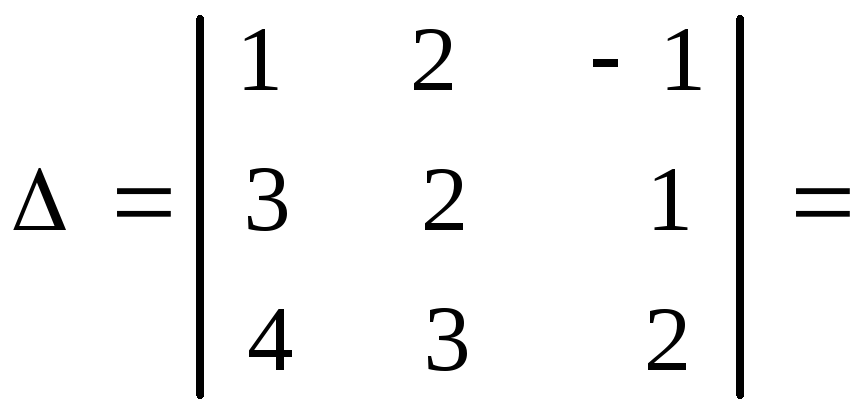
![]()
![]() .
.
3. Вычисление определителей разложением по элементам строки (или столбца).
а)
Минором
![]() соответствующим элементу
соответствующим элементу![]() определителя
определителя![]() го
порядка
го
порядка![]() называется определитель
называется определитель![]() го
порядка
го
порядка![]() ,
который получается из определителя
,
который получается из определителя![]() путем вычеркивания
путем вычеркивания![]() й
строки и
й
строки и![]() го
столбца, на пересечении которых находится
элемент
го
столбца, на пересечении которых находится
элемент![]() .
.
б)
Алгебраическим
дополнением
![]() элемента
элемента![]() определителя
определителя![]() называется его минор
называется его минор![]() ,
взятый со знаком
,
взятый со знаком![]() ,
т.е.
,
т.е.
![]()
![]() .
.
в) Всякий определитель равен сумме произведений элементов неко-торой строки (столбца) на алгебраические дополнения этих элементов.
Например, разложение определителя 3-го порядка по элементам первой строки имеет вид
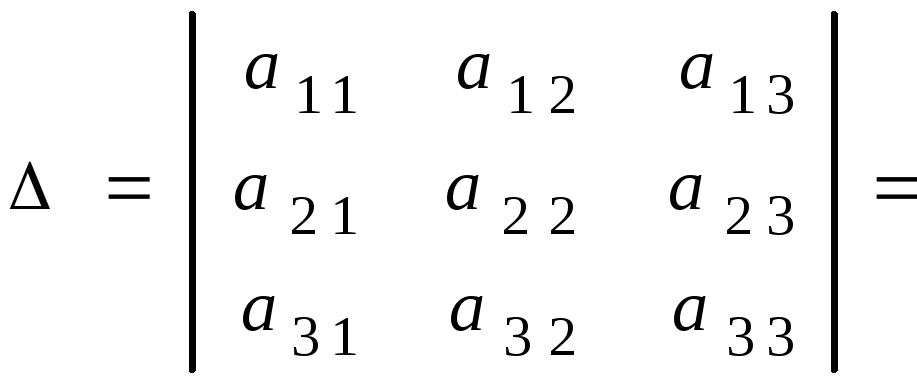 (1.3)
(1.3)
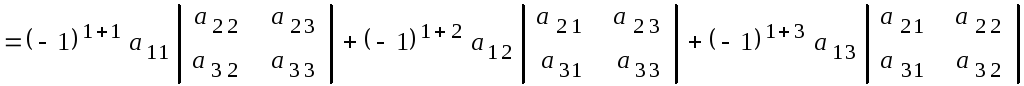 .
.
Пример 1.3. Вычислить определители разложением по элементам первой
строки:
 .
.
Решение.Разложим определители по элементам первой строки:
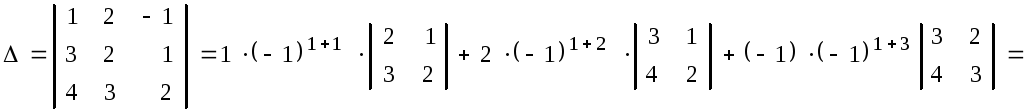
![]() .
.
1.2. Матрицы и их свойства
![]() .Матрицейразмера
.Матрицейразмера![]() называется прямоугольная таблица,
состоящая из элементов
называется прямоугольная таблица,
состоящая из элементов![]() ,
содержащая
,
содержащая![]() строк и
строк и![]() столбцов. Каждую такую таблицу заключают
в круглые скобки или двойные вертикальные
черточки и обозначают какой-либо большой
буквой латинского алфавита.
столбцов. Каждую такую таблицу заключают
в круглые скобки или двойные вертикальные
черточки и обозначают какой-либо большой
буквой латинского алфавита.
Например,
 ,
или
,
или .
.
В сокращенной записи матрица обозначается
![]() ;
или
;
или![]() ;
;![]() ;
;![]() .
.
Числа
![]() называются элементами матрицы, индекс
называются элементами матрицы, индекс![]() обозначает номер строки, а
обозначает номер строки, а![]() - номер столбца, на пересечении которых
стоит элемент.
- номер столбца, на пересечении которых
стоит элемент.
Матрица, в которой число рядков равно числу столбцов, называется квадратной.
Совокупность элементов квадратной матрицы, расположенных на отрезке, соединяющем левый верхний угол с правым нижним, называют главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним – побочной диагональю матрицы.
![]() .
Умножение матриц.
.
Умножение матриц.
1. Операция умножения
вводится только для согласованных
матриц. Матрица
![]() называетсясогласованной
с матрицей
называетсясогласованной
с матрицей
![]() ,
если количество столбцов матрицы
,
если количество столбцов матрицы![]() равно количеству строк матрицы
равно количеству строк матрицы![]() .
.
Заметим, что из
согласованности матрицы
![]() с
с![]() не следует
согла-сованность матриц
не следует
согла-сованность матриц
![]() с
с![]() .
.
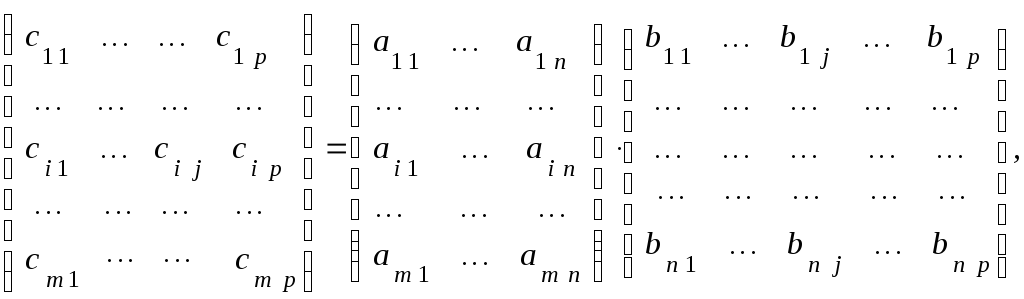

![]() и
и![]() ,заданных в определен-ном порядке (
,заданных в определен-ном порядке (![]() – первая,
– первая,![]() –
вторая) называется матрица
–
вторая) называется матрица![]() ,
каждый элемент которой
,
каждый элемент которой![]() равен сумме произведений элементов
равен сумме произведений элементов![]() ой
строки
ой
строки
матрицы
![]() на соответствующие элементы
на соответствующие элементы![]() го
столбца матрицы
го
столбца матрицы![]() :
:
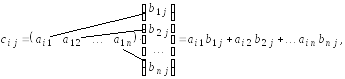
где
![]() ;
;![]() .
.
Пример 1.4.
Вычислить произведение матриц
![]() ,
если
,
если
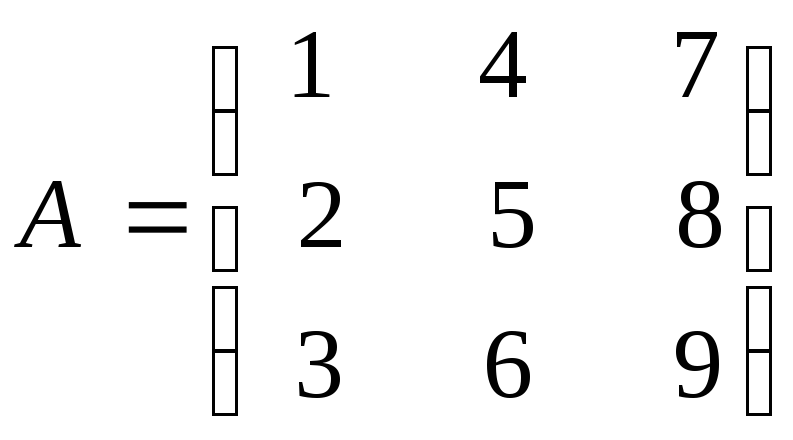 ;
;
![]() .
.
Решение.
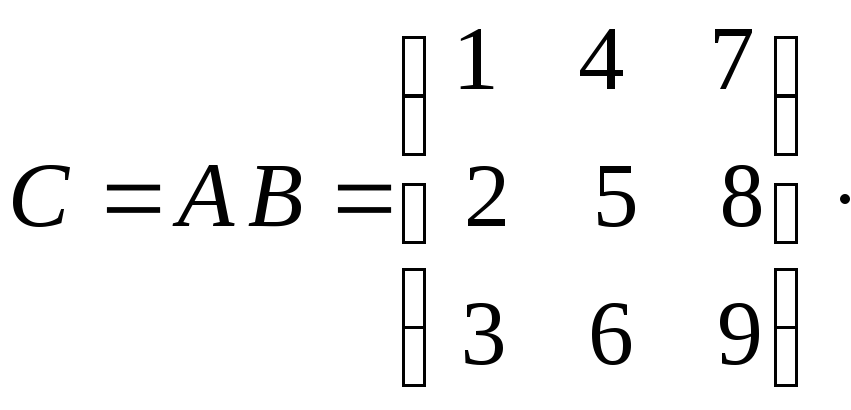
![]()
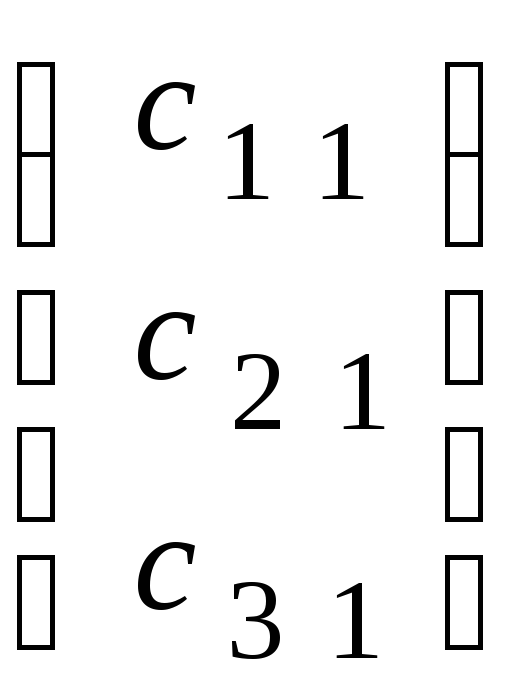 ,
,
где ![]()
![]() ;
;
![]() .
.
Таким образом, окончательно имеем:
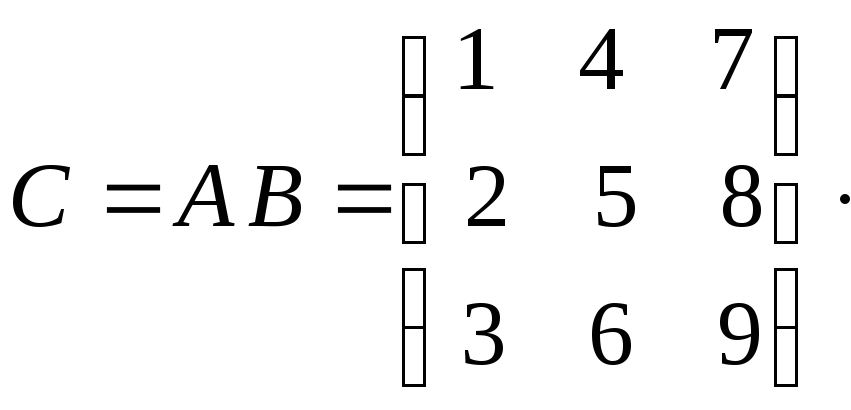
![]()
![]() .
.
![]() .
Транспонирование матрицы
.
Транспонирование матрицы
Транспонировать
матрицу
![]() значит поменять местами строки и столбцы
матрицы с сохранением их нумерации.
Транспонированная матри-ца обозначается
значит поменять местами строки и столбцы
матрицы с сохранением их нумерации.
Транспонированная матри-ца обозначается![]() .
.
Например,
 ,
,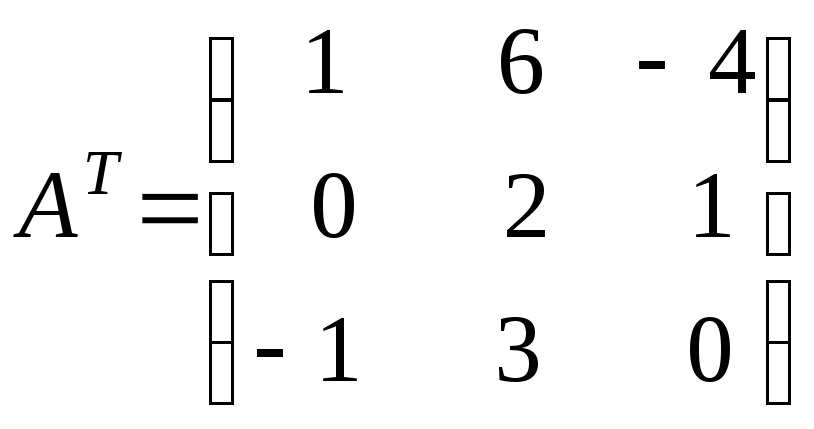 .
.
![]() .
Обратная матрица
.
Обратная матрица
Обратной
матрицей
по отношению к заданной квадратной
матрице
![]() называется такая квадратная матрица,
обозначаемая
называется такая квадратная матрица,
обозначаемая![]() ,
которая удовлетворяет равенствам
,
которая удовлетворяет равенствам
![]() и
и![]() .
.
Для нахождения
обратной матрицы
![]() ,
необходимо сначала вычис-лить определитель
матрицы
,
необходимо сначала вычис-лить определитель
матрицы![]() и убедится, что матрица невырожденная
и убедится, что матрица невырожденная![]() ,
затем записать транспонированную
матрицу
,
затем записать транспонированную
матрицу![]() ,
далее, все эле-менты транспонированной
матрицы заменить их алгебраическими
допол-нениями, а затем полученное
выражение разделить на определитель
,
далее, все эле-менты транспонированной
матрицы заменить их алгебраическими
допол-нениями, а затем полученное
выражение разделить на определитель![]()
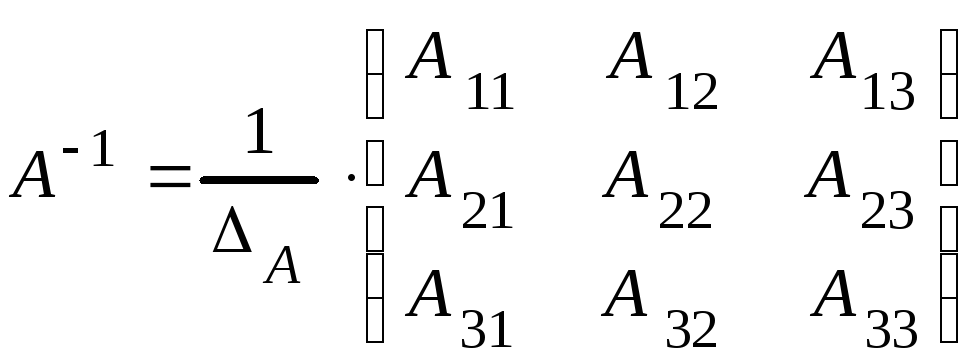 . (1.4)
. (1.4)
