
- •ВыСшая математика
- •Линейная, векторная алгебра
- •И аналитическая геометрия
- •Методические указания
- •3. Аналитическая геометрия на плоскости …………… 23
- •1. Линейная алгебра
- •1.1. Определители. Вычисление определителей
- •1.2. Матрицы и их свойства
- •1.3. Решение систем линейных уравнений
- •1.4. Решение типовых примеров задания 1 ргр
- •2. Векторная алгебра
- •2.1. Векторные и скалярные величины. Разложение вектора по координатным осям
- •2.2. Скалярное произведение двух векторов
- •. Условие параллельности и перпендикулярности векторов.
- •2.3.1. Решение типовых примеров задания 3 ргр
- •2.4. Смешанное произведение трех векторов
- •2.4.1. Решение типовых примеров задания 4 ргр
- •3. Аналитическая геометрия на плоскости
- •3.1. Длина и направление отрезка. Деление отрезка а заданном отношении. Площадь треугольника.
- •3.2. Прямая линия на плоскости
- •. Уравнение прямой с заданным угловым коэффициентом , (3.8)
- •. Уравнение прямой в отрезках на осях
- •Условие параллельности прямых
- •3.3. Кривые второго порядка в прямоугольной системе координат
- •3.3.1. Решение типовых примеров заданий 6, 7 ргр
- •3.4. Кривые второго порядка в полярной системе координат. Параметрические уравнения плоских кривых
- •Некоторые типы кривых на плоскости, заданных
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость . Основные уравнения плоскости
- •2. Направляющие косинусы нормали определяются по формулам
- •3. Условие параллельности плоскостей
- •4.1.1. Решение типовых примеров задания 8 ргр
- •4.2. Прямая линия в пространстве. Пересечение прямой и плоскости
- •4.2.1. Решение типовых примеров заданий 9, 10 ргр
- •Задания расчетно-графической работы №1 Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Формулы элементарной математикИ
- •7. Формулы двойного угла
- •8. Формулы понижения степени
- •9. Преобразование произведения тригонометрических функций в сумму
- •Приложение 4 Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Номера индивидуальных заданий Две последние цифры номера зачетной книжки
- •Расчетно-графическая работа
Задание 6
1. Привести к каноническому виду уравнение кривой. Найти координаты ее центра, радиус и построить кривую.
2. Составить уравнение геометрического
места точек, отношение расстояний
которых от точки
![]() к расстоянию до прямой
к расстоянию до прямой![]() равно числу
равно числу![]() .
Полученное уравнение привести к
каноническому виду. Найти полуоси
.
Полученное уравнение привести к
каноническому виду. Найти полуоси![]() и
и![]() ,
координаты фокусов
,
координаты фокусов![]()
![]() и построить кривую.
и построить кривую.
6.1. 1.
![]() .
2.
.
2.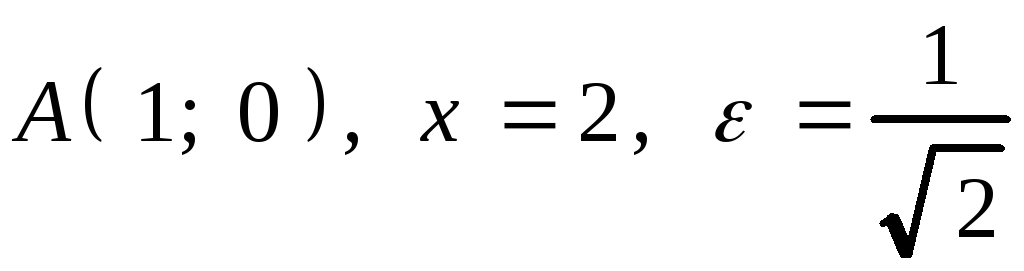 .
.
6.2. 1.
![]() . 2.
. 2. .
.
6.3. 1.
![]() . 2.
. 2.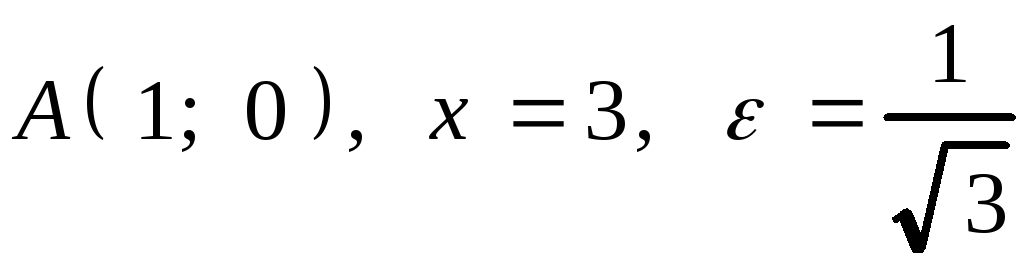 .
.
6.4. 1.
![]() . 2.
. 2.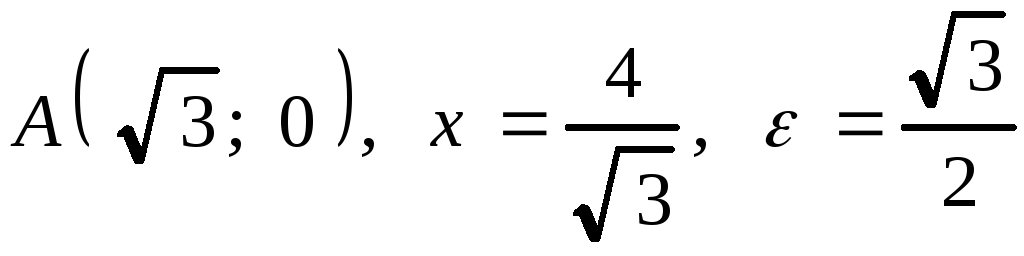 .
.
1.
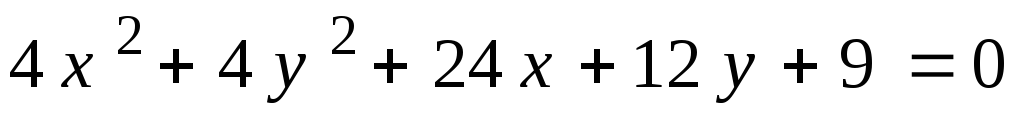 . 2.
. 2.
6.6. 1.
![]() . 2.
. 2. .
.
6.7. 1.![]() . 2.
. 2.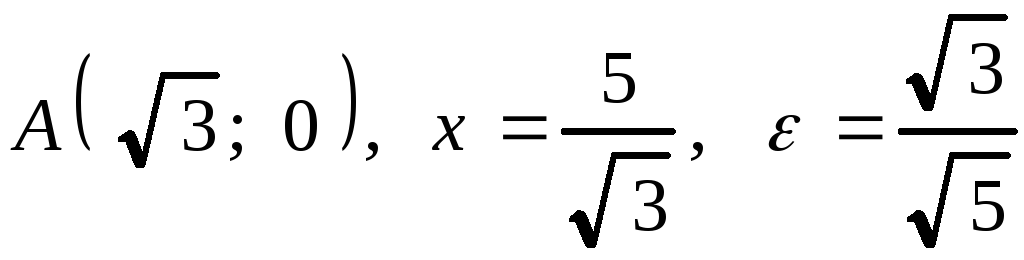 .
.
6.8. 1.
![]() . 2.
. 2.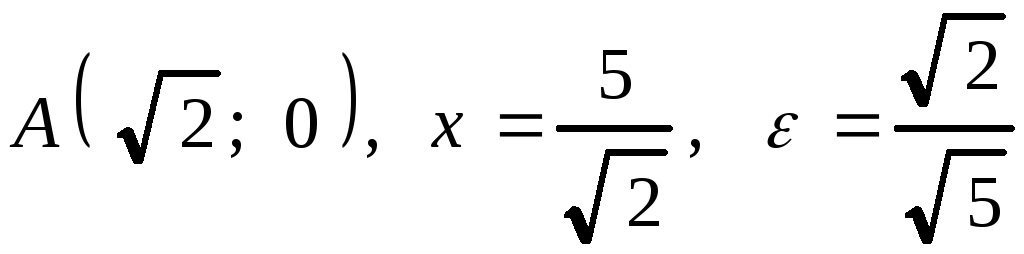 .
.
6.9. 1.
![]() . 2.
. 2.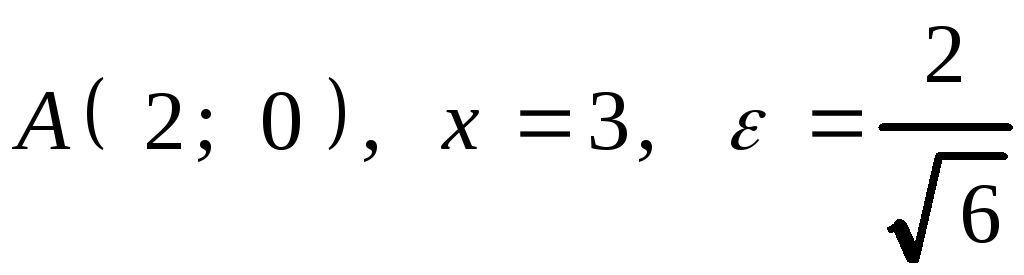 .
.
1.
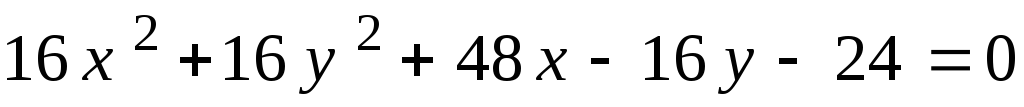 .
2.
.
2.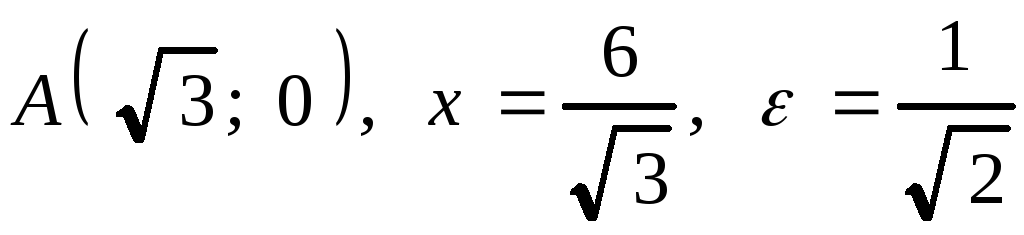 .
.
6.11. 1.
![]() .
2.
.
2.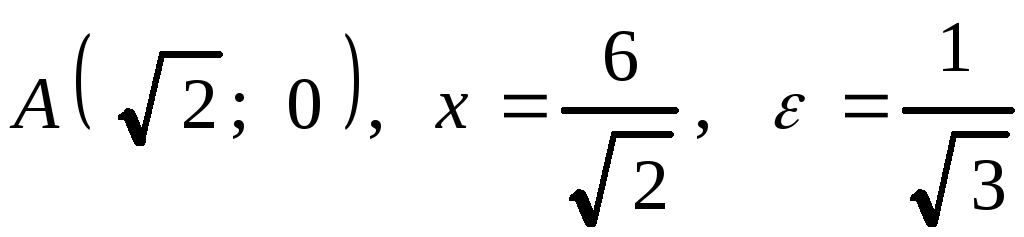 .
.
6.12. 1.
![]() .
2.
.
2.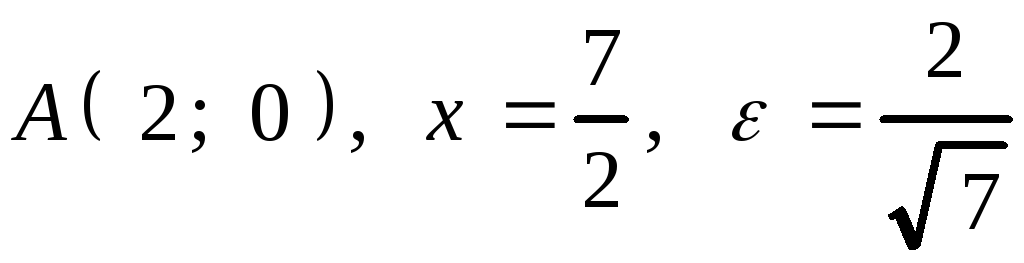 .
.
6.13. 1.
![]() .
2.
.
2.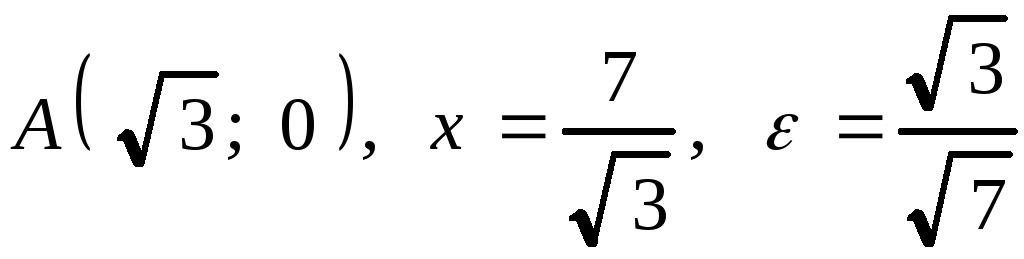 .
.
6.14. 1.
![]() .
2.
.
2.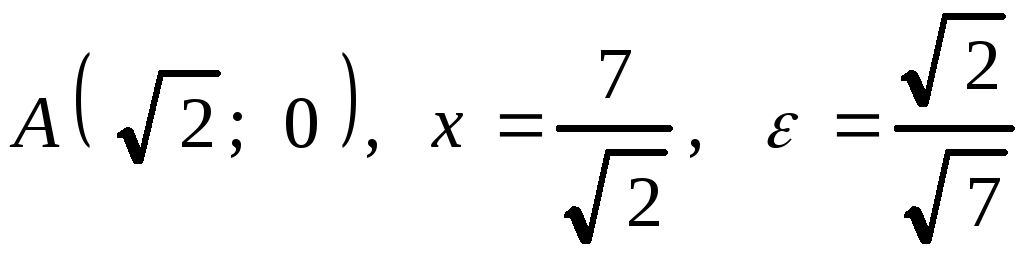 .
.
6.15. 1.
![]() .
2.
.
2. .
.
6.16. 1.
![]() .
2.
.
2.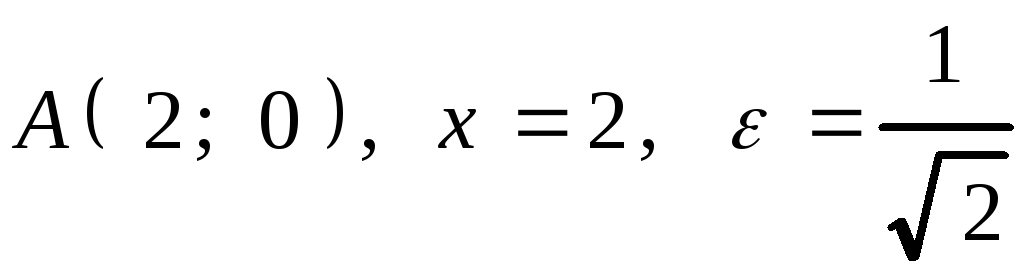 .
.
6.17. 1.
![]() .
2.
.
2.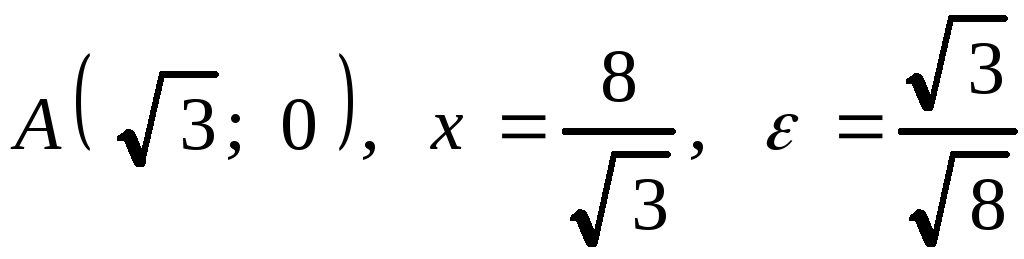 .
.
6.18. 1.
![]() .
2.
.
2.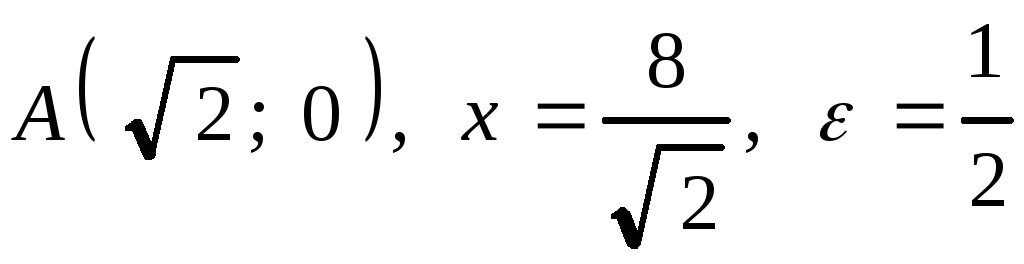 .
.
6.19. 1.
![]() .
2.
.
2.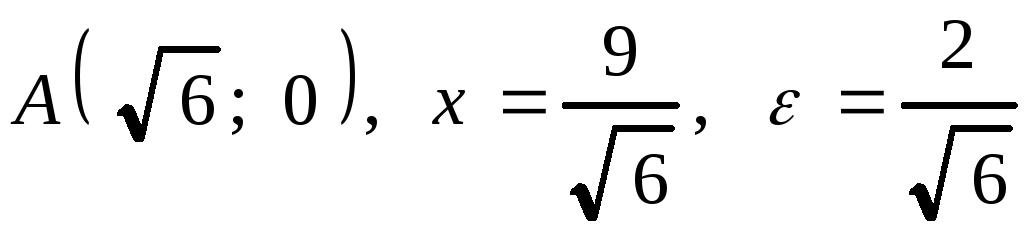 .
.
6.20. 1.
![]() .
2.
.
2.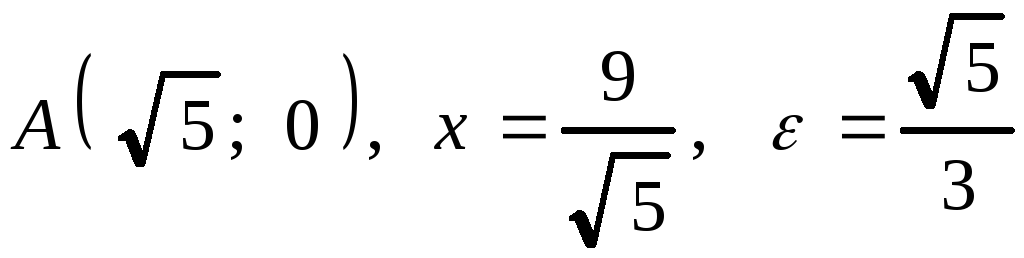 .
.
6.21. 1.
![]() .
2.
.
2.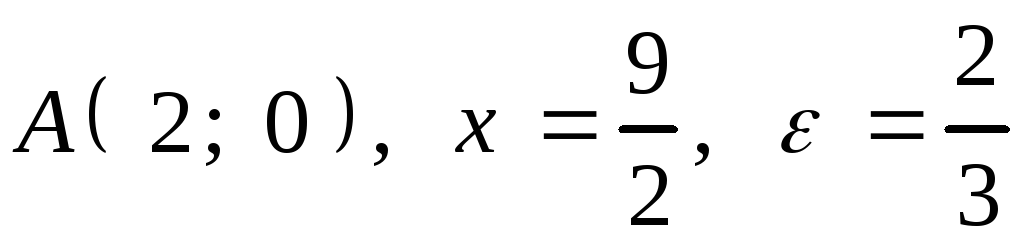 .
.
6.22. 1.
![]() .
2.
.
2.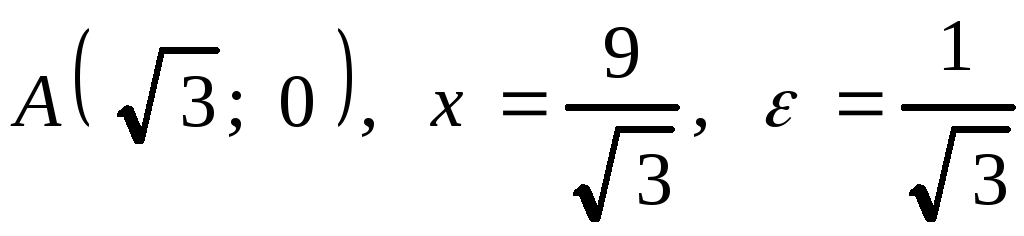 .
.
6.23. 1.
![]() .
2.
.
2.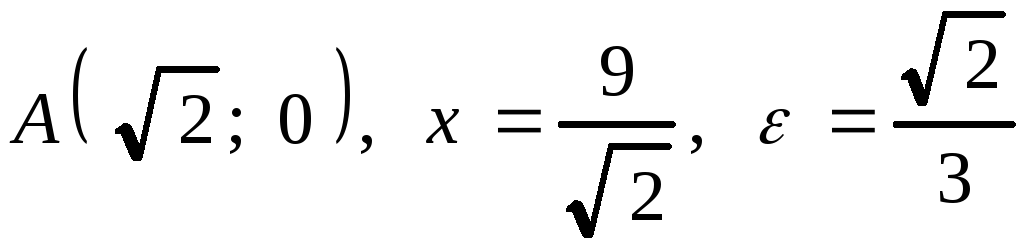 .
.
6.24. 1.
![]() .
2.
.
2.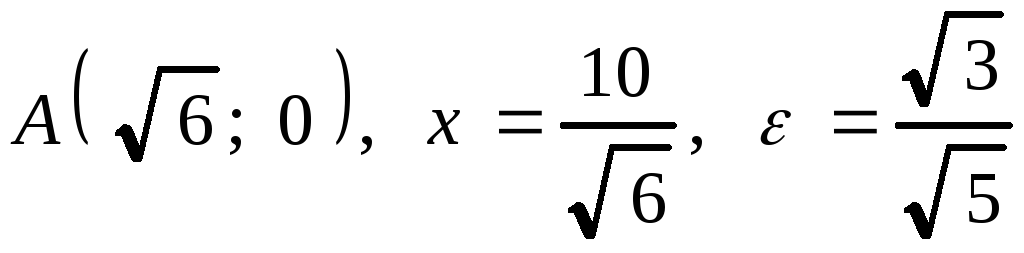 .
.
6.25. 1.
![]() .
2.
.
2.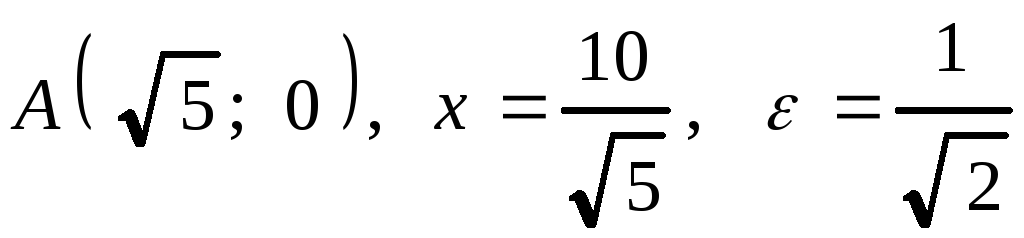 .
.
6.26. 1.
![]() .
2.
.
2.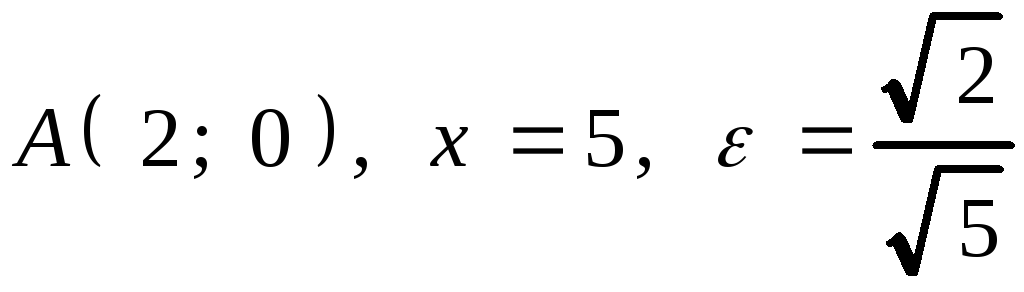 .
.
6.27. 1.
![]() .
2.
.
2.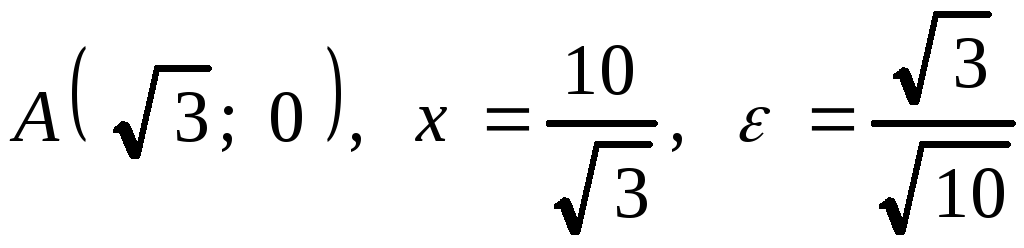 .
.
6.28. 1.
![]() .
2.
.
2. .
.
6.29. 1.
![]() .
2.
.
2.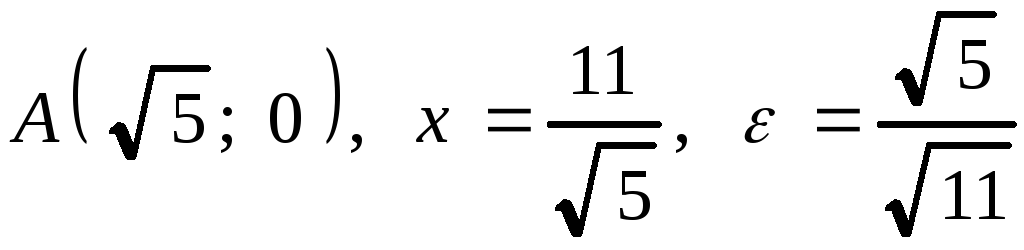 .
.
6.30. 1.
![]() .
2.
.
2. .
.
Задание 7
1. Составить каноническое уравнение
геометрического места точек, отношение
расстояний которых от точки
![]() к расстоянию до прямой
к расстоянию до прямой![]() равно
равно![]() .
Найти координаты фокусов
.
Найти координаты фокусов![]() ,
вершин
,
вершин![]() ,
эксцентриситет
,
эксцентриситет![]() ,
и уравнения асимптот кривой. Определить
координаты точек
,
и уравнения асимптот кривой. Определить
координаты точек![]() пересечения кривой с окружностью, центр
которой находится в начале координат,
а окружность проходит через ее фокусы.
Построить асимптоты, кривую и окружность.
пересечения кривой с окружностью, центр
которой находится в начале координат,
а окружность проходит через ее фокусы.
Построить асимптоты, кривую и окружность.
2. Привести уравнение кривой к каноническому
виду. Найти параметр
![]() кривой, координаты вершины
кривой, координаты вершины![]() ,
фокуса
,
фокуса![]() и уравнение директрисы. Построить
кривую и ее директрису.
и уравнение директрисы. Построить
кривую и ее директрису.
7.1. 1.
![]() 2.
2.![]() .
.
7.2. 1.
![]() 2.
2.![]() .
.
7.3. 1.
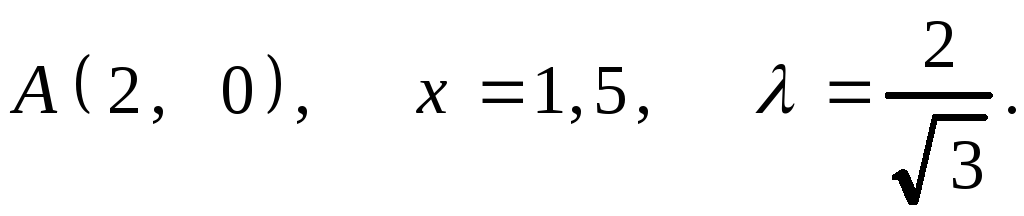 2.
2.![]()
1.
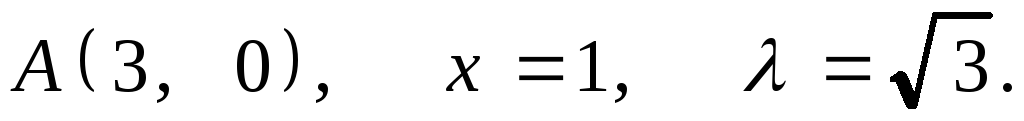 2.
2.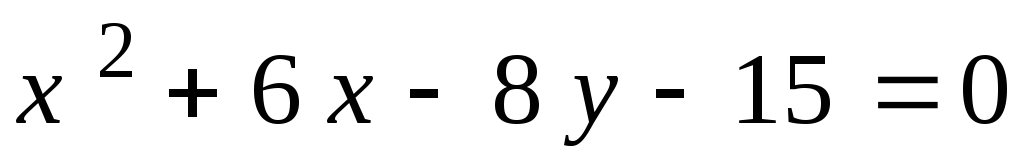 .
.1.
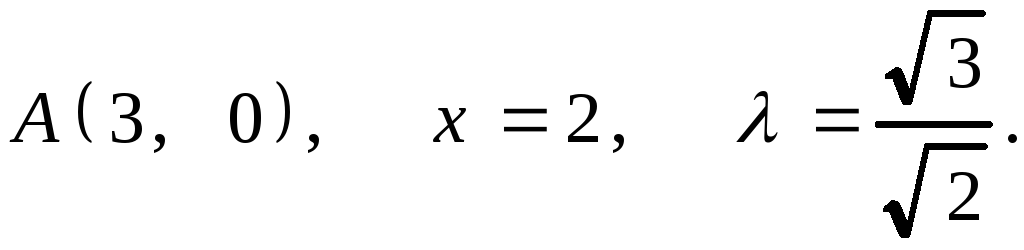 2.
2.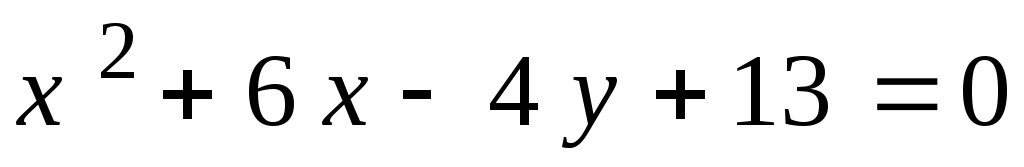 .
.1.
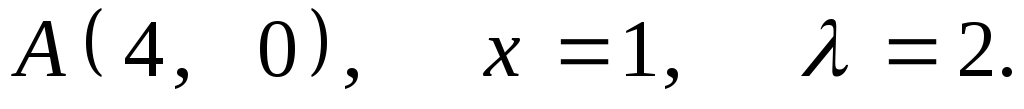 2.
2.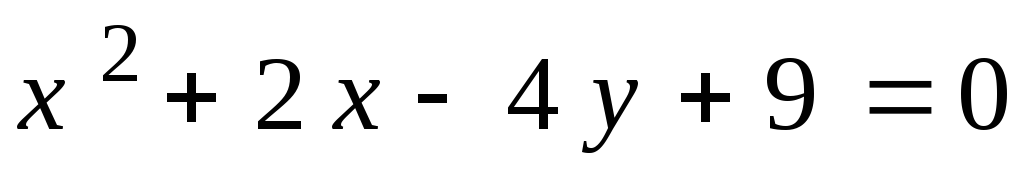 .
.1.
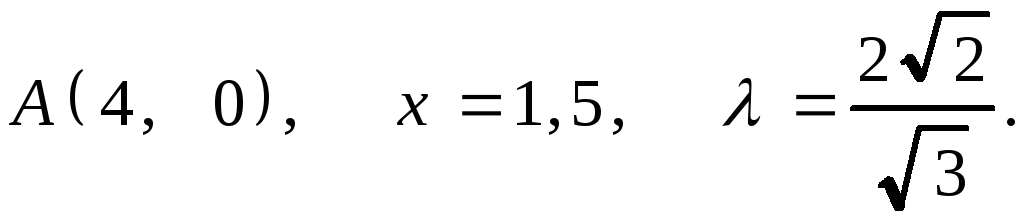 2.
2.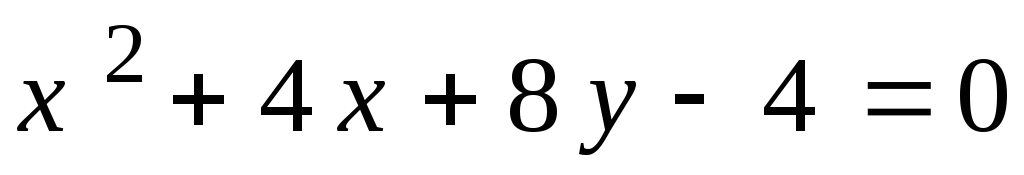 .
.1.
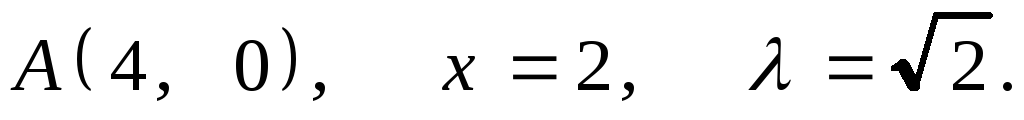 2.
2. .
.1.
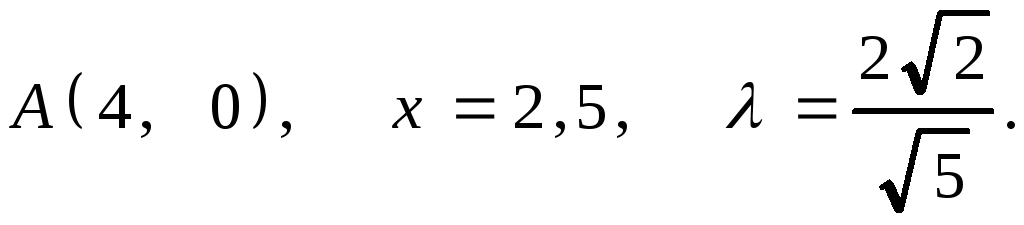 2.
2.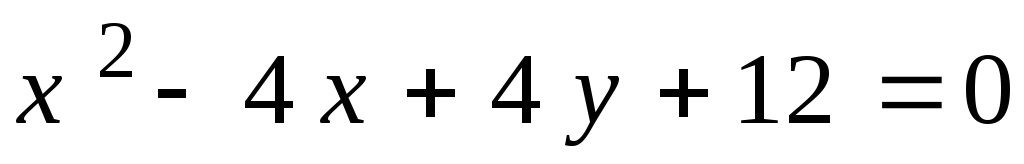 .
.
7.10. 1.
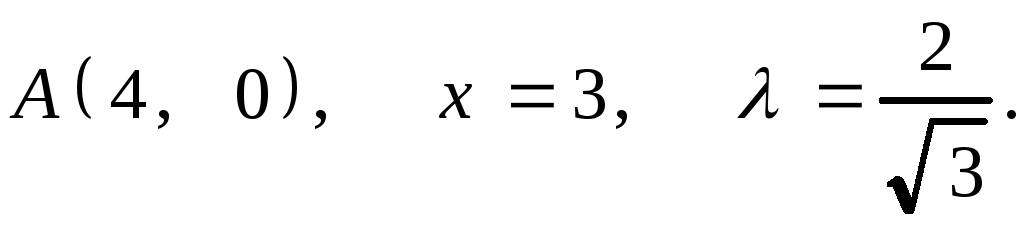 2.
2.![]() .
.
7.11. 1.
![]() 2.
2.![]() .
.
7.12. 1.
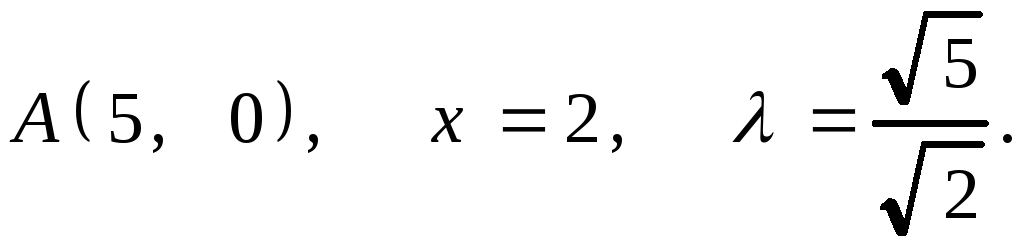 2.
2.![]() .
.
1.
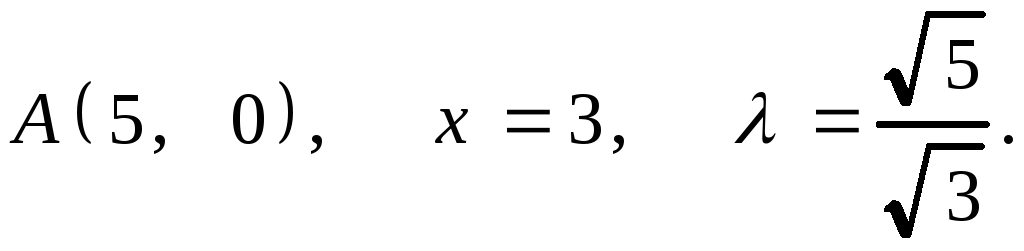 2.
2.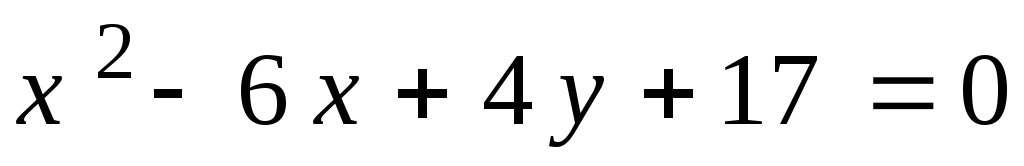 .
.
7.14. 1.
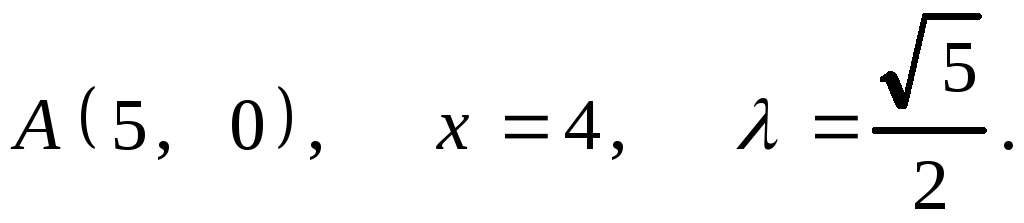 2.
2.![]() .
.
7.15. 1.
![]() 2.
2.![]() .
.
7.16. 1.
![]() 2.
2.![]() .
.
7.17. 1.
![]() 2.
2.![]() .
.
7.18. 1.
![]() 2.
2.![]() .
.
7.19. 1.
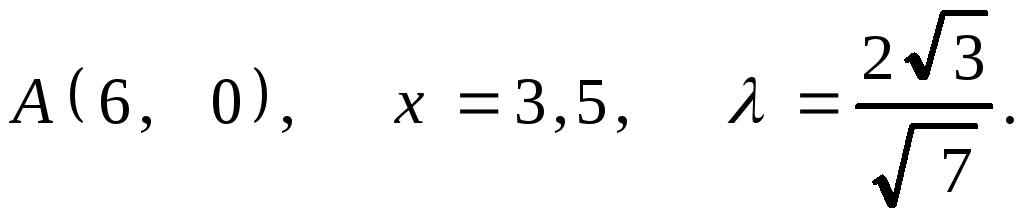 2.
2.![]() .
.
7.20. 1.
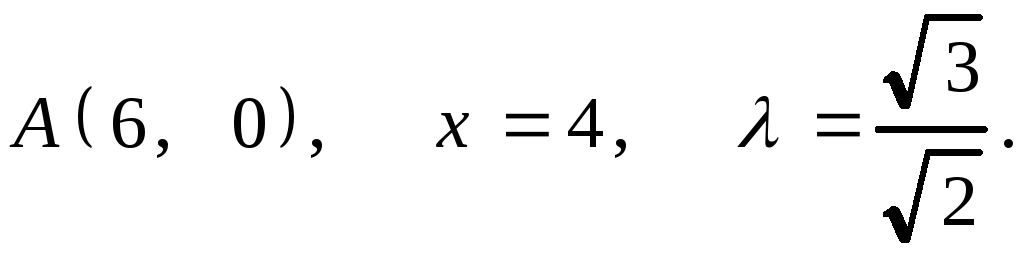 2.
2.![]() .
.
7.21. 1.
![]() 2.
2.![]() .
.
7.22. 1.
![]() 2.
2.![]() .
.
7.23. 1.
 2.
2.![]() .
.
7.24. 1.
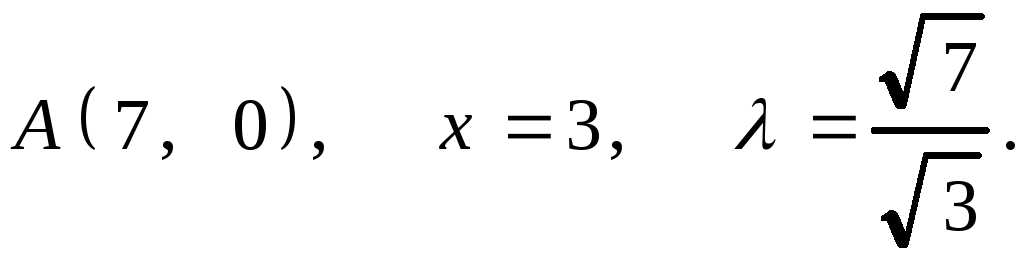 2.
2.![]() .
.
7.25. 1.
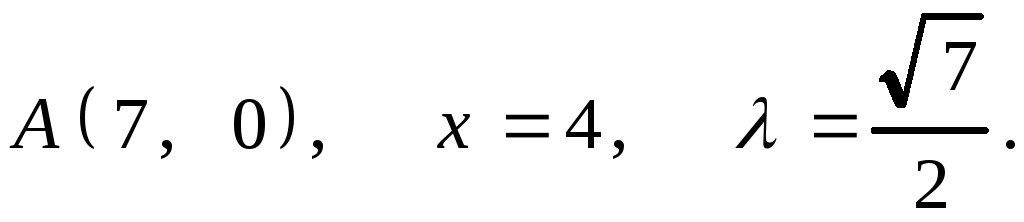 2.
2.![]() .
.
7.26. 1.
![]() 2.
2.![]() .
.
7.27. 1.
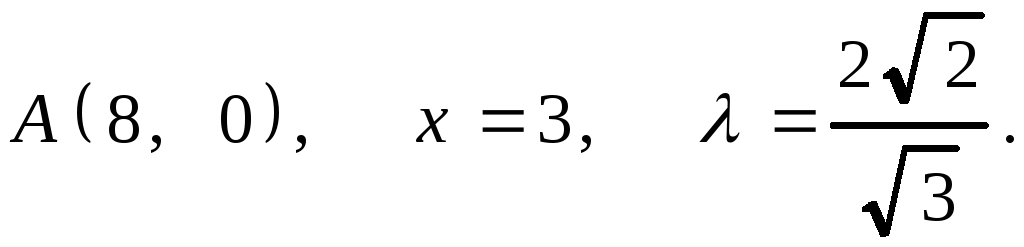 2.
2.![]() .
.
7.28. 1.
![]() 2.
2.![]() .
.
7.29. 1.
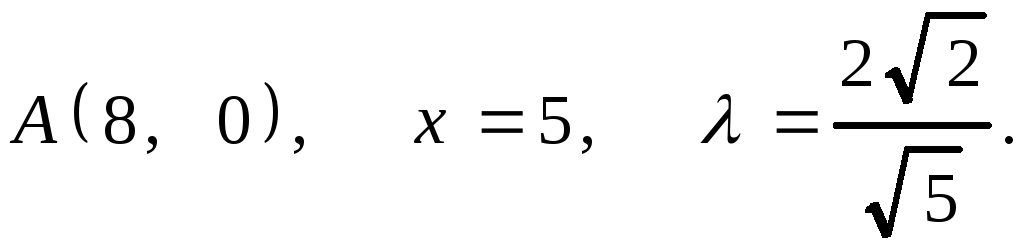 2.
2.![]() .
.
7.30. 1.
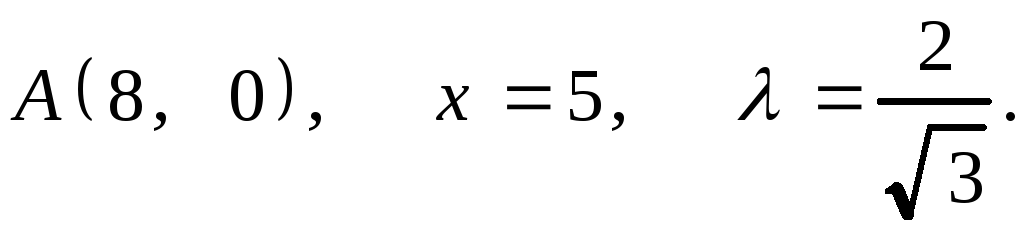 2.
2.![]() .
.
Задание 8
Даны координаты точек
![]() ,
,![]() ,
,![]() ,
,![]() .
Требуется:
.
Требуется:
1.
Написать уравнение плоскости: а)
![]() – проходящей через точку
– проходящей через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() ;б)
;б)
![]() – проходящей через точку
– проходящей через точку![]() параллельно векторам
параллельно векторам![]() и
и![]() в)проходящей
через точки
в)проходящей
через точки![]() .
.
2. Проверить,
выполняется ли условие перпендикулярности
плоскостей![]() ,
,![]() и параллельности плоскостей
и параллельности плоскостей![]() ,
,![]() .
.
3. Найти расстояние
![]() от точки
от точки![]() до плоскости
до плоскости![]() .
.
8.1.
![]()
![]()
![]()
![]()
8.2.
![]()
![]()
![]()
![]()
8.3.
![]()
![]()
![]()
![]()
8.6.
![]()
![]()
![]()
![]()
8.21.![]()
![]()
![]()
![]()
8.22.![]()
![]()
![]()
![]()
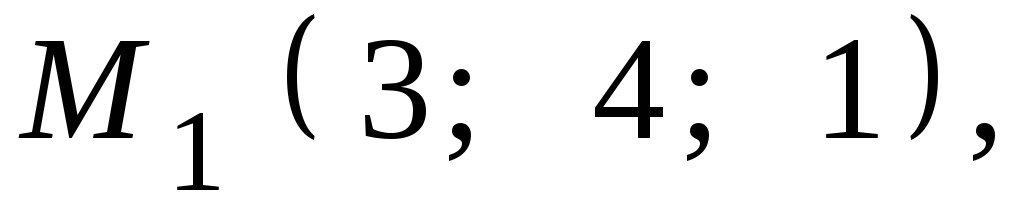
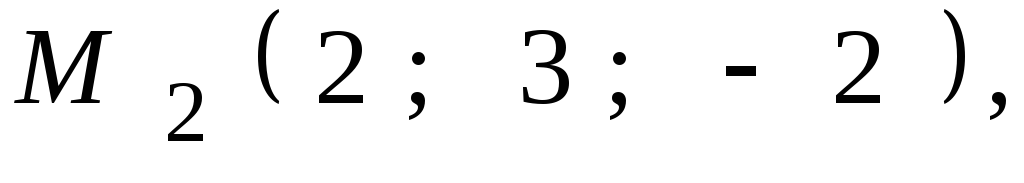
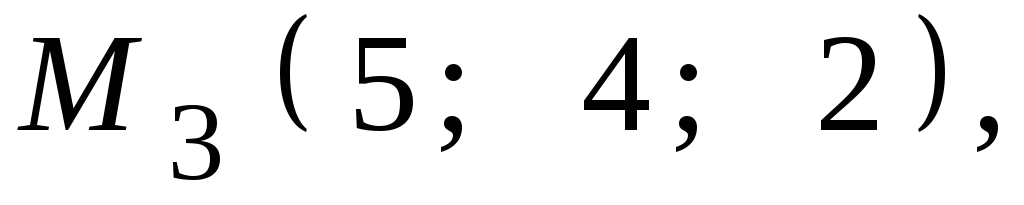
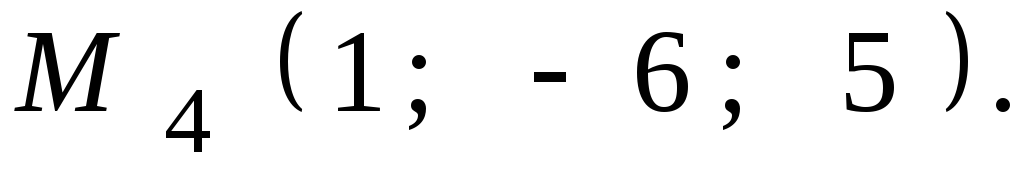

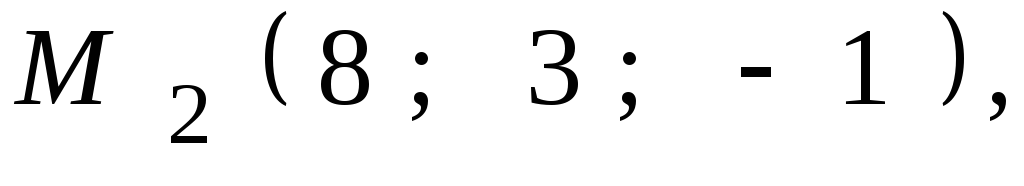
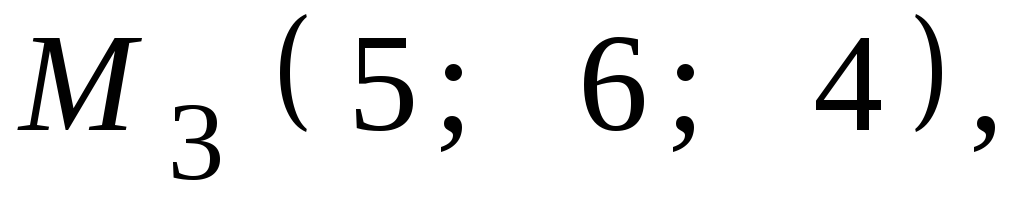

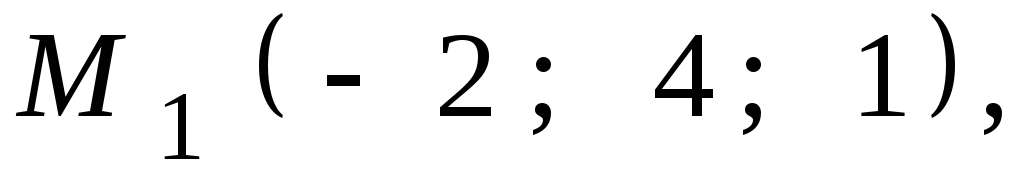
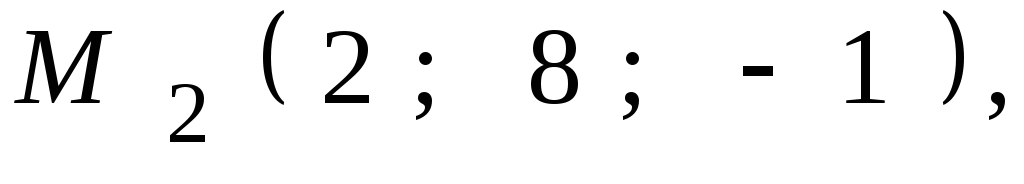
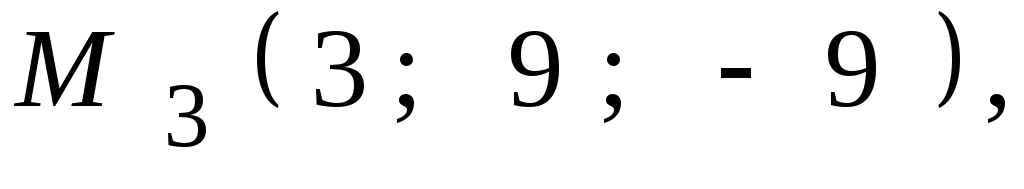
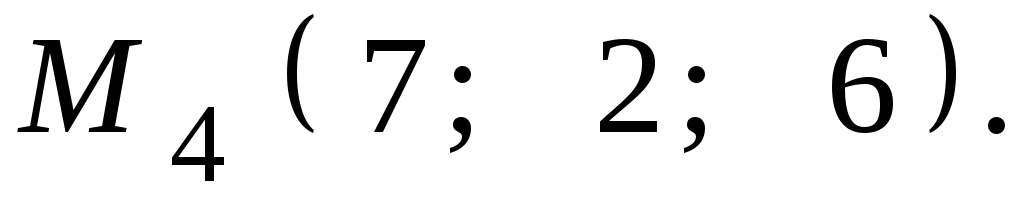
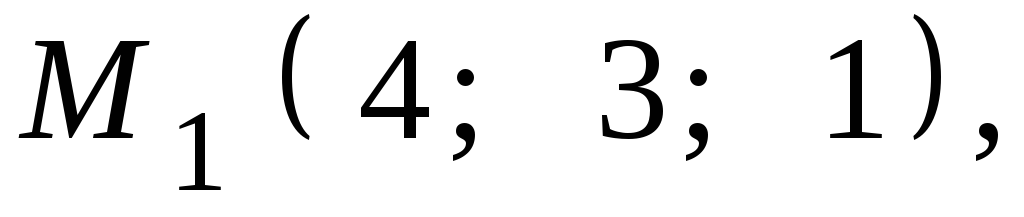
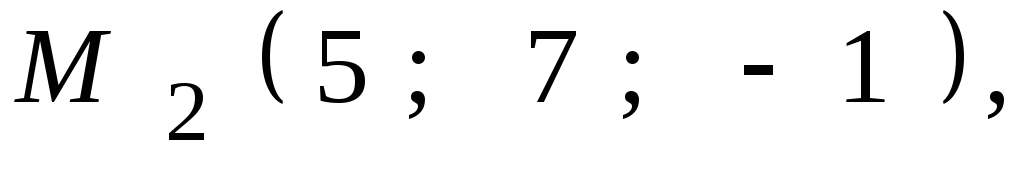

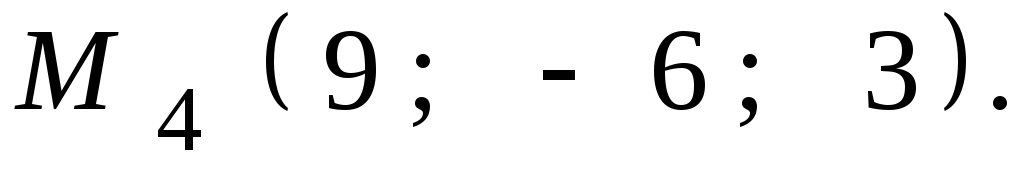
 ,
,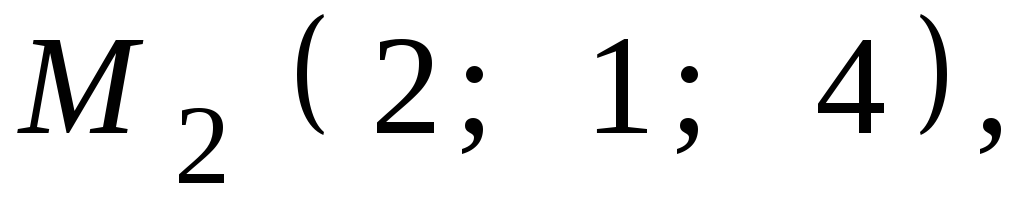
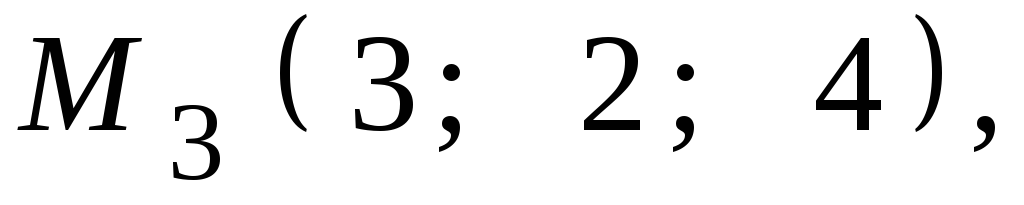

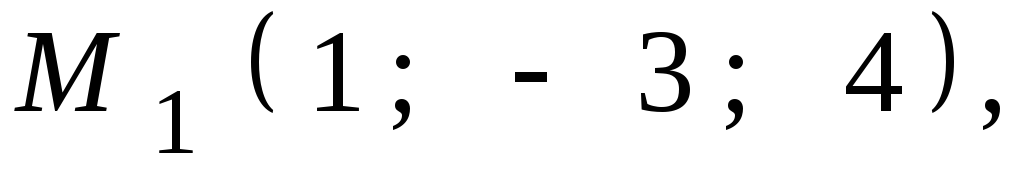
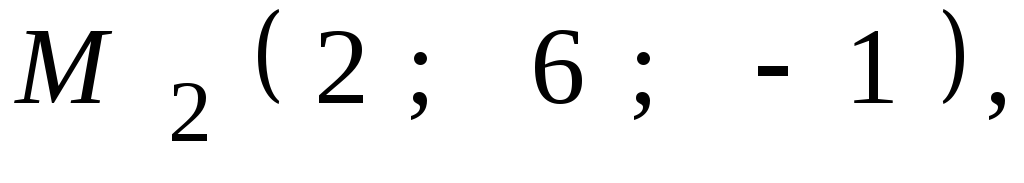
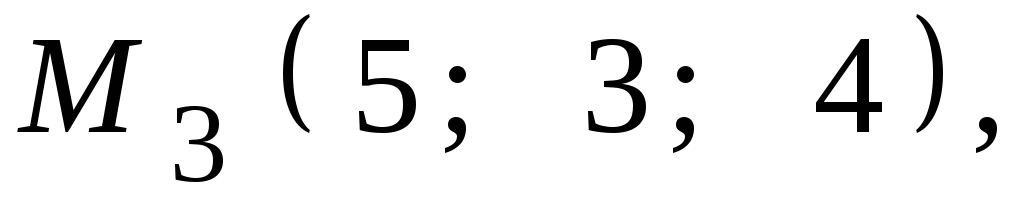
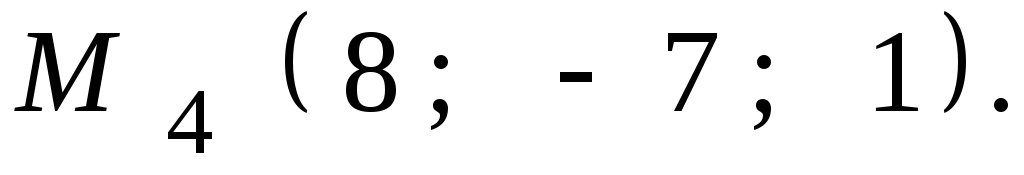
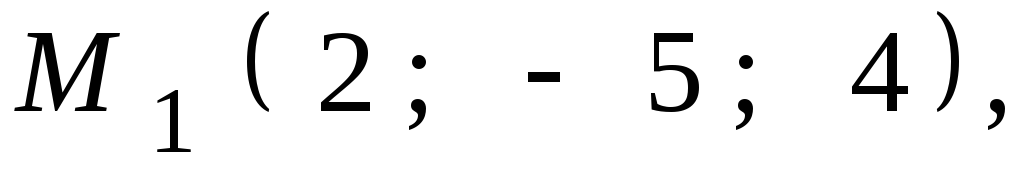

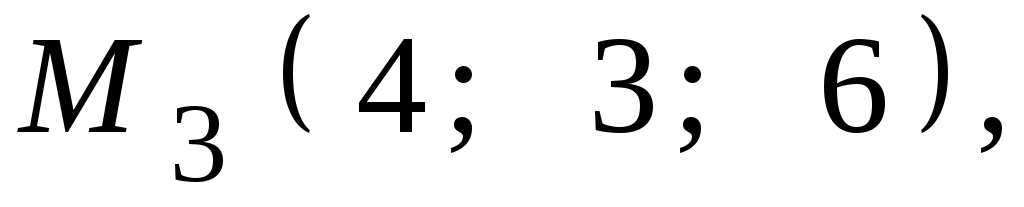
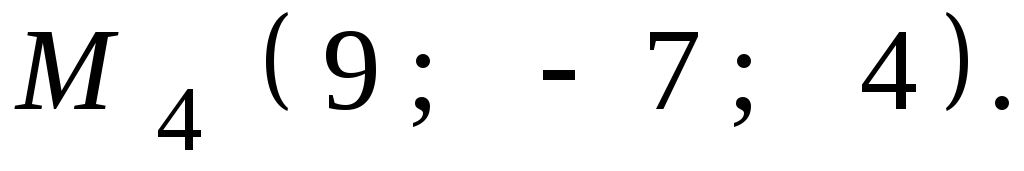
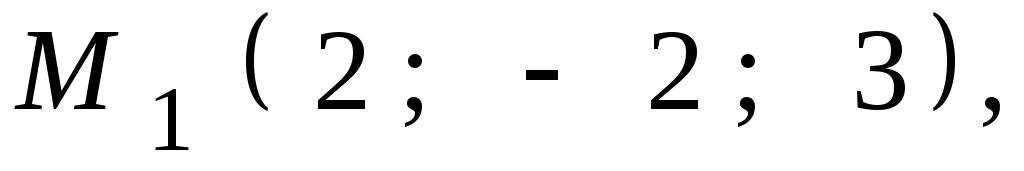
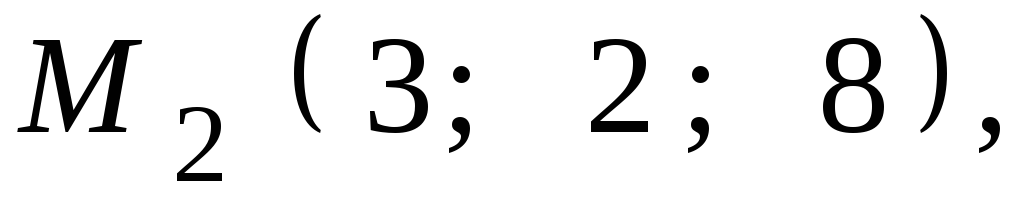
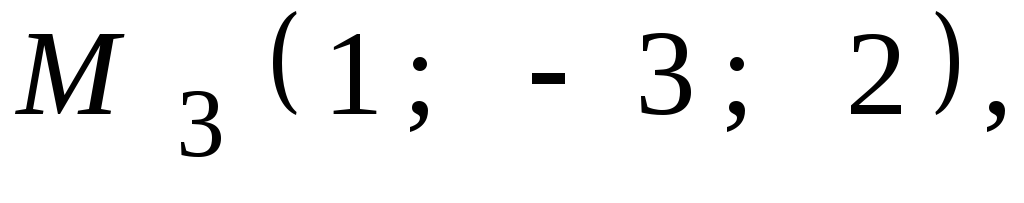
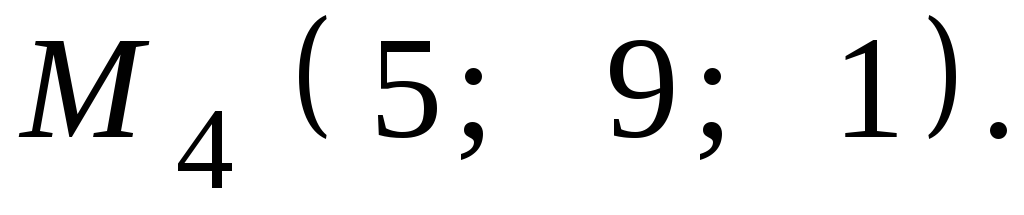
Задание 9
Задана прямая общими уравнениями и координаты двух точек. Необходимо: 1) написать канонические уравнения прямых; 2) найти угол между прямыми.
9.1.
![]() 9.2.
9.2.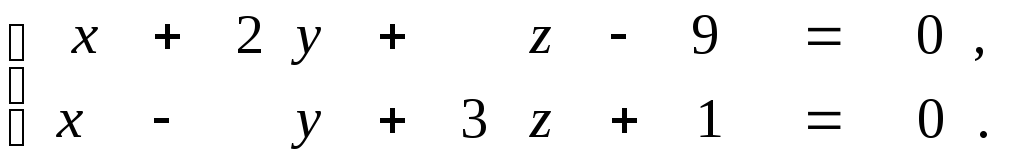
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.3.
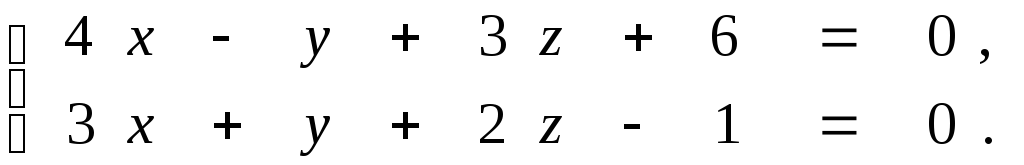 9.4.
9.4. ![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.5.
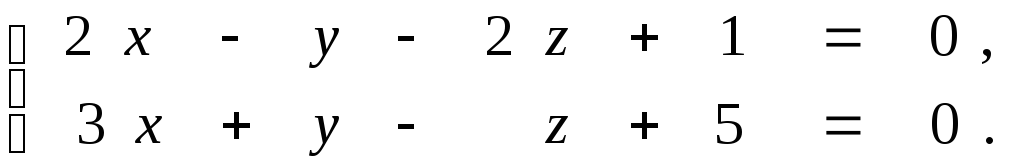 9.6.
9.6.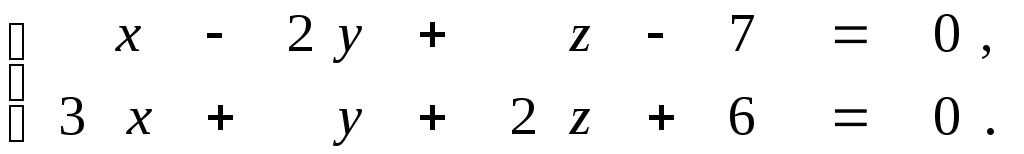
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.7.
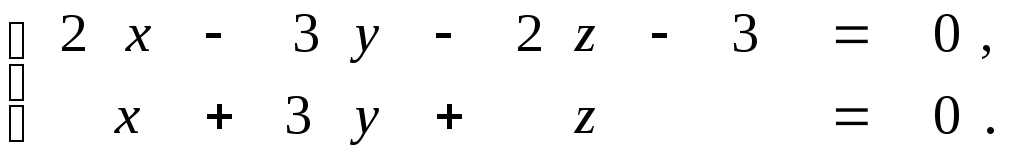 9.8.
9.8.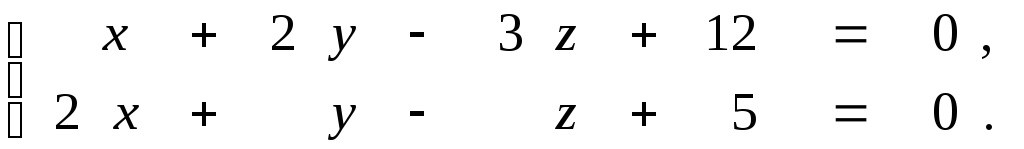
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.9.
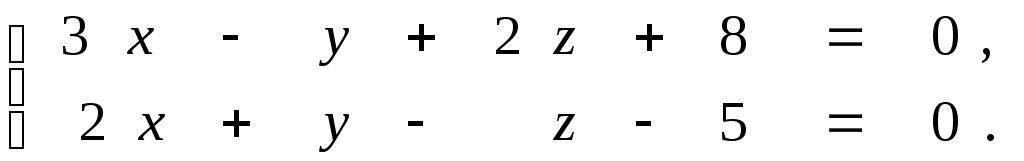 9.10.
9.10.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.11.
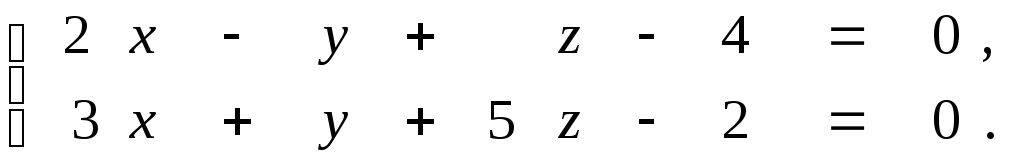 9.12.
9.12.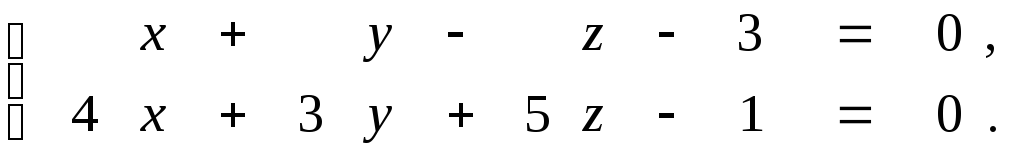
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.13.
![]() 9.14.
9.14.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.15.
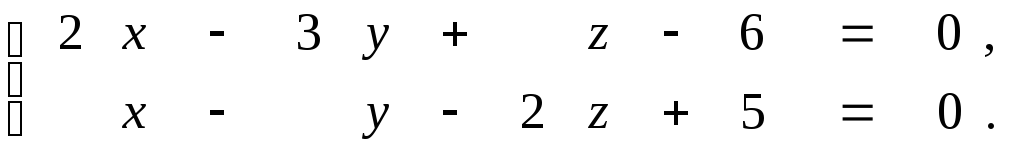 9.16.
9.16.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.17.
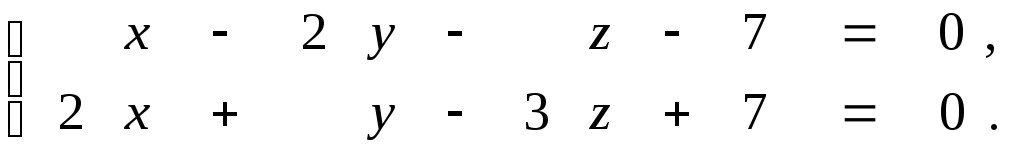 9.18.
9.18.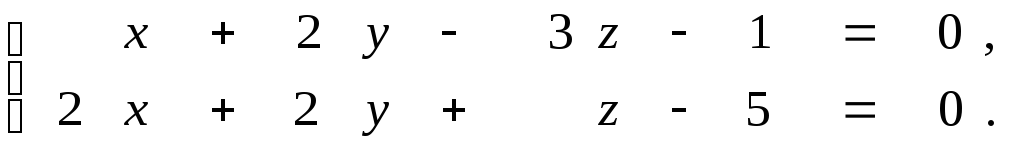
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.19.
![]() 9.20.
9.20.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.21.
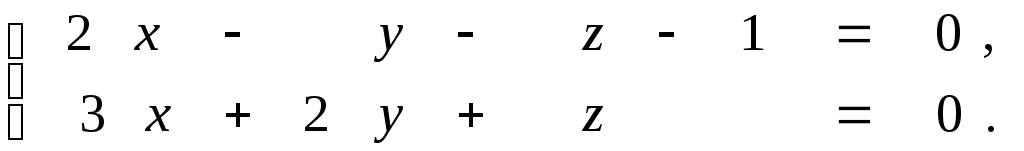 9.22.
9.22.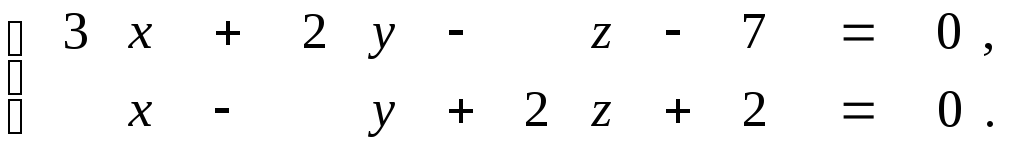
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.23.
![]() 9.24.
9.24.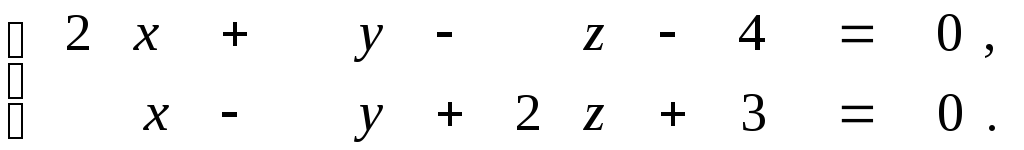
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.25.
![]() 9.26.
9.26.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.27.
![]() 9.28.
9.28.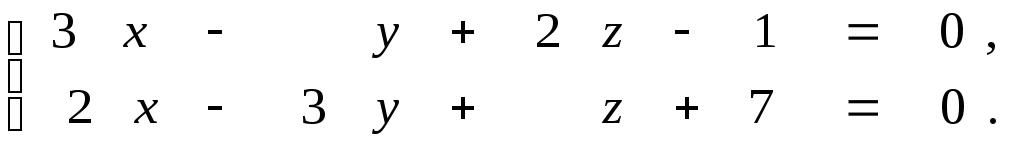
![]() ,
,![]() .
.![]() ,
,![]() .
.
9.29.
![]() 9.30.
9.30.![]()
![]() ,
,![]() .
.![]() ,
,![]() .
.
Задание 10
Даны прямая в пространстве и плоскость. Найти: а) точку пересече-ния прямой и плоскости;б) угол между прямой и плоскостью.
10.1.
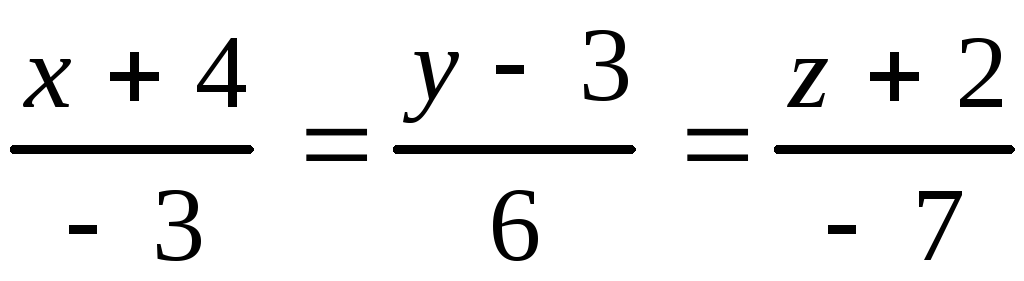 , 10.2.
, 10.2.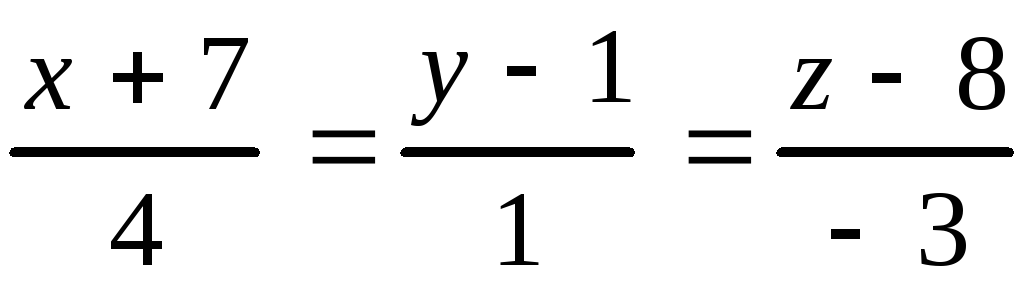 ,
,
![]() .
.![]() .
.
10.3.
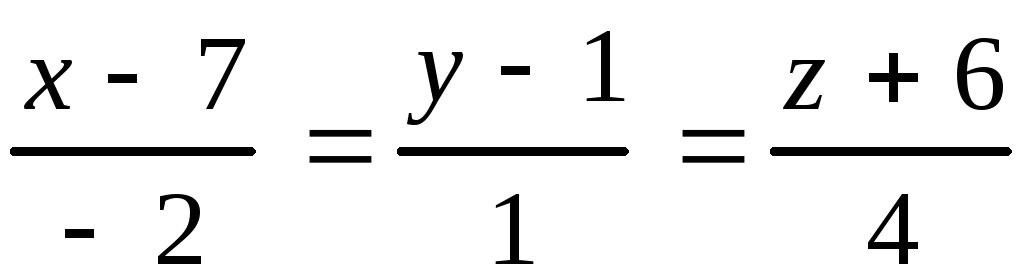 ,
10.4.
,
10.4.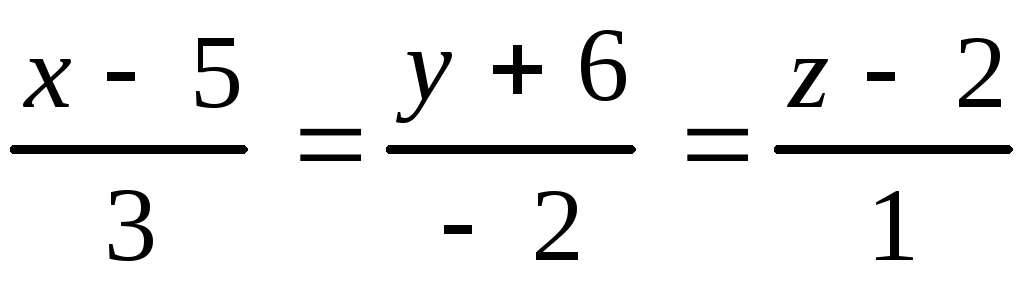 ,
,
![]() .
.![]() .
.
10.5.
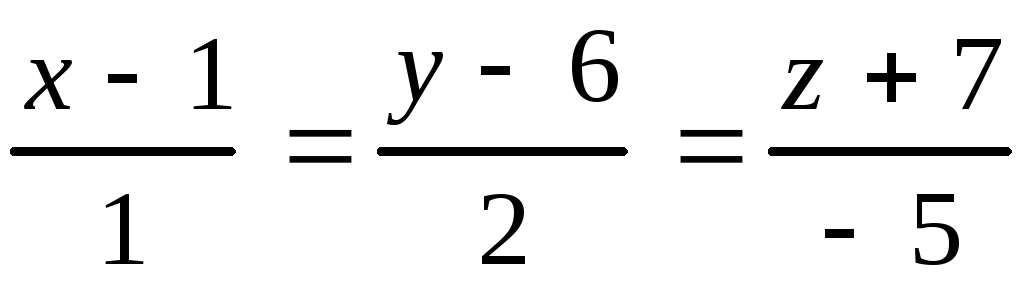 ,
10.6.
,
10.6.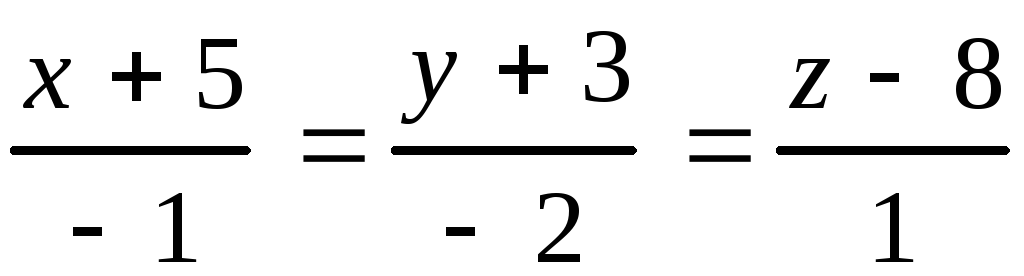 ,
,
![]() .
.![]() .
.
10.7.
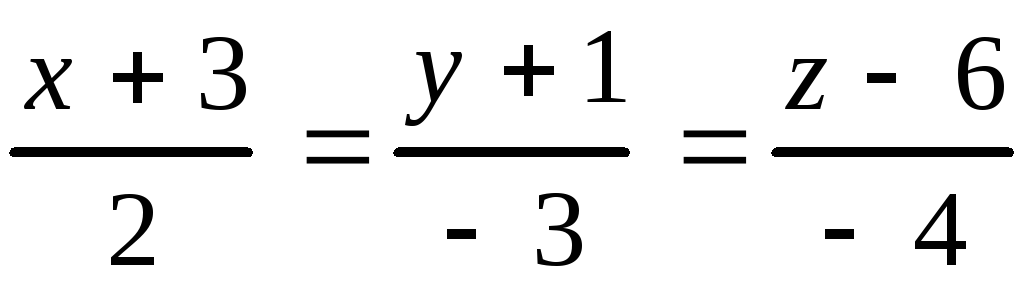 , 10.8.
, 10.8.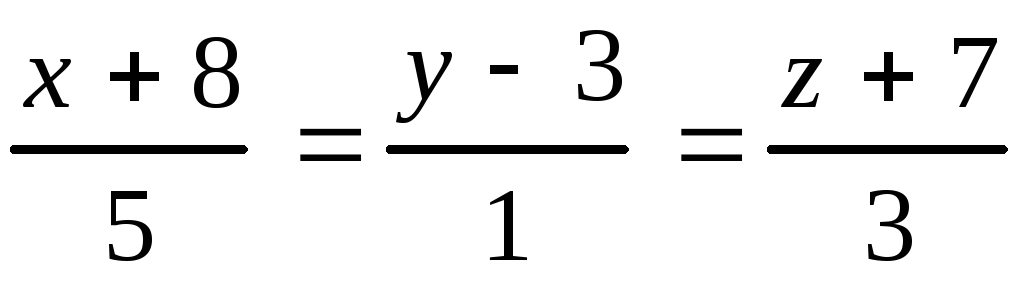 ,
,
![]() .
.![]() .
.
10.9.
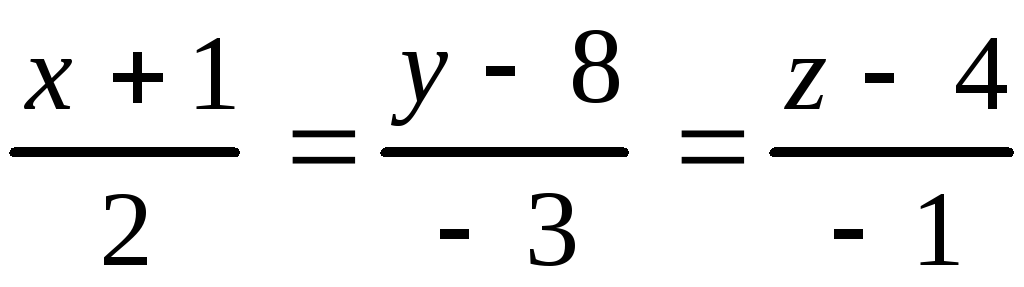 , 10.10.
, 10.10.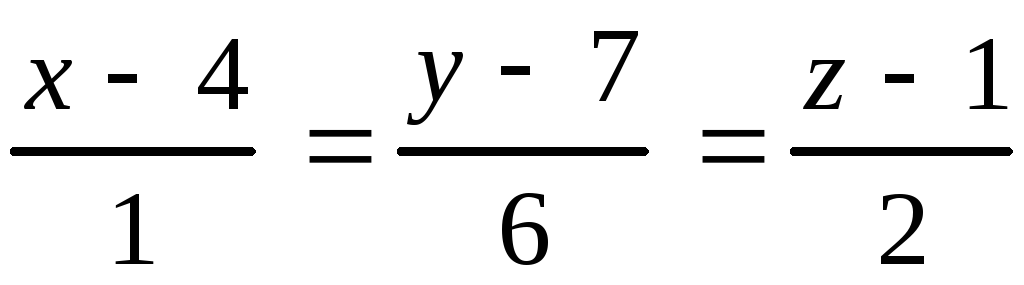 ,
,
![]() .
.![]() .
.
10.11.
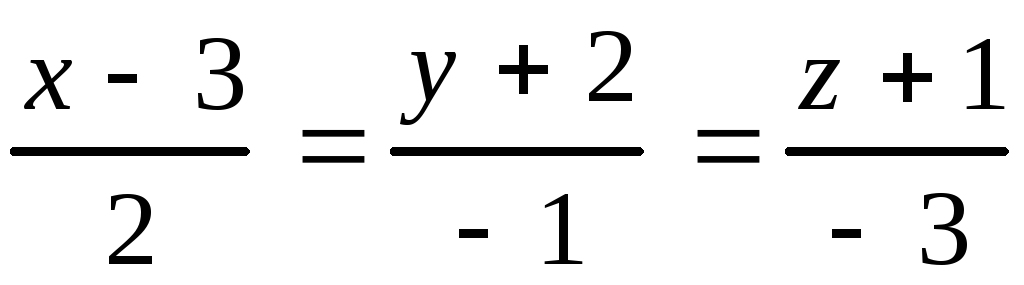 , 10.12.
, 10.12.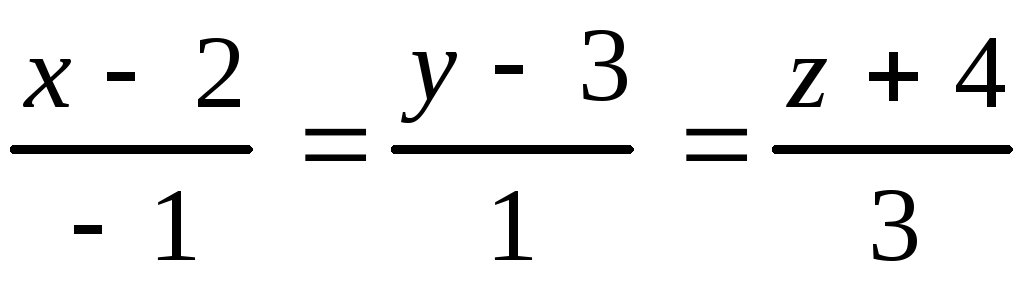 ,
,
![]() .
.![]() .
.
10.13.
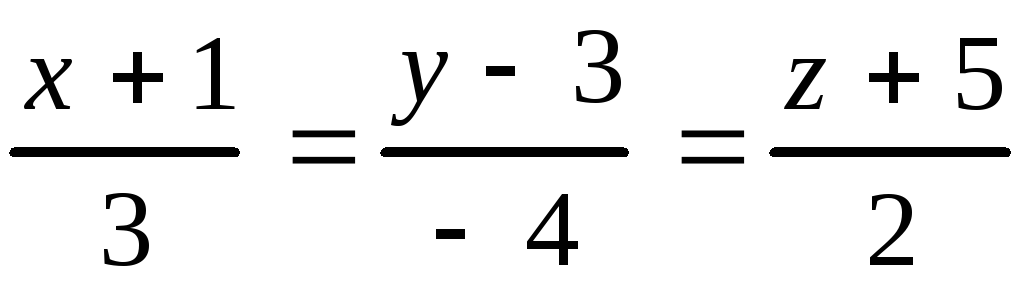 , 10.14.
, 10.14.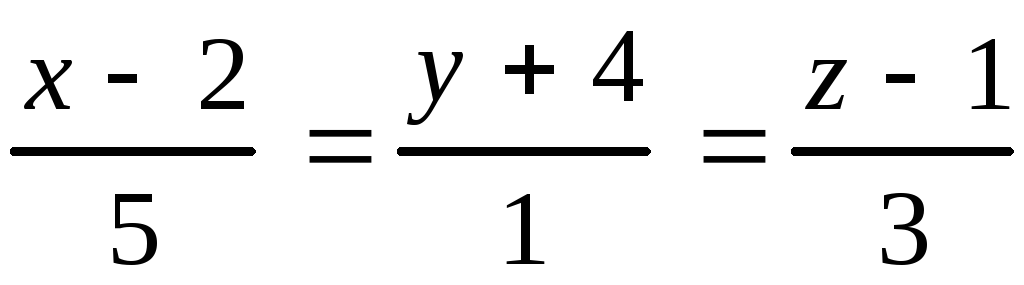 ,
,
![]() .
.![]() .
.
10.15.
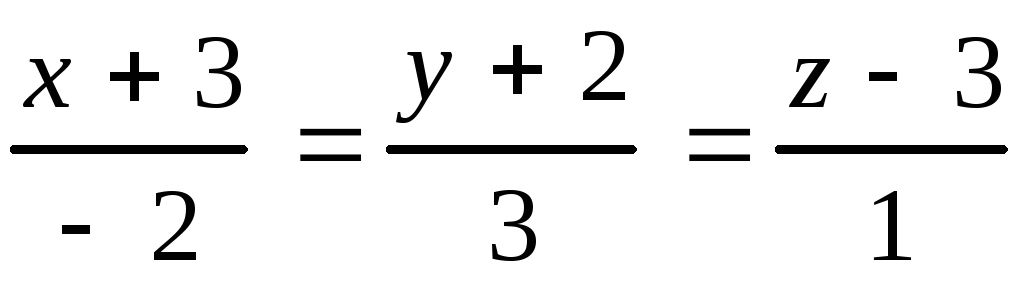 , 10.16.
, 10.16.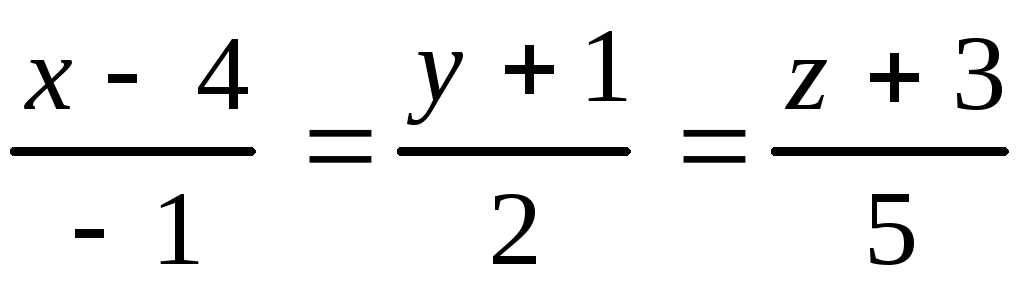 ,
,
![]() .
.![]() .
.
10.17.
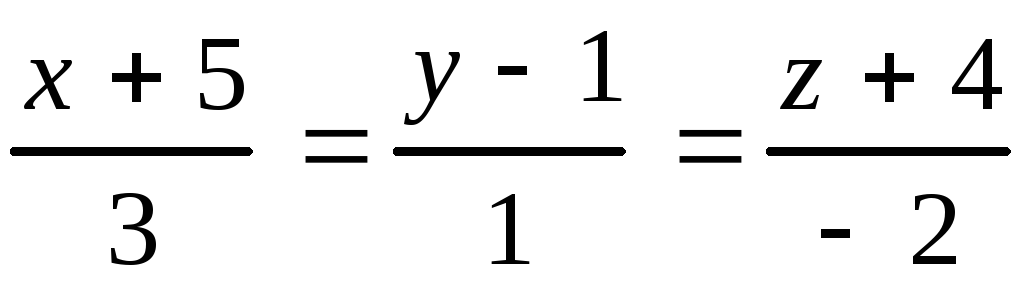 , 10.18.
, 10.18. ,
,
![]() .
.![]() .
.
10.19.
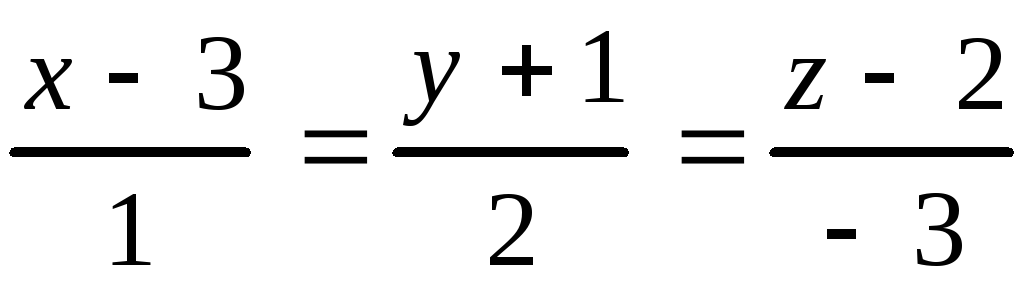 , 10.20.
, 10.20.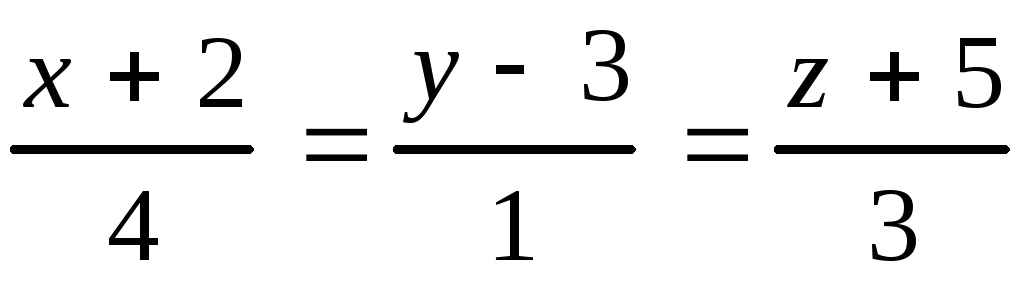 ,
,
![]() .
.![]() .
.
10.21.
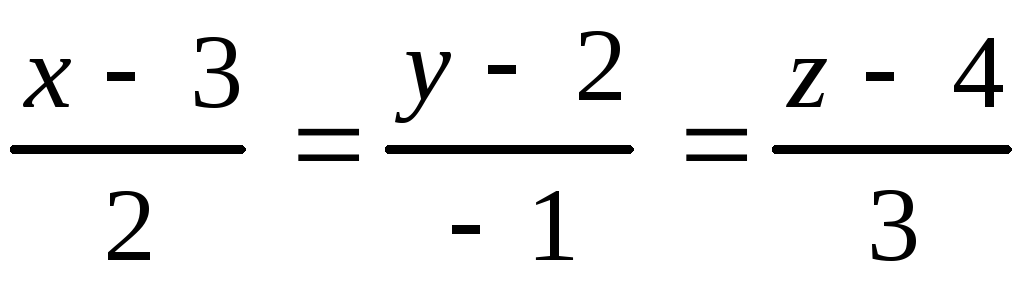 , 10.22.
, 10.22. ,
,
![]() .
.![]() .
.
10.23.
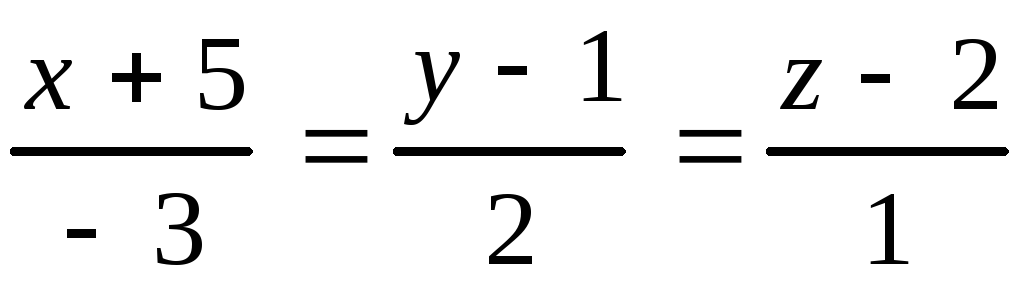 , 10.24.
, 10.24.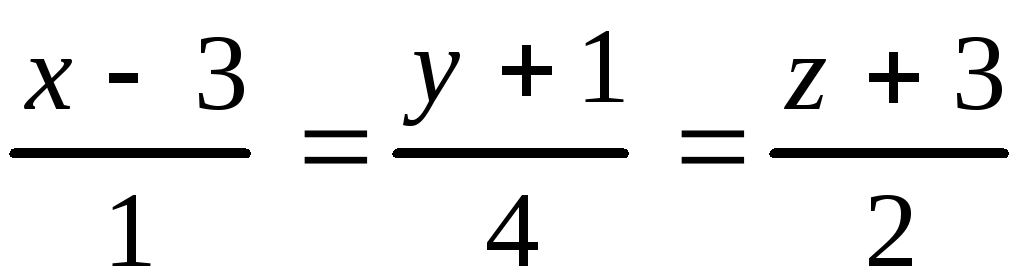 ,
,
![]() .
.![]() .
.
10.25.
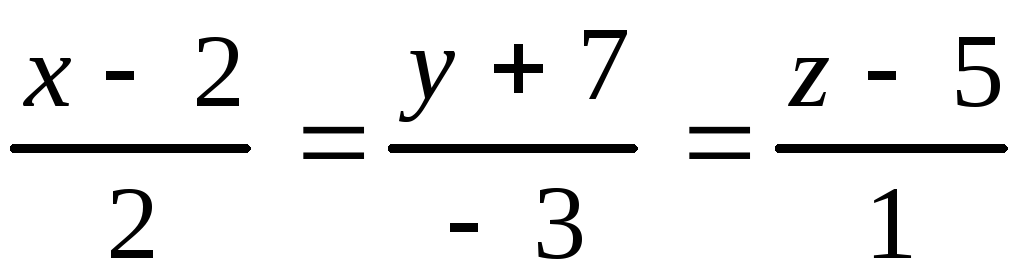 , 10.26.
, 10.26.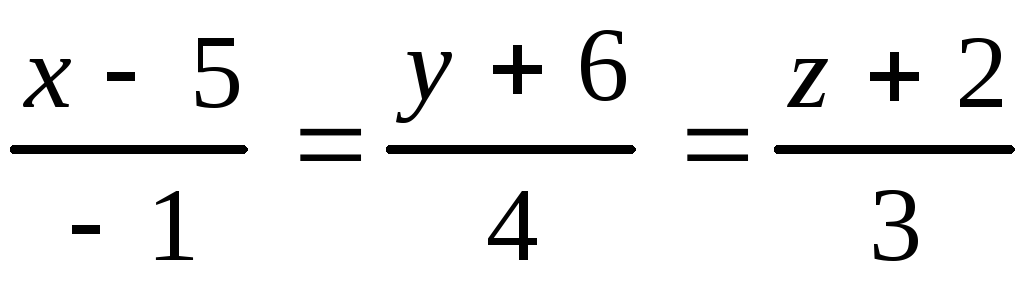 ,
,
![]() .
.![]() .
.
10.27.
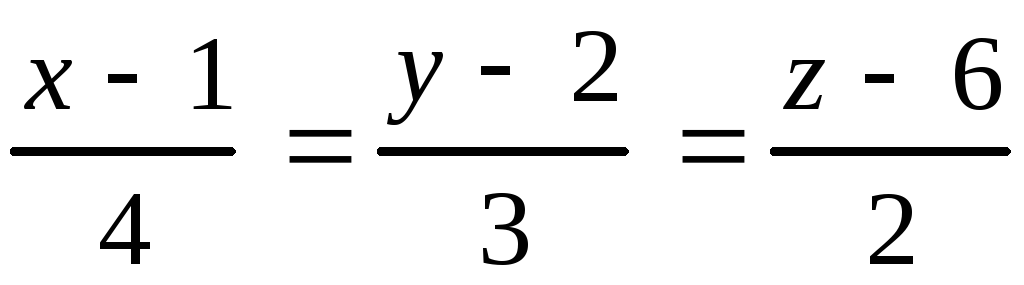 , 10.28.
, 10.28.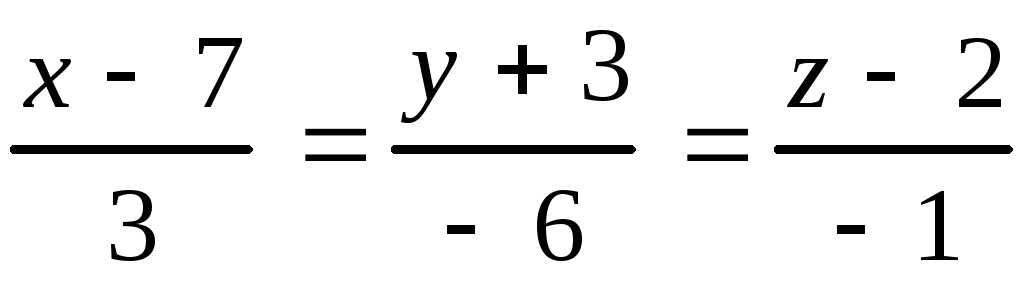 ,
,
![]() .
.![]() .
.
10.29.
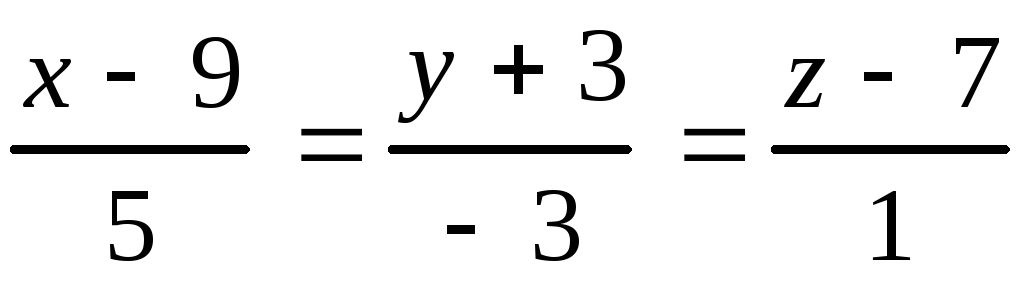 , 10.30.
, 10.30.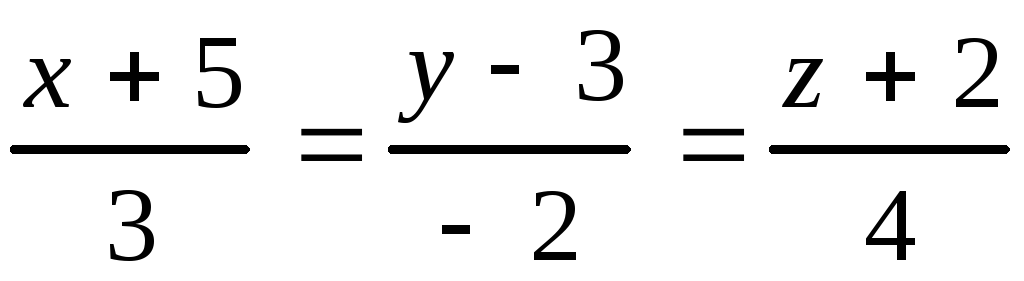 ,
,
![]() .
.![]() .
.
Приложение 1
