4.2. Прямая линия в пространстве. Пересечение прямой и плоскости

.Основные уравнения прямой линии

1. Прямая линия в пространствев общем видезадается пересечением двух плоскостей:

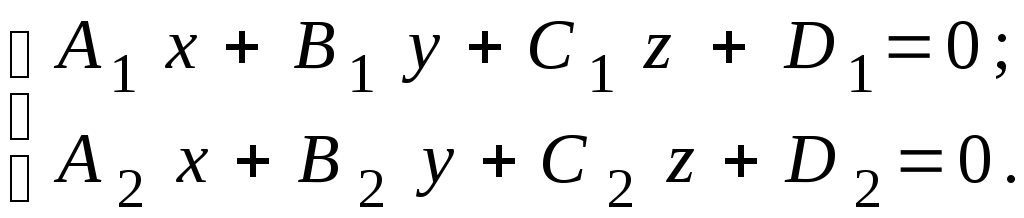(4.12)

2.Каноническое уравнениепрямой

Положение прямой в пространстве

можно определить также данной точкой

, лежащей на прямой и

направляющим вектором

(рис. 4.3). Тогда получим каноническое

уравнение прямой

. (4.13)

Если знаменатели (4.13) разделить на , то получим

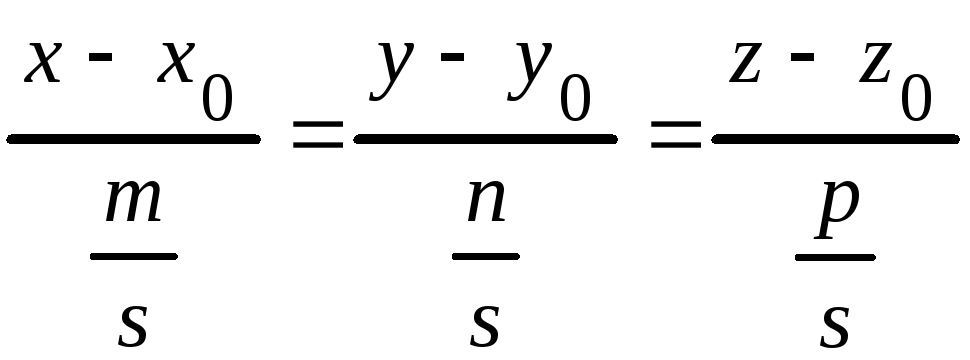, или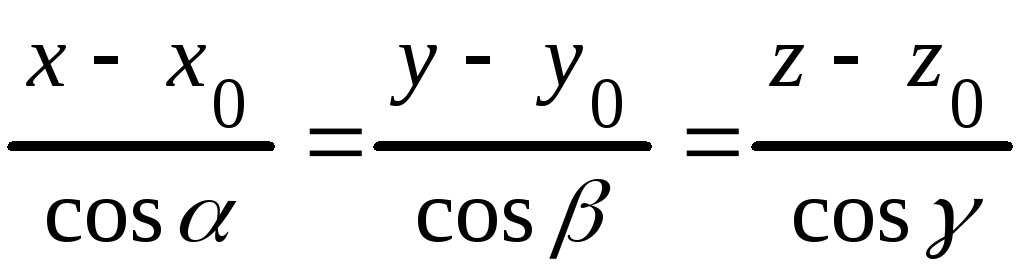, (4.14)

где ,,углы, образованные прямой с осями координат,,.

3. Параметрические уравнениепрямой, проходящей через точкув направлении вектораимеют вид

(4.15)

где параметр.

4. Уравнение прямой, проходящей черездве заданные точкии

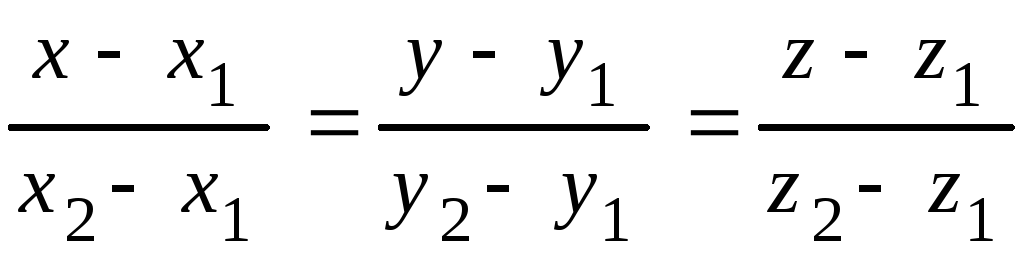. (4.16)

. Основные задачи на прямую линию

1. Угол между двумя прямыми, заданными каноническими уравнениями

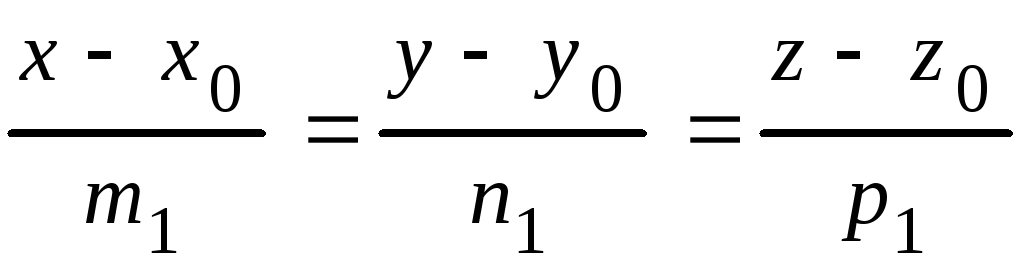и

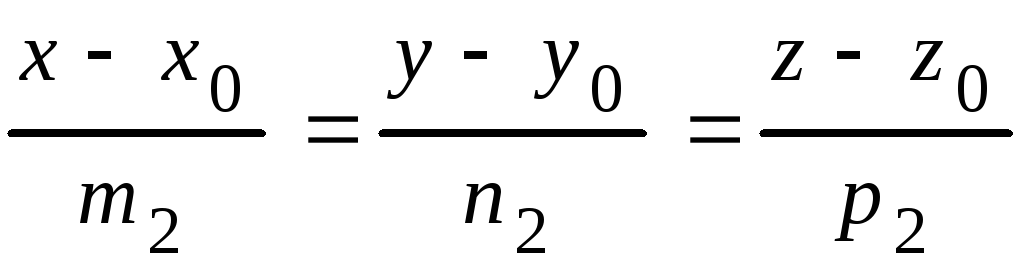
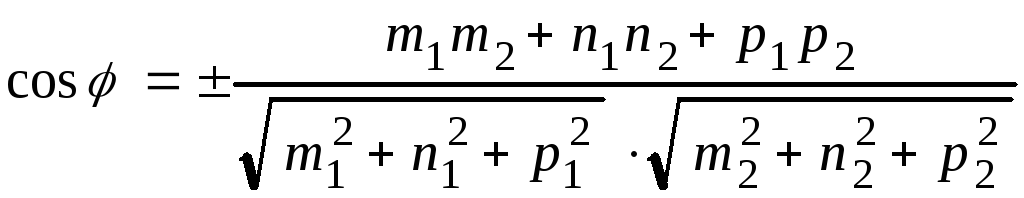, (4.17)

Знак « + » соответствует выбору острого угла, знак « – » – тупого угла.

. Если прямая задана каноническими уравнениями

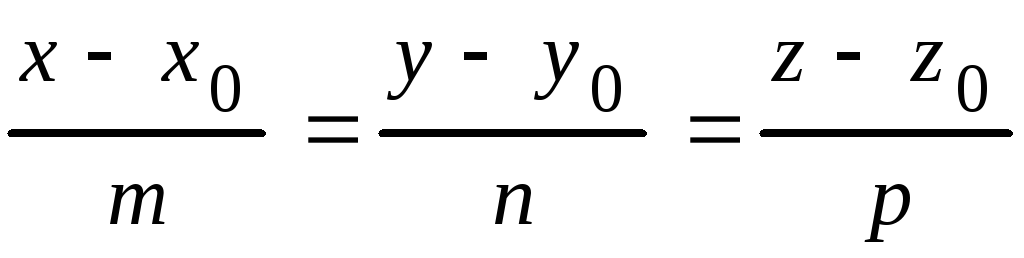, а плоскость , то:

1. Координаты точки пересечения прямой и плоскости находится по формулам

(4.18)

где параметр . (4.19)

2. Угол между прямой и плоскостью (рис. 4.4)

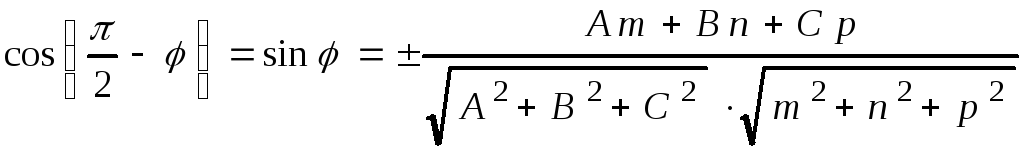. (4.20)

3. Уравнение пучка плоскостей

. (4.21)

4. Условие параллельностипрямой и плоскости

. (4.22)

5. Условие перпендикулярностипрямой и плоскости

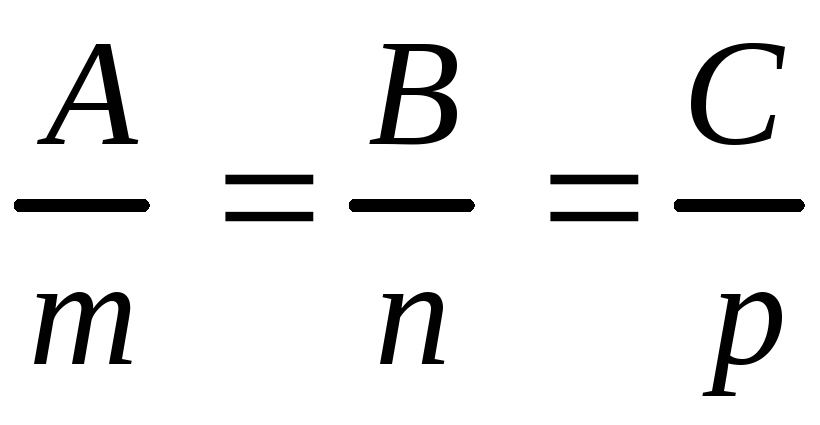. (4.23)

4.2.1. Решение типовых примеров заданий 9, 10 ргр

1. Заданы прямая и координаты точки. 1. Написать канонические уравнения:а) прямой, заданной пересечением двух плоскостей,б) прямой, проходящей через заданные точки.

2. Найти острый угол между этими прямыми.

,.

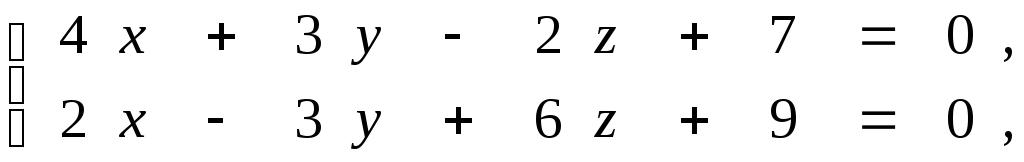
Решение. 1.а) Найдем какую-нибудь точуна данной прямой. Для этого положим в обоих уравненияхи решим систему уравнений

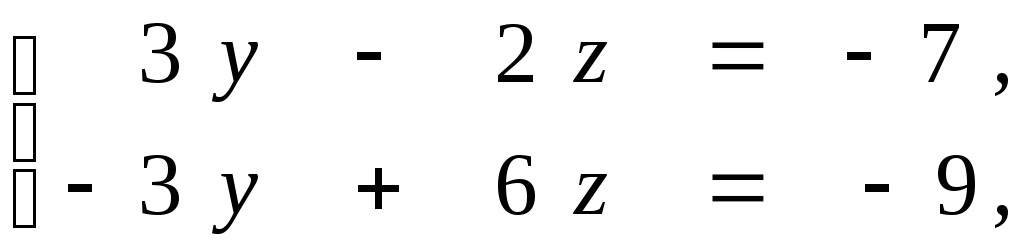
Таким образом, точка принадлежит данной прямой.

Направляющий вектор найдем по формуле

,

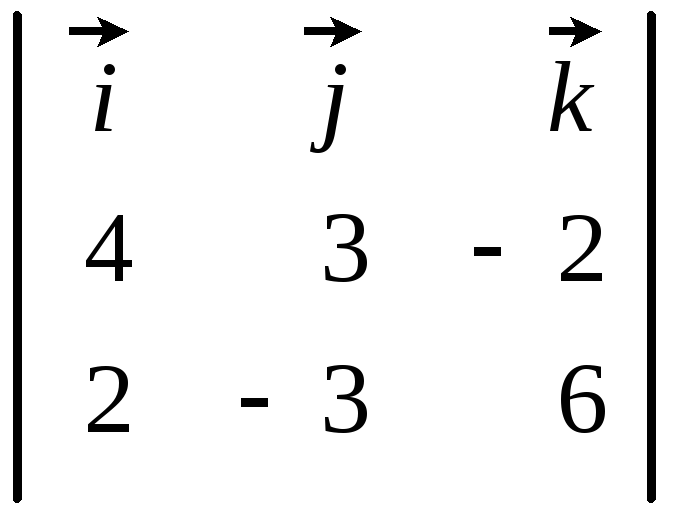
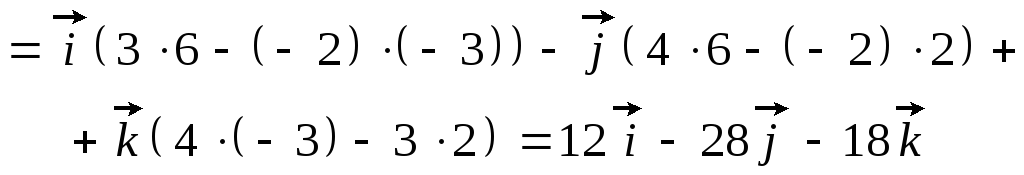то есть он имеет координаты , или, разделив на общий множитель, получим.

Тогда запишем каноническое уравнение прямой

.

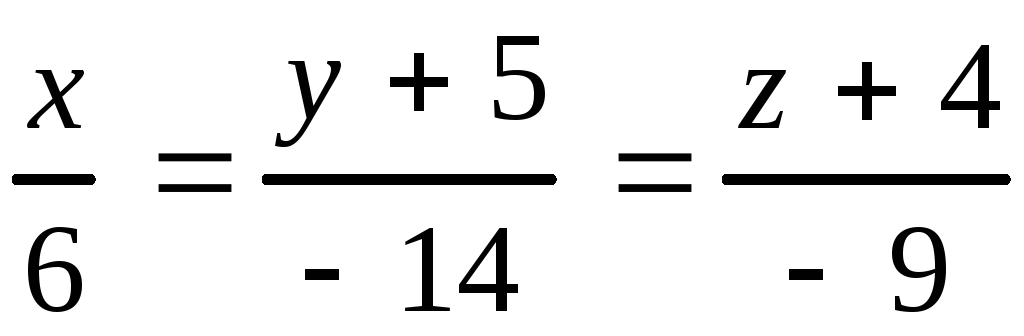б) Уравнение прямой, проходящей через две заданные точкииимеет вид (4.16). По условию задачи,, поэтому искомое уравнение

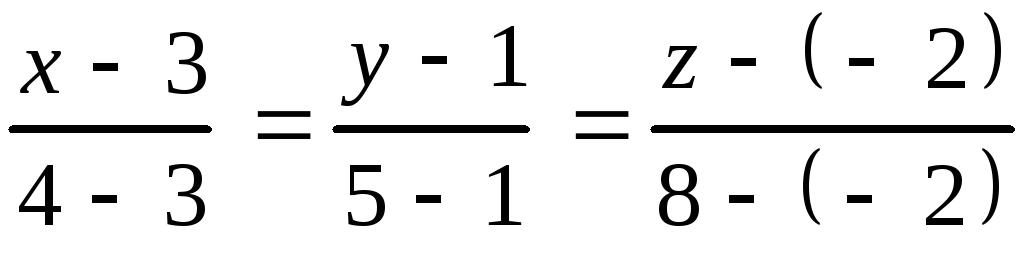или.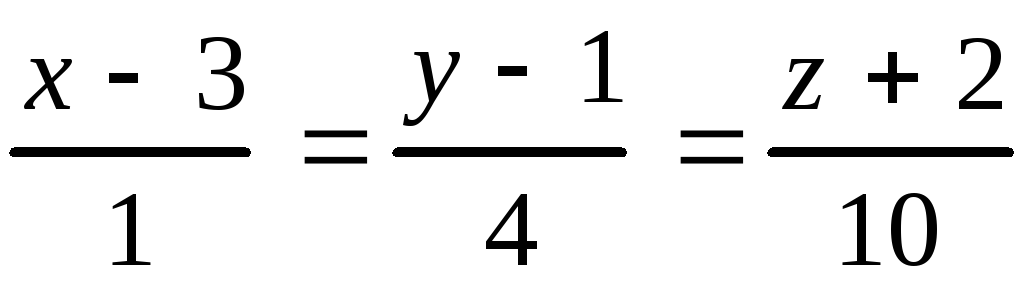

2. Угол между двумя прямыми найдем по формуле (4.17)

.

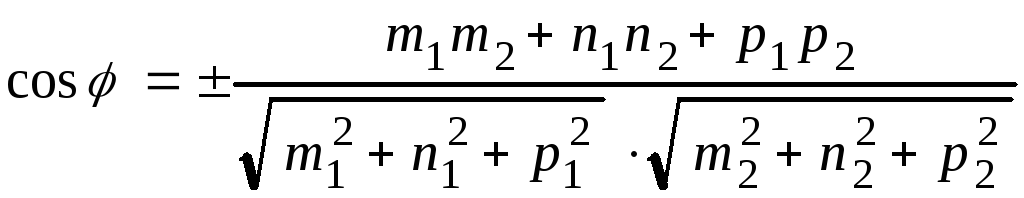В нашем случае ,,;,,.

Косинус острого угла положителен, поэтому

.

;рад;.

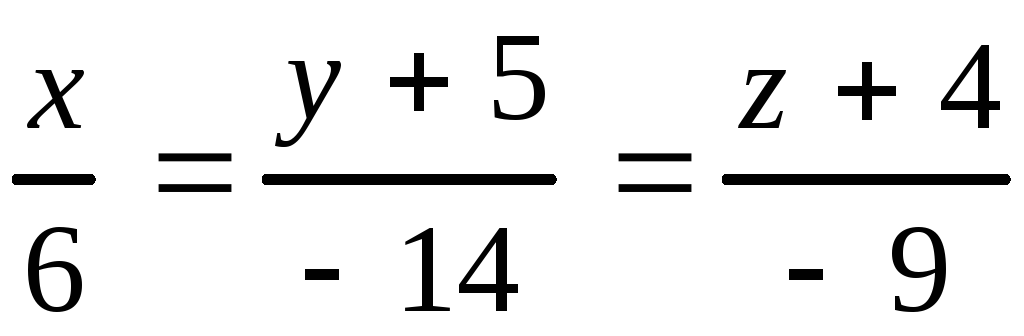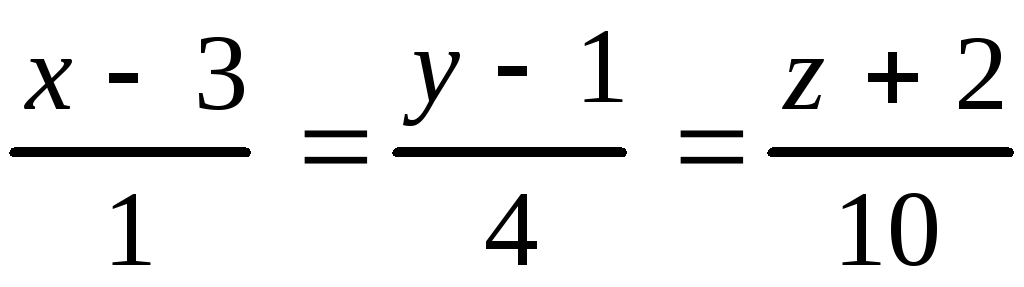Ответ: 1.а),б). 2..

2. Заданы прямая в пространстве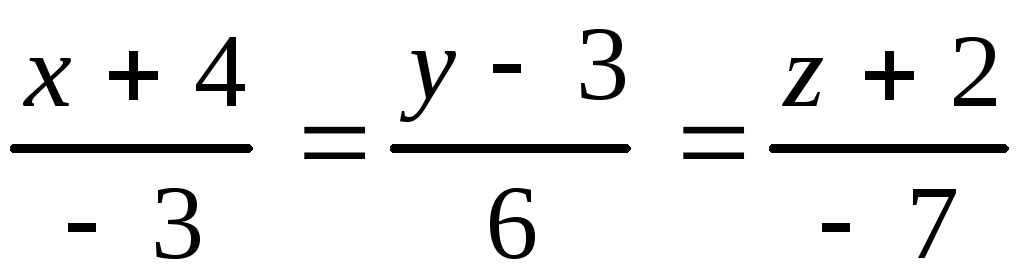и плоскость.

Найти: 1) точку пересечения прямой и плоскости; 2) острый угол между прямой и плоскостью.

Решение. 1) Найдем точку пересечения прямой и плоскости. Для этого определим параметрпо формуле (4.19).

В нашем случае

.

Теперь найдем координаты точек пересечения прямой и плоскости

; ; .

2) Угол между прямой и плоскостью определим по как

.

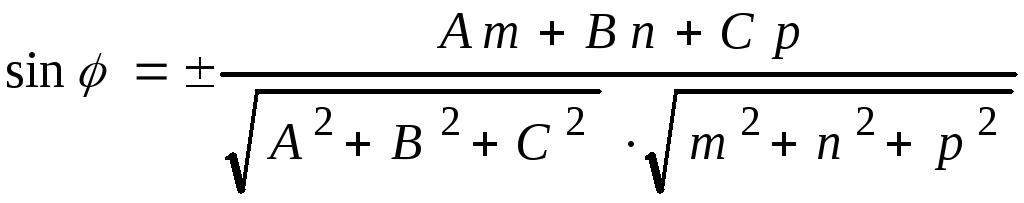Синус острого угла положителен, поэтому

.

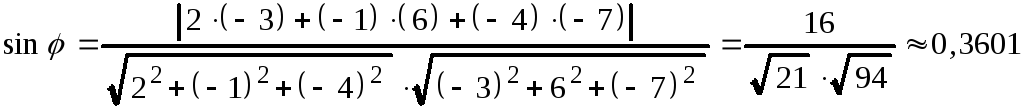рад;.

Ответ:1). 2).