PFE / ПФЭ / Глава7Б

227

7 . Пучково-плазменные усилители и генераторы

7.2.2. Усиление и генерация колебаний в пучково-плазменных системах

7.2.2.1. Исходные уравнения

В предыдущем разделе были рассмотрены физические основы усиления колебаний в безграничной плазме, пронизываемой безграничным пучком. В реальности же при разработке плазменных усилителей и генераторов необходимо исследование взаимодействия ограниченных по размерам плазмы и потока электронов.

Предположим, что плазма и электронный пучок заключены в круглый металлический волновод радиуса R, ось которого совпадает с осью x. Пусть плазма заполняет волновод однородно по его радиусу. Пучок же будем считать узким трубчатым, т. е. функция распределения электронов пучка при и , где – средний радиус пучка, а  – его толщина. Приведем расчёт данной системы согласно [20].

Исходными уравнениями при расчете электродинамических структур плазменных усилителей и генераторов являются уравнения электромагнитного поля и уравнения движения электронов плазмы и пучка. Движением ионов плазмы можно пренебречь, поскольку интересующие нас процессы протекают за времена, много меньше характерного времени движения тяжелых по сравнению с электронами ионов. Роль ионов при этом сводится лишь к нейтрализации статического электрического заряда в плазме. При записи исходных уравнений удобно пользоваться цилиндрическими координатами . Для упрощения математических выкладок ограничимся рассмотрением взаимодействия электронного пучка только с аксиально-симметричной плазменной волной, т. е. будем считать, что поле волны не зависит от угла . Если к тому же вся система помещена в сильное внешнее постоянное магнитное поле , замагничивающее как электроны плазмы, так и электроны пучка, то движение электронов можно рассматривать как одномерное (только вдоль оси x). В этом случае уравнения Максвелла преобразуются к виду

;

; (7.66)

где – компоненты электрического и магнитного поля волны, а j_p и j_b – индуцированные высокочастотные составляющие плотности токов в плазме (plasma) и электронном пучке (beam). Чтобы замкнуть систему уравнений (7.66), необходимо получить уравнения для определения плотностей токов j_p и j_b..

Поскольку средняя тепловая скорость электронов плазмы всегда много меньше направленной скорости электронов пучка, то ею можно пренебречь и считать температуру электронов равной нулю. В этом случае для описания движения электронов плазмы можно использовать уравнения холодной нерелятивистской плазмы в гидродинамическом приближении

(7.67)

где n_p и v_p – плотность и скорость электронов плазмы, а e и m₀ –заряд и масса электрона. При этом плотность электронного тока в плазме определяется соотношением

(7.68)

Для описания движения электронов пучка можно использовать бесстолкновительное кинетическое уравнение – уравнение Власова

(7.69)

где – функция распределения электронов пучка, – импульс электрона. Высокочастотная составляющая плотности тока электронного пучка определяется интегралом

, (7.70)

где – высокочастотная составляющая функции распределения . Постоянную составляющую тока пучка можно не учитывать, поскольку при инжекции электронного пучка в плазму в последней индуцируется ток, компенсирующий постоянную составляющую тока пучка.

Довольно сложная система уравнений (7.66)–(7.70) может быть существенно упрощена. Первое упрощение связано с возможностью линеаризации уравнений движения электронов плазмы (7.67). Такая возможность следует из того, что на электроны плазмы, не имеющие направленной скорости, электромагнитные волны, распространяющиеся с большой фазовой скоростью (порядка направленной скорости электронов пучка), не оказывают в среднем существенного влияния. Учитывая сказанное, из уравнений (7.67), (7.68) в линейном приближении получаем следующее уравнение для тока в плазме

, (7.71)

где – ленгмюровская частота электронов плазмы, а – их равновесная плотность.

При пучок слабо возмущает радиальную структуру поля волновода, вследствие чего решение уравнений (7.66) можно искать в виде

;

; (7.72)

,

где и – функции Бесселя нулевого и первого порядка соответственно, а – какой-либо корень уравнения Такой вид решения можно задать потому, что при уравнения (7.66), (7.71) с граничным условием

(7.73)

имеют следующее решение:

;

; (7.74)

где  и k связаны дисперсионным уравнением

(7.75)

Подставив (7.72) в уравнения (7.66), (7.69), (7.71), домножив третье уравнение (7.66) на и проинтегрировав его по r от нуля до R, получим следующую систему уравнений:

;

;

; (7.76)

;

где . При выводе третьего уравнения (7.76) было использовано неравенство позволяющее применить теорему о среднем при интегрировании по r.

7.2.2.2. Линейная теория плазменных усилителей и генераторов

Линеаризуем систему уравнений (7.76). Для этого, очевидно, необходимо линеаризовать только уравнение Власова для электронов пучка, так как все остальные уравнения системы линейны. Линеаризованное уравнение Власова имеет вид

(7.77)

где – равновесная функция распределения электронов пучка. Будем считать, что в равновесии электронный пучок является моноэнергетическим, так что

(7.78)

где а и v – невозмущенные значения плотности и скорости электронов в пучке.

Полагая из (7.77) находим

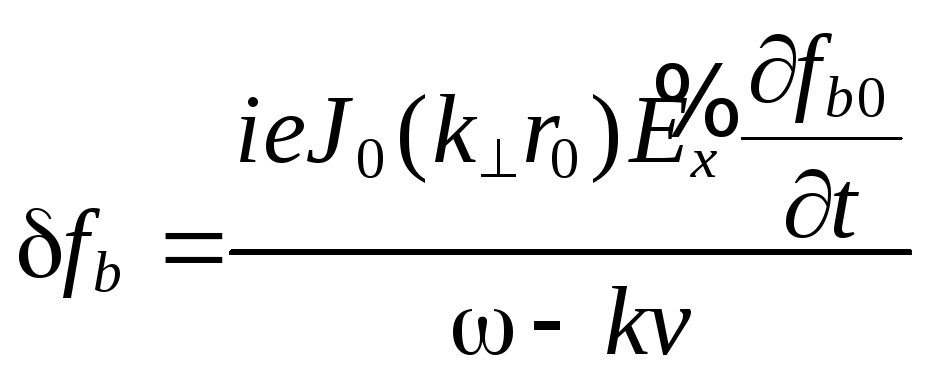. (7.79)

Используя далее определение тока пучка и свойства дельта-функции, получим

(7.80)

где – ленгмюровская частота электронов пучка.

Подставляя (7.80) в систему уравнений (7.76) и полагая все переменные этой системы пропорциональными получим однородную систему алгебраических уравнений, из которой следует дисперсионное уравнение

(7.81)

где

При уравнение (7.81) переходит в (7.75).

Прежде всего убедимся, что в плазменном волноводе действительно существуют волны с фазовой скоростью, меньшей скорости света с. Для этого рассмотрим уравнение (7.75), соответствующее отсутствию электронного пучка, и разрешим его относительно k. Решение этого уравнения имеет вид где

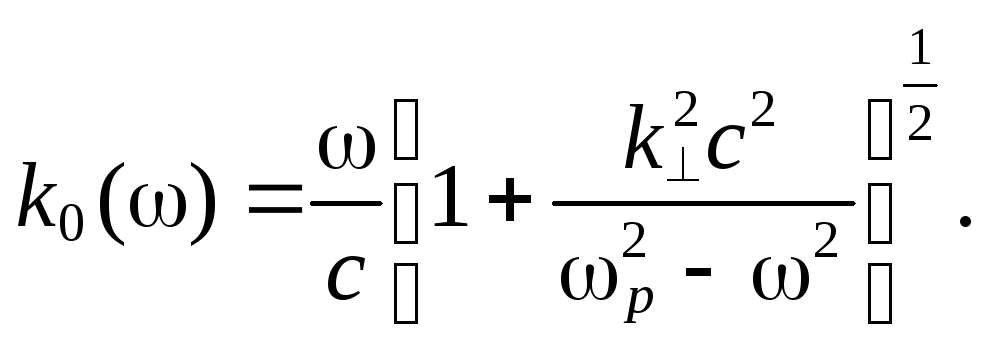(7.82)

Отсюда следует, что фазовая скорость плазменных волн равна

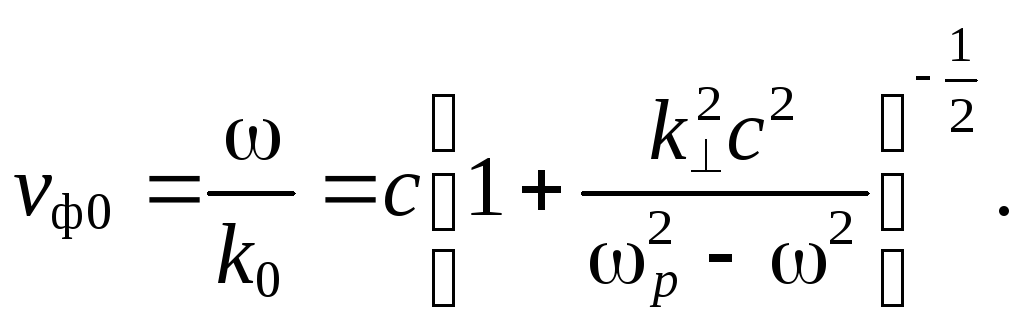(7.83)

Легко видеть, что в области частот фазовая скорость меньше скорости света с. Групповая скорость рассматриваемых волн равна

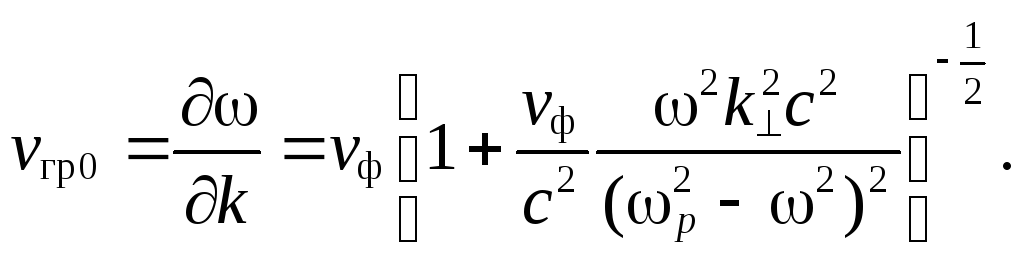(7.84)

Групповая скорость всегда меньше фазовой. Двум решениям соответствуют две волны, распространяющиеся в противоположные стороны.

При наличии пучка электронов, когда уравнение (7.81) является уравнением четвертого порядка относительно k и имеет четыре корня где n = 1, 2, 3, 4. Общее решение линеаризованной системы уравнений (7.76) представляет собой суперпозицию четырех волн с волновыми числами . Так, например, компоненту поля можно записать в виде

(7.85)

где – произвольные постоянные.

Сравнительно просто показать, что в случае электронных пучков малой плотности, когда выполнено неравенство

(7.86)

где , приближенное решение уравнения (7.81) имеет вид

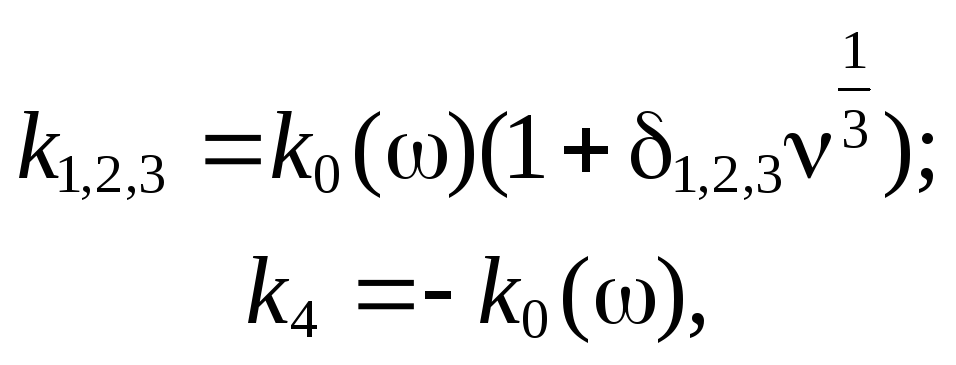(7.87)

где – корни кубического уравнения

(7.88)

а Величину , пропорциональную разности между фазовой скоростью невозмущенной плазменной волны и скоростью электронов пучка, будем называть расстройкой. Таким образом, наличие электронного пучка приводит к расщеплению плазменной волны с волновым числом на три волны с близкими волновыми числами .

Рассмотрим вопрос о направлении распространения найденных четырех волн. Для этого определим их групповые скорости. Что касается волны с волновым числом , то ее групповая скорость, очевидно, равна . Эта волна распространяется навстречу электронному пучку без изменения своей амплитуды. Групповые скорости остальных трех волн (n = 1,2,3) определяются выражением

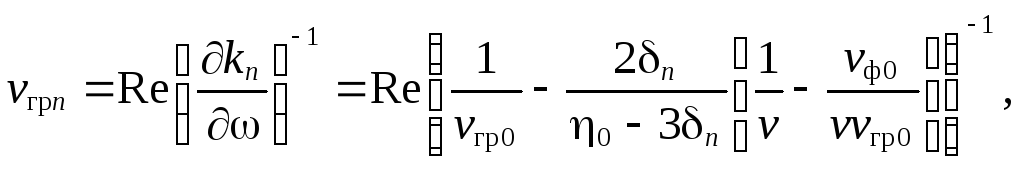(7.89)

при выводе которого использованы соотношения (7.87), (7.88). В частном случае нулевой расстройкой из (7.89) имеем

(7.90)

Качественная зависимость групповых скоростей от расстройки представлена на рис. 7.3. Из рисунка видно, что все групповые скорости положительны, т. е. соответствующие волны распространяются в направлении движения электронов пучка.

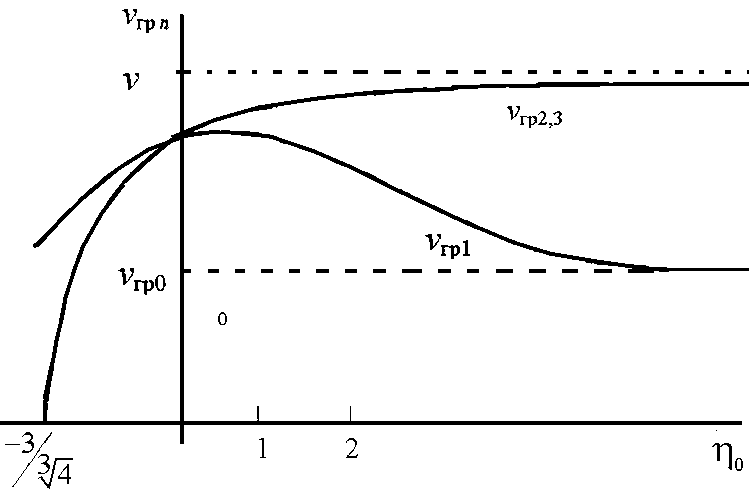
Рис. 7.3. Зависимость групповых скоростей волн от расстройки

Анализ уравнения (7.88) показывает, что при оно имеет два комплексно сопряженных корня. Это означает, что одна из волн, распространяющихся в направлении пучка, усиливается, а другая затухает. Максимум усиления достигается при нулевой расстройке, когда

(7.91)

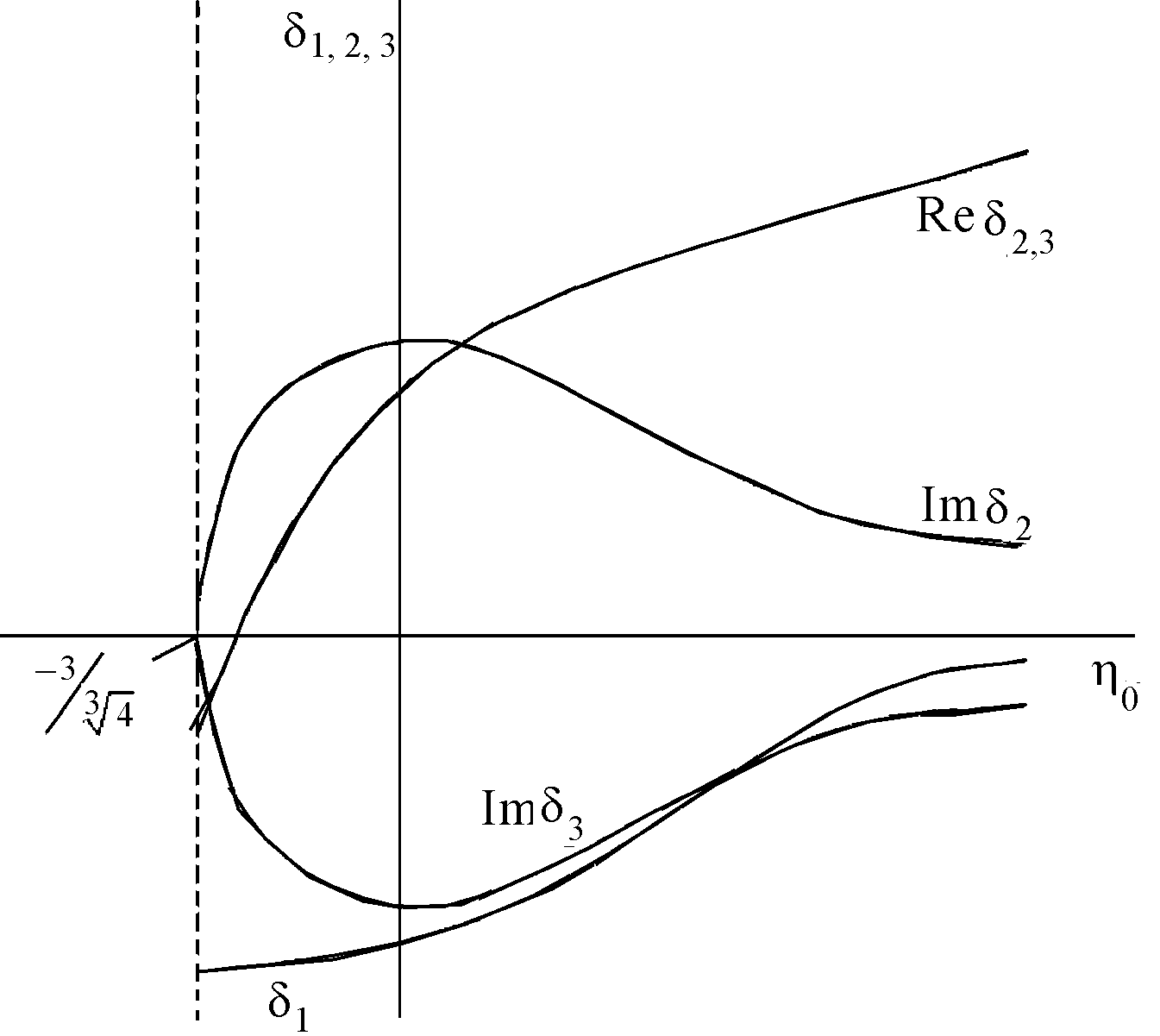
Рис. 7.4. Зависимость от расстройки

Зависимость от расстройки показана на рис. 7.4. Как следует из рисунка и формул (7.91), усиливается волна с волновым числом . Так как то фазовая скорость усиливаемой волны, равная меньше скорости пучка v, т. е. электронный пучок обгоняет волну и, следовательно, отдает ей свою энергию.

Рассмотрим теперь плазменный генератор, представляющий собой отрезок волновода длины L, снабженный в сечении x = 0 металлической сеткой, прозрачной для электронов пучка и непрозрачной для волн. На конце волновода при x = L имеется какое-либо излучающее устройство.

Для определения условий самовозбуждения такого генератора необходимо задать граничные условия при x = 0 и x = L. Рассмотрим сначала границу x = 0, на которой обращается в нуль тангенциальная составляющая поля волны . При x = 0 равны нулю возмущения плотности тока и плотности заряда в пучке, так как на вход системы пучок поступает невозмущенным. Таким образом, из (7.85) (7.80), (7.76) и уравнения непрерывности получаем следующие граничные условия:

;

; (7.92)

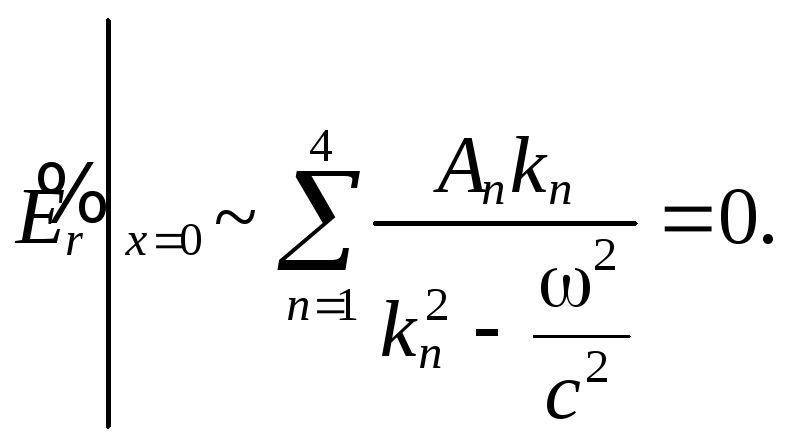
При записи условий (7.92) учтено, что волна с волновым числом , распространяющаяся навстречу пучку, возмущает пучок достаточно слабо.

Учитывая теперь выражения (7.87), уравнение (7.88) и неравенство (7.86), после несложных преобразований приведем условия (7.92) к виду

(7.93)

где

; ;

Коэффициенты имеют смысл коэффициентов трансформации волны с волновым числом в волны с волновыми числами на границе x = 0. Легко убедиться, что

На границе x = L происходит обратная трансформация, а именно, волны с волновыми числами трансформируются в волну с волновым числом . В самом общем виде этот процесс может быть описан соотношением

(7.94)

где – комплексные коэффициенты отражения волн. Вычисление конкретных значений коэффициентов представляет собой сложную задачу, для решения которой необходимо прежде всего задать какую-либо модель выходного устройства. Отметим только, что при выполнении неравенства (7.86) все коэффициенты близки к – коэффициенту отражения от выходного устройства волны, распространяющейся в волноводе без электронного пучка. Последний обычно бывает известен из эксперимента.

Подставляя (7.93) в (7.94) и полагая , получим характеристическое уравнение для определения комплексных собственных частот системы

(7.95)

В отсутствие пучка решением уравнения (7.95) является набор собственных частот с положительной мнимой частью. Это означает, что энергия поля в резонаторе затухает вследствие излучения через выходное устройство. Найдем такое значение , при котором затухание будет скомпенсировано поступлением энергии от электронного пучка, т. е. хотя бы одно из значений  будет действительным.

Рассмотрим наиболее интересный случай, когда усиление второй волны на длине резонатора значительно, т.е. выполнено неравенство

(7.96)

При выполнении этого неравенства на границе x = L можно пренебречь волнами с волновыми числами и . Учитывая это, запишем уравнение (7.95) в виде системы двух уравнений, разделяя действительные и мнимые части:

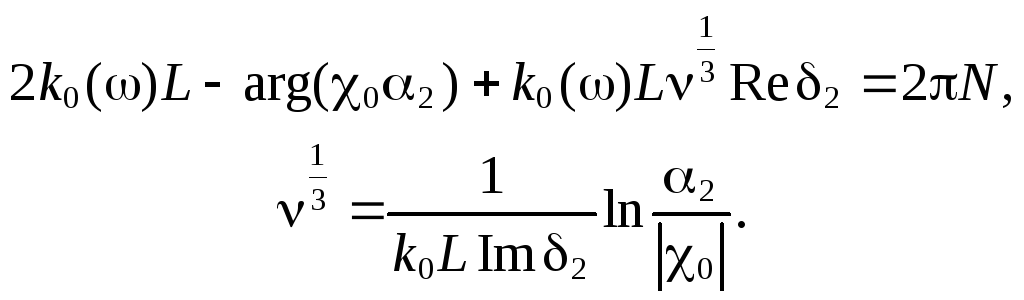(7.97)

Уравнения (7.97) позволяют определить пороговое значение ленгмюровской частоты электронов пучка , при котором начинается самовозбуждение колебаний в системе на некоторой собственной частоте . Зависимость от не является монотонной. При , наиболее близком к значению , соответствующему нулевой расстройке , коэффициент усиления максимален и, следовательно, минимально. Если , то, как следует из (7.91) и (7.94), и уравнения (7.97) принимают вид

(7.98)

где N₀ – значение N, при котором .