PFE / ПФЭ / Глава7Б-1

228

7.2.2. Линейная теория плазменных усилителей и генераторов.

В предыдущем разделе были рассмотрены неустойчивости, возникающие в безграничной плазме, пронизываемой безграничным пучком, которые положены в основу принципа действия плазменных усилителей и генераторов СВЧ. В действительности же, при разработке электродинамических структур данных приборов необходимо исследование взаимодействия ограниченных по размерам плазмы и потока электронов. Как правило, это цилиндрические плазменные волноводы, находящиеся во внешнем магнитном поле, направленном вдоль оси волновода, пронизываемые цилиндрическим или трубчатым электронным пучком – структуры с осевой симметрией. Исходными уравнениями для их расчёта служат уравнения Максвелла, записанные для компонент электрического и магнитного поля в цилиндрической системе координат, и уравнения движения электронов плазмы и пучка. Внешнее магнитное поле замагничивает электроны пучка и плазмы, поэтому их движение можно считать одномерным - вдоль оси волновода. Движением ионов плазмы можно пренебречь, поскольку интересующие нас процессы протекают за времена, много меньше характерного времени движения тяжелых по сравнению с электронами ионов. Роль ионов при этом сводится лишь к нейтрализации статического электрического заряда в плазме.

В таком случае, уравнения Максвелла, записанные для аксиально-симметричного поля волны, т.е. не зависящего от угла φ (производная по φ равна нулю) имеют вид:

(7.66)

где - компоненты электрического и магнитного поля волны, а j_p и j_b - индуцированные высокочастотные составлящие плотности токов в плазме и электронном пучке соответственно. Чтобы найти решение системы уравнений (7.66), необходимо выразить плотности токов в плазме j_p и электронном пучке j_b через компоненты поля.

Выражение для плотности тока электронов плазмы можно определить, используя уравнения движения электронов холодной нерелятивистской плазмы в гидродинамическом приближении, которое справедливо для высокочастотных волн, когда их фазовая скорость много больше средней тепловой скорости электронов

(7.67)

(7.68)

где n_p и v_p - плотность и скорость электронов плазмы. Линеаризуя уравнения (7.67) и (7.68), т.е подставляя в них (<<) и (<<), где и - возмущение плотности и скорости электронов плазмы пропорцианальные ~ пренебрегая членами второго порядка малости, а также учитывая, что j_p=en_pv_p и ≈0, получим

(7.69)

где - ленгмюровская частота электронов плазмы, а - их равновесная плотность.

Выражение для плотности тока электронного пучка определяется интегралом

(7.70)

где - высокочастотная составляющая функции распределения электронов пучка , p - импульс электрона, определяемая из бесстолкновительного кинетического уравнения - уравнения Власова

(7.71)

Постоянную составляющую тока пучка можно не учитывать, поскольку при инжекции электронного пучка в плазму в последней индуцируется ток её компенсирующий.

Замкнутая система уравнений (7.66), (7.69), (7.70) и (7.71) описывает поле аксиально-симметричных волн в холодной плазме, пронизываемой электронным потоком с функцией распределения f_b(t,x,p).

Найдем выражения для компонент поля в круглом металлическом волноводе радиуса R, полностью заполненном однородной плазмой, в отсутствие пучка, т.е когда j_b=0. Тогда к уравнениям (7.66) и (7.69) необходимо добавить граничное условие на поверхности металла

(7.72)

и условие ограничения амплитуды поля на оси волновода

(7.73)

Полагая все переменные пропорциональными ~ для компонент поля из уравнений (7.66) и (7.69)получим:

(7.74)

где и - функции Бесселя нулевого и первого порядка соответственно. Из граничного условия (7.72) следует, что - какой-либо корень уравнения Кроме того,

(7.75)

Уравнение (7.75) есть дисперсионное уравнение, связывающее частоту  и волновой вектор k различных типов волн (), которые могут распространяться в круглом волноводе радиуса R, полностью заполненном однородной холодной плазмой. Решение этого уравнения

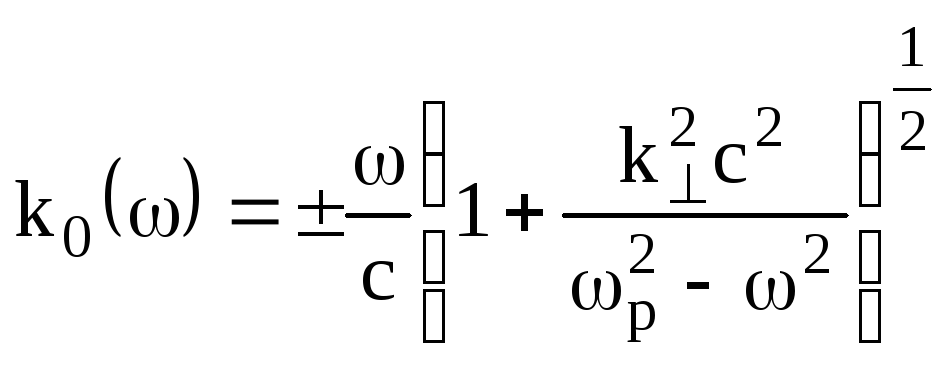, (7.76)

соответствует двум волнам, распространяющимся в противоположные стороны. Фазовая скорость этих волн равна

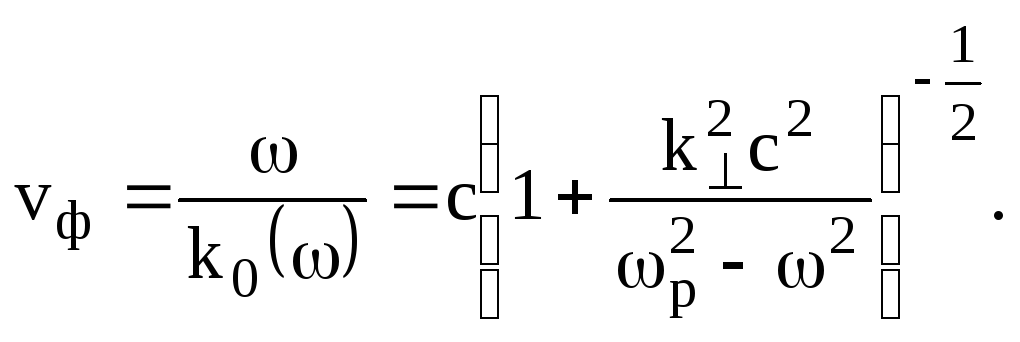(7.77)

Из (7.77) следует, что в области частот , фазовая скорость меньше скорости света с. Это обстоятельство и позволяет использовать плазменные волноводы в качестве замедляющих структур усилителей и генераторов СВЧ.

Пусть теперь плазменный волновод пронизывается электронным пучком. Тогда, для решения системы уравнений (7.66) и (7.69) необходимо задать геометрию пучка, функцию распределения f_b и определить плотность тока пучка из уравнений (7.70) и (7.71). В случае узкого трубчатого пучка со средним радиусом и толщиной , распространяющегося в круглом металлическом волноводе радиуса R (), полностью заполненном однородной плазмой, учитывая (7.74), решение уравнений (7.66) можно искать в виде [19]:

(7.78)

Тогда, подставив (7.78) в уравнения (7.66), (7.69) и (7.71), домножив третье уравнение (7.66) на и проинтегрировав его по r от нуля до R, получим следующую систему уравнений:

(7.79)

где При выводе третьего уравнения (7.79) было использовано неравенство позволяющее применить теорему о среднем при интегрировании по r.

Для определения плотности тока пучка j_b линеаризуем уравнение Власова для электронов пучка:

(7.80)

где - равновесная функция распределения электронов пучка, - её возмущение. Будем считать, что в равновесии электронный пучок является моноэнергетическим, так что

(7.81)

где а и v₀ - невозмущенные значения плотности и скорости электронов в пучке.

Полагая из (7.80) находим

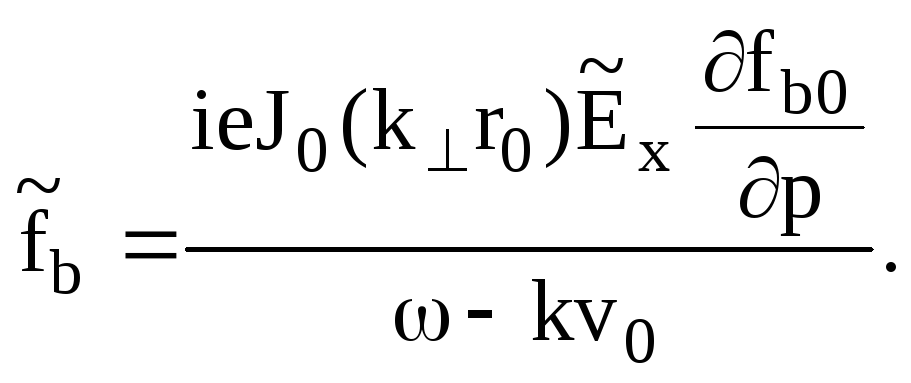(7.82)

Подставляя (7.82) в (7.70) и используя определение тока пучка и свойства дельта - функции, получим

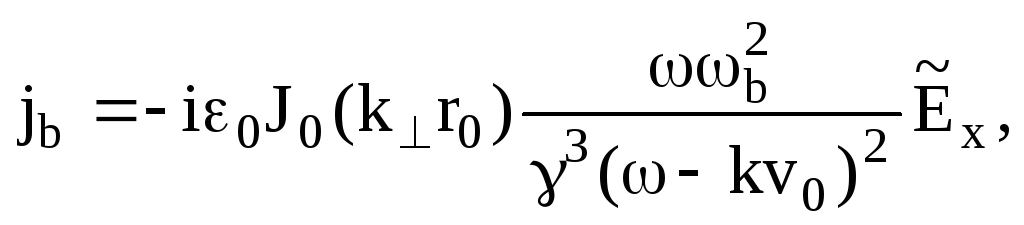(7.83)

где - ленгмюровская частота электронов пучка.

Подставляя (7.83) в систему уравнений (7.79) и полагая все переменные этой системы пропорциональными ~ получим однородную систему алгебраических уравнений для компонент поля аксиально- симметричных волн плазменного волновода с узким трубчатым пучком

(7.84)

,

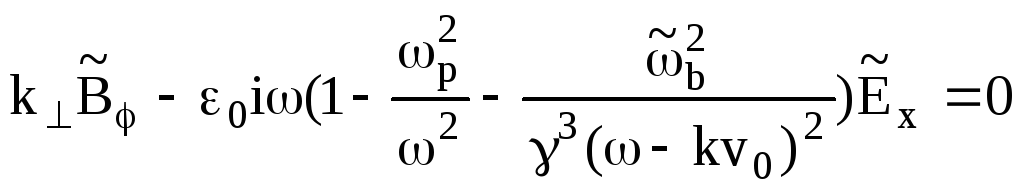где

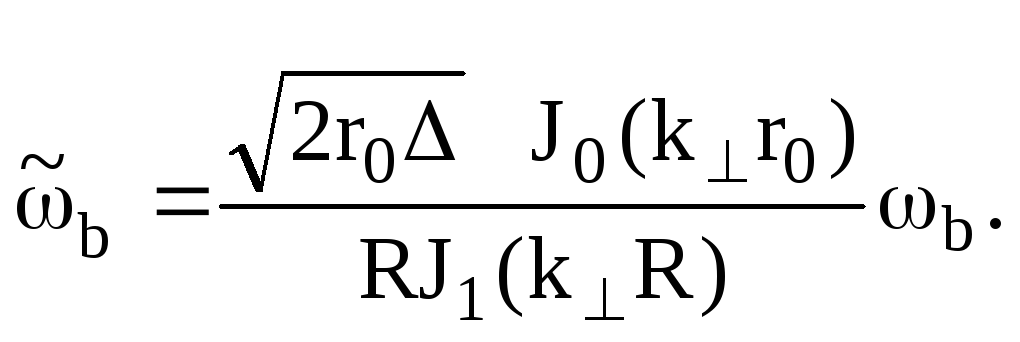
Нетривиальное решение данной системы существует, если определитель системы, составленный из коэффициентов перед искомыми переменными равен нулю, откуда следует дисперсионное уравнение:

(7.85)

В отличие от (7.75), уравнение (7.85) является уравнением четвертого порядка относительно k и имеет четыре корня где n=1,2,3,4. Общее решение линеаризованной системы уравнений (7.79) представляет собой суперпозицию четырех волн с волновыми числами . Так, например, компоненту поля можно записать в виде

(7.86)

где - произвольные постоянные.

Решить дисперсионное уравнение (7.85) аналитически достаточно сложно и приходится прибегать к различным приближениям. Например, в случае электронных пучков малой плотности, когда выполнено неравенство

(7.87)

где 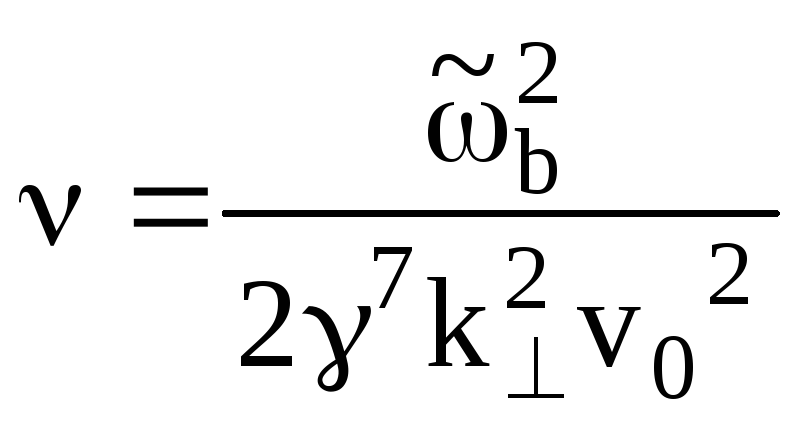, приближенное решение уравнения (7.85) имеет вид [20]:

(7.88)

где - корни кубического уравнения

(7.89)

Величину 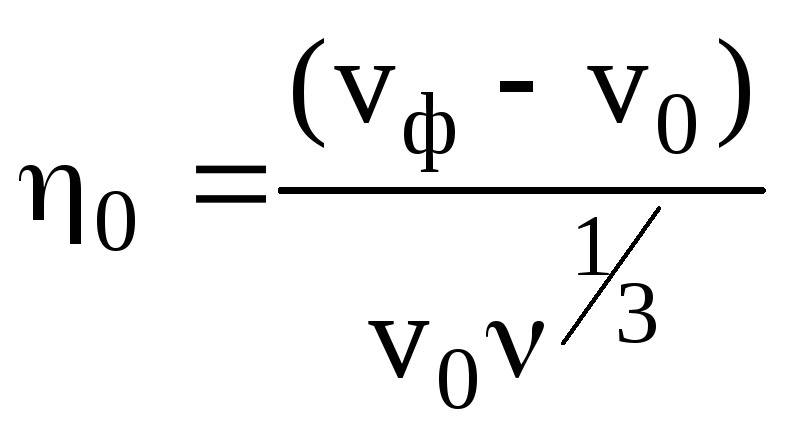, пропорциональную разности между фазовой скорости невозмущенной плазменной волны и скоростью электронов пучка называют расстройкой.

Анализ уравнения (7.89) показывает [19], что при 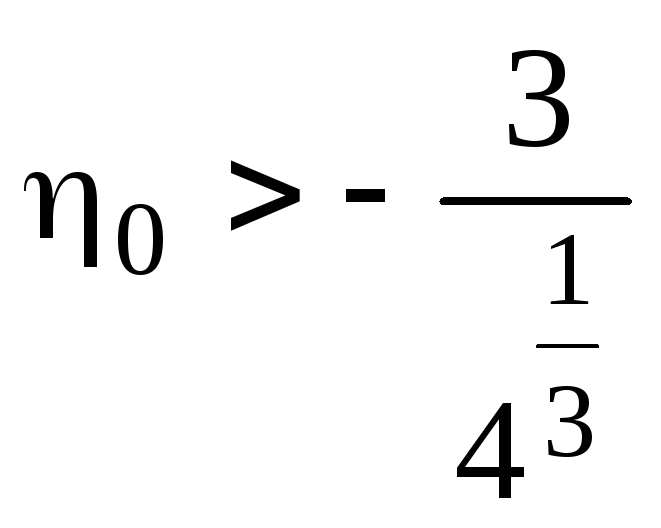оно имеет два комплексно сопряженных корня. Это означает, что одна из волн, распространяющихся в направлении пучка, усиливается, а другая затухает. Максимум усиления достигается в резонансном случае - при нулевой расстройке. Тогда из уравнения (7.89) имеем:

(7.91)

В силу пропорцианальности ~ усиливается волна, имеющая положительную мнимую часть волнового вектора. При этом её волновой вектор и инкремент нарастания амплитуды поля определяются как

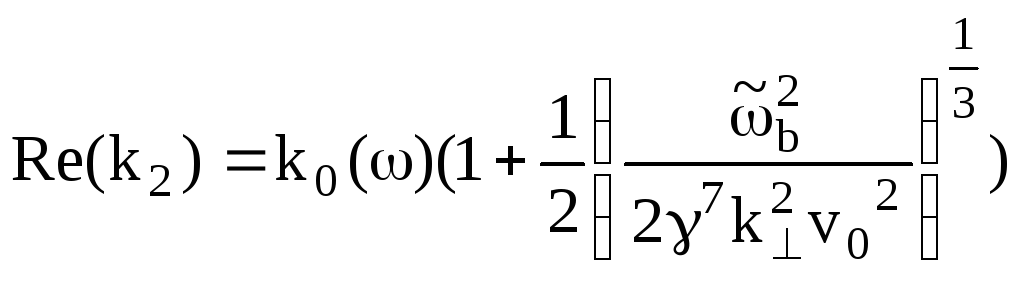(7.92)

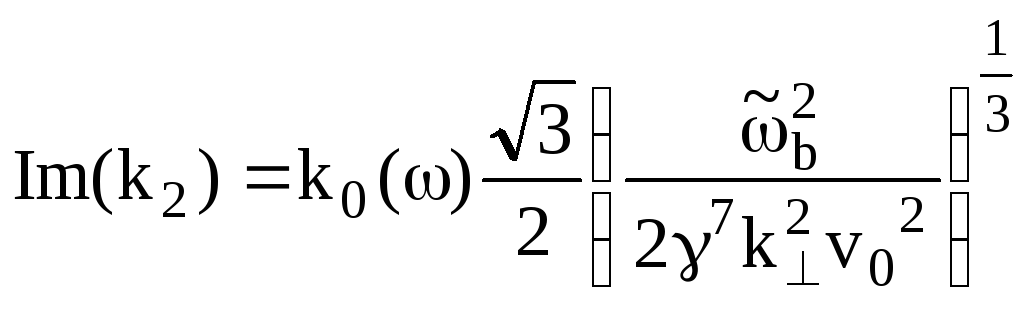(7.93)

В нерезонансном случае, корни уравнения (7.89) зависят от расстройки (рис.7.3). Но, по-прежнему, усиливается волна с волновым числом и инкрементом .

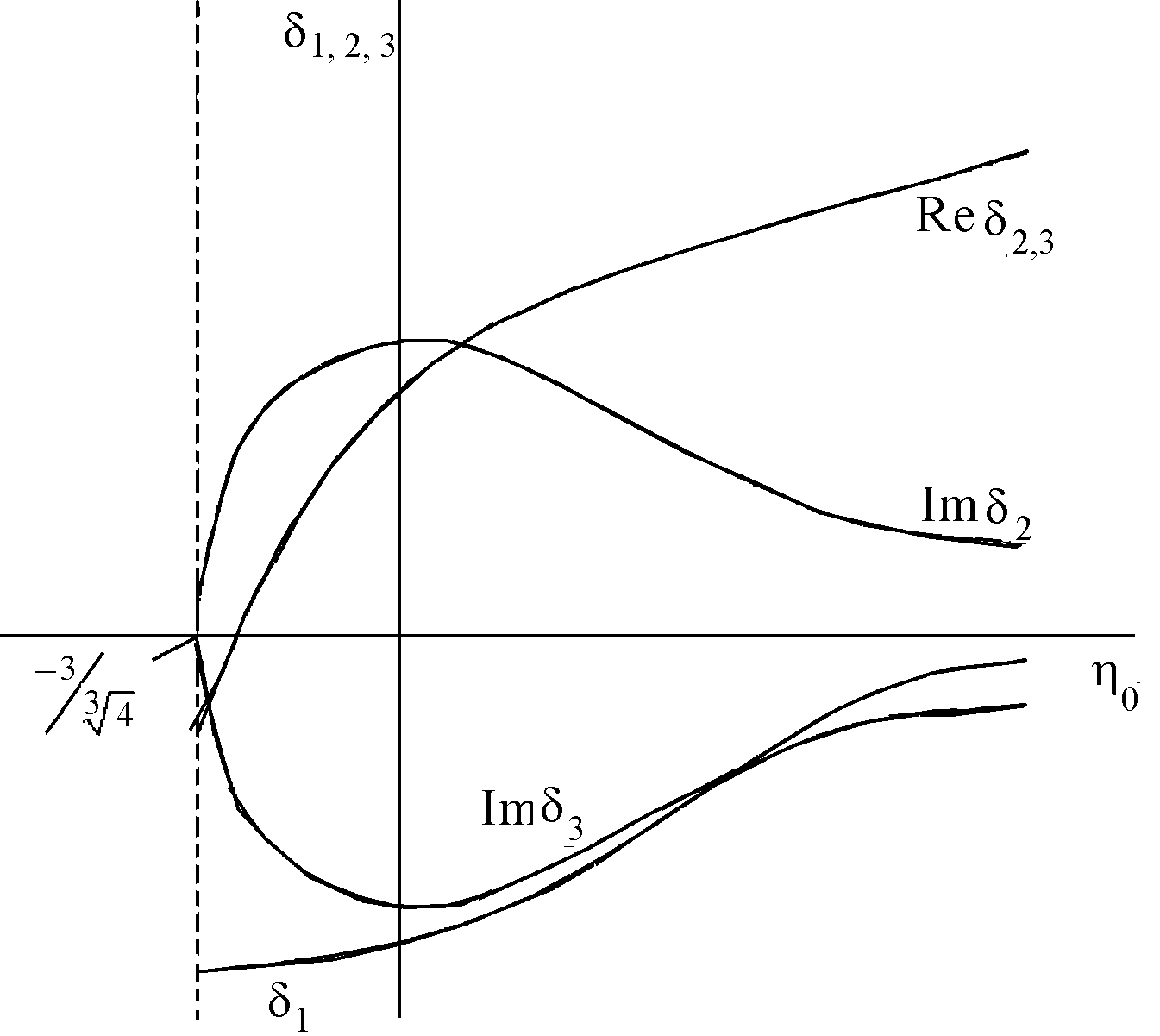
Рис.7.3. Зависимость от расстройки

Таким образом, в плазменном волноводе, пронизываемом электронным пучком, возможно усиление плазменных колебаний по экпоненциальному закону ~e^γx, инкремент которых γ максимален в резонансном случае, т.е. когда фазовая скорость невозмущённой плазменной волны равна скорости электронов пучка, и определяется выражением (7.93).

Отрезок плазменного волновода может служить электродинамической структурой не только усилителя, но и генератора СВЧ колебаний. Для этого требуется создать условия передачи части энергии усиливаемых колебаний от выходной границы отрезка волновода к входной, обеспечивающие самовозбуждение электромагнитных колебаний на собственных частотах. От линейной теории требуется определить значение тока пучка, с которого начинается самовозбуждение колебаний в системе на некоторой собственной частоте.

Пусть электродинамическая структура плазменного генератора представляет собой отрезок волновода длины L, на входе которого при x=0 имеется металлическая сетка, прозрачная для электронов пучка и непрозрачная для волн, а на выходе при x=L происходит частичное излучение наружу и отражение внутрь с коэффициентом отражения . Тогда, на границе x=0 равны нулю тангенциальная составляющая поля волны и возмущения плотности тока и плотности заряда в пучке, так как на вход системы пучок поступает невозмущенным. Из уравнений (7.86) (7.83), (7.74) и уравнения непрерывности заряда пучка граничные условия можно записать следующим образом [19]:

(7.94)

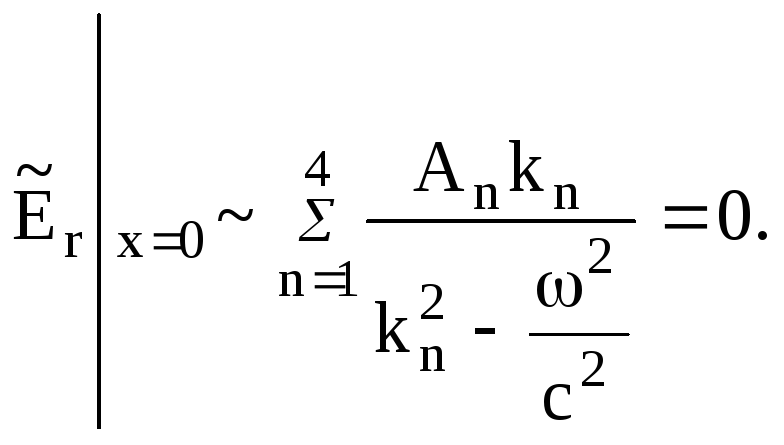
При записи условий (7.94) учтено, что волна с волновым числом , распространяющаяся навстречу пучку, возмущает пучок достаточно слабо.

Граничные условия (7.94) с учётом уравнений (7.87)- (7.89) приводятся к виду

(7.95)

где

Уравнение (7.95) означает, что волна, бегущая навстречу пучку с волновым числом на границе x=0 трансформируется в волны с волновыми числами , амплитуды которых определяются согласно (7.95), при этом

На границе x=L происходит обратная трансформация волн с волновыми числами в волну с волновым числом . Если считать, что для всех трёх волн комплексный коэффициент отражения одинаков, то процесс трансформации волн может быть описан соотношением

(7.96)

или с учётом (7.88):

(7.97)

В случае, когда усиление второй волны на длине отрезка волновода значительно, т.е. выполнено неравенство

, (7.98)

на границе x=L можно пренебречь волнами с волновыми числами и . Учитывая это, и разделяя действительные и мнимые части уравнения (7.97), получим систему двух уравнений:

(7.99)

где N= 0,1,2… . Уравнение (7.99) имеет смысл баланса амплитуд и фаз на границах отрезка плазменного волновода, необходимого для самовозбуждения системы. Первое определяет спектр собственных частот на которых начинается самовозбуждение, а второе – необходимую для этого ленгмюровскую частоту электронов пучка. При наиболее близком к значению , соответствующему нулевой расстройке , коэффициент усиления максимален и, следовательно, минимально. Если , то, как следует из (7.91) и (7.95), и уравнения (7.99) принимают вид

(7.100)

где N₀ - значение N, при котором

Учитывая, что а 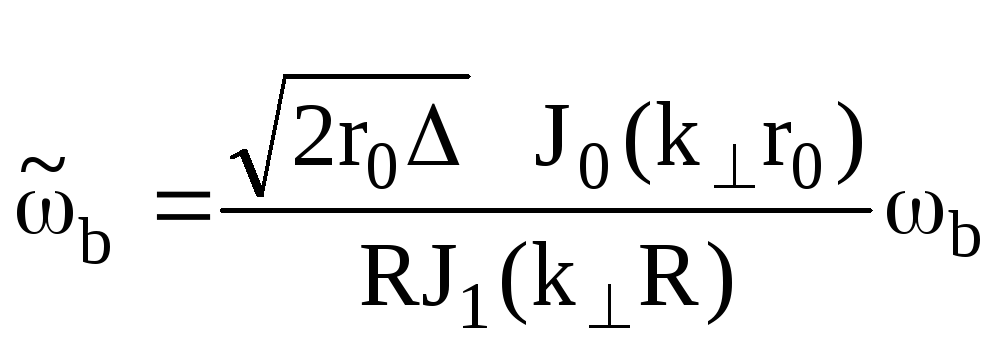, из второго уравнения (7.100) найдем минимальное пороговое значение ленгмюровской частоты электронов пучка, при котором начинается генерация колебаний:

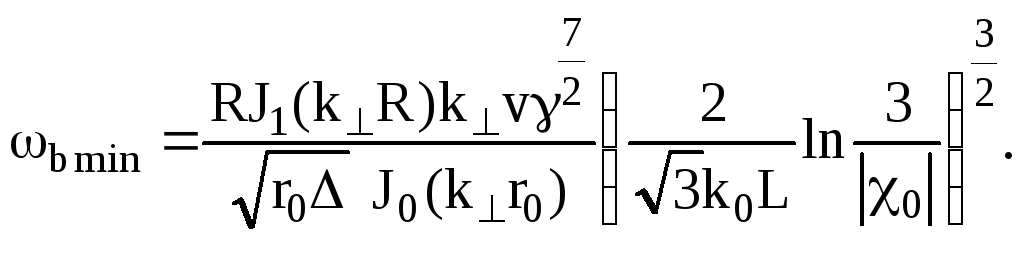(7.101)

Если резонатор не имеет собственной частоты, для которой , т.е. уравнения (7.98) и несовместимы, то пороговое значение будет несколько больше определяемого формулой (7.101).

Из определения ленгмюровской частоты и тогда пороговая плотность тока электронного пучка

. (7.102)

Таким образом, в резонаторе, представляющем собой отрезок плазменного волновода, пронизываемый электронным пучком, начиная с некоторой пороговой плотности электронного пучка, определяемой в линейном приближении выражением (7.102), возможно самовозбуждение, т.е. начало генерации на собственных частотах. Поступающая энергия от электронного пучка компенсирует энергию поля в резонаторе, затухающую вследствие излучения через выходное устройство.