
2.5.2. Конвекционный ток и анализ характеристик отражательного клистрона на основе электронных проводимостей
Анализ спектрального состава сгустков в отражательном клистроне, в принципе, не отличается от такого же анализа в двухрезонаторном клистроне. Как и в двухрезонаторном клистроне, сгустки в отражательном клистроне можно представить в виде периодической последовательности импульсов конвекционного тока. Последнюю, в свою очередь, можно представить в виде суммы постоянной составляющей и бесконечного ряда гармоник, амплитуды которых определяются разложением в ряд Фурье.
Уравнение группирования для отражательного клистрона имеет такой же вид, как для пролетного клистрона, если суммарное время пролета в обоих приборах отсчитывать от момента прохождения резонатора тем невозмущенным электроном, около которого происходит группирование.
В пролетном клистроне начало отсчета соответствовало невозмущенному электрону, пролетавшему середину резонатора при переходе от тормозящего к ускоряющему полупериоду. Около этого электрона происходило в дальнейшем группирование остальных электронов. В отражательном клистроне электроны группируются в каждом периоде около другого невозмущенного электрона, который пролетает через середину резонатора при движении от катода через полупериод, т. е. в момент перехода от ускоряющего полупериода к тормозящему (рис. 2.18).
С учетом вышесказанного уравнение группировки для отражательного клистрона будет иметь такой вид
![]() ,
(2.56)
,
(2.56)
где Q- невозмущенный угол пролета пространства группировки, или угол пролета центра сгустка от второй сетки к отражателю и обратно. Этот угол будет равен
![]() . (2.57)
. (2.57)
Второй член в скобках уравнения (2.56) есть не что иное, как невозмущенный угол пролета зазора электроном, не испытавшего воздействия со стороны высокочастотного поля. Этот угол пролета будем обозначать через q
![]() .
(2.58)
.
(2.58)
Параметр группировки Х для отражательного клистрона будет равен
![]()
![]() ,
(2.59)
,
(2.59)
где М – коэффициент взаимодействия высокочастотного зазора клистрона с электронным потоком.
Уравнение (2.56) аналогично по форме выражению (2.11). Сходство распространяется и на уравнения параметров группирования (2.59) и (2.9). Однако в (2.59) вместо угла пролета в пространстве дрейфа Q имеется разность углов пролета Q и q. Это объясняется тем, что группирование электронов в пространстве тормозящего поля и внутри зазора отражательного клистрона происходит относительно разных электронов, сдвинутых во времени на половину периода.
Конвекционный ток i2, поступающий в резонатор при возвращении электронов из пространства группировки при условии, что электроны не оседают на отражателе, равен
![]() .
(2.60)
.
(2.60)
Таким образом, форма волны конвекционного тока в отражательном клистроне такая же, как и в двухрезонаторном клистроне.
Далее рассмотрим электронную проводимость отражательного клистрона, которая определяется отношением комплексных амплитуд наведенного тока и высокочастотного напряжения.
Мгновенные значения первой гармоники наведенного в резонаторе тока и напряжения на зазоре при прохождении сгустка равны
![]() (2.61)
(2.61)
Отрицательный знак в (2.61) указывает на изменение направления тока в результате возврата электронов к резонатору.
Перейдем к комплексным величинам тока и напряжения
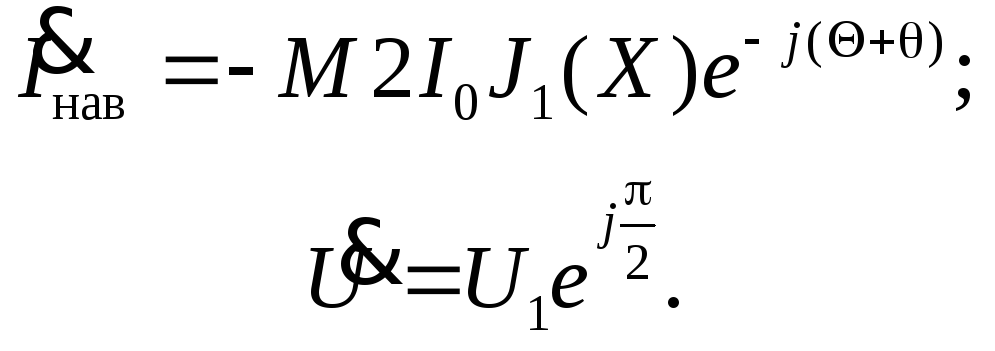 (2.62)
(2.62)
Используя полученные выражения, определим комплексную электронную проводимость зазора
![]() (2.63)
(2.63)
Для удобства дальнейших расчетов выразим амплитуду напряжения U1 через параметр группировки Х. Используя уравнение (2.59), получаем
![]() . (2.64)
. (2.64)
Подставим уравнение (2.64) в (2.63)
![]() (2.65)
(2.65)
где
![]() . (2.66)
. (2.66)
Из (2.65) находим активную и реактивную проводимости Gэл и Bэл
![]() (2.67)
(2.67)
![]() .
(2.68)
.
(2.68)
