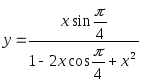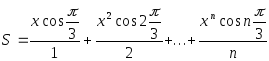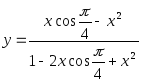Лабораторная работа №4 Вычисление конечных сумм

При решении различных задач мы сталкиваемся с вычислением конечных сумм. При этом, если каждый очередной член суммы отличается от предыдущих и последующих на какую-то заданную величину, то вычисление таких сумм упрощается, поскольку при составлении алгоритма вычисления легко учесть закономерность получения очередного члена.

Сумму конечного числа элементов ряда в общем случае можно записать

.

Обычно при вычислении конечной суммы заранее указывается, сколько раз должно быть произведено суммирование, т.е. задается число N. Вычисление суммы удобно организовать в виде цикла, где увеличение номера очередного члена i на единицу приводит к изменению суммы на величину r_i(x):

Для правильной установки начального значения суммы приi = 1 необходимо положить S₀ = 0. При этом суммирование прекращается при выполнении следующего условия (i > N).

Работа содержит задачи, которые сводятся к нахождению суммы некоторого количества слагаемых

при различных значениях параметра суммирования х. Каждое слагаемое суммы зависит от переменной х и номера n , определяющего место этого слагаемого в сумме.

Обычно формула общего члена суммы принадлежит к одному из следующих трех типов:

1.a) 1.б)1.в).

2.а) 2.б)

2.в)

3.a) 3.б)

3.в)

В случае 1.а), 1.б), 1.в) для вычисления члена суммы целесообразно использовать рекурентные соотношения, т.е. выражать последующий член суммы через предыдущий:

1.а) U₀(x)=1;

U_k(x)=U_k-1(x)_*x/k, k=1,2,3, ... , n.

1.б) U₀(x)=x;

U_k(x)=-(U_k-1(x)_*x²)/((2k)(2k+1)), k=1,2, ..., n.

1.в) U₀(x)=1;

U_k(x)=(U_k-1(x)_*x²)/((2k-1)(2k)), k=1,2, ..., n

В случае 2.а), 2.б) и 2.в) применение рекурентных соотношений нецелесообразно. Вычисления будут наиболее эффективными, если каждый член суммы вычислять по общей формуле.

В случае 3.а), 3.б) и 3.в) член суммы целесообразно представить в виде двух сомножителей:

3.а) U_k(x)=a_n*_k(x); где a_n=1/(4 k+1); _k(x)= x^4k+1

3.б) U_k(x)=a_k*_k(x); где а_k=(-1)^k; _k(x)=coskx/k².

3.в) U_k(x)=a_k*_k(x), где a_k=(k²+1); _k(x)=1/k!(x/2)^k

один из которых:

3.а) U_n(x); 3.б) a_k; 3.в) _k(x).

вычисляется по рекурентному соотношению, а другой:

3.а) а_k; 3.б) _k(x); 3.в) а_k.

вычисляется непосредственно.

Требования к работе

1. Записать расчетные формулы для вычисления слагаемого и суммы.

2. Составить блок схему алгоритма для вычисления заданной суммы в указанном диапазоне изменения параметра х с заданным шагом. Для получения шага диапазон изменения х разделить на 10.

3. Составить программу решения задачи. В программе предусмотреть вычисление суммы соответствующего функционального ряда у по проведенной в таблице формуле.

4. Отладить программу.

Лабораторные задания

N	Сумма	Диапазон изме­нения аргумента	n	Функция
1			10
2			40
3			10
4			40
5			15
6			25
7			10
8			30
9			20
10			10
11	00		35
12			10
13			20
14			30
15			40
16			10
17			50
18			20
19			30
20			40
21			35
22			15
23			40
24
25			20
26			20
27			40
28			40
29			40
30			10