Лабораторные задания

Построить графики следующих функций на отрезке [a, b]

1. a = - 4π, в = 4 π; n = 200.

2. a = - 4π,в = 8; n = 150.

3. ; a = - 8,в = 16; n = 200.

4. ; a = - 4,в = 12π; n = 100.

5. a = - 3,в = 3; n = 500.

6. ; a = - 10, в = 10; n = 100.

7. a = - 20, в = 20; n = 200.

8. ; a = - 10,в = 10; n = 150.

9. a = - 2π,в = 8π; n = 200.

10. a = - 20π,в = 20; n = 200.

11. a = - 5π,в = 5π; n = 150.

12. a = -0;в = 2π; n = 50.

13. a = - 5,в = 10; n = 100.

14. a = - 5π,в = 10; n = 100.

15. a = - 5,в = 10; n = 100.

Лабораторная работа №14 Численное моделирование движения планет вокруг Солнца

Законы движения планет имеют особое значение в развитии науки, поскольку в прошлом они сыграли важную роль в формировании механистического взгляда на Вселенную. Немногие теории оказали столь же огромное влияние на западную цивилизацию, как ньютоновы законы движения и всемирного тяготения, связывающие в единое целое движение звезд и земных объектов. Большую часть наших знаний о движении планет объединили в себе законы Кеплера, которые можно сформулировать следующим образом:

1. Все планеты движутся по эллиптическим орбитам, в одном из фокусов которой находится Солнце.

2. Секторная скорость каждой планеты относительно Солнца постоянна.

3. Отношение квадратов периодов обращения планет к кубам больших полуосей их орбит постоянно и для всех планет одинаково.

Эти законы были установлены Кеплером в результате обработки и анализа данных наблюдений за движением планет, которые на протяжении многих лет были собраны астрономами. Отметим, что первый и третий законы Кеплера касаются формы орбиты, а не зависимости скорости и координаты планеты от времени. Поскольку эти временные зависимости невозможно выразить через элементарные функции, мы в этой работе рассмотрим численное решение уравнений движения планет и их спутников по орбитам.

Движение Солнца и планеты вокруг него является примером задачи двух тел. Эту задачу можно свести к задаче одного тела двумя методами. В основе самого простого метода лежит тот факт, что масса Солнца во много раз больше массы планеты. Следовательно, с хорошей точностью можно считать Солнце неподвижным и связать с ним начало системы координат. Существует и более общий метод, связанный с понятием приведенной массы. А именно, движение двух тел с массами m и М, полная потенциальная энергия которых зависит только от расстояния между ними, можно свести к эквивалентной задаче о движении одного тела приведенной массы , определяемой формулой

(14.1)

Поскольку масса Земли m=5.99*10²⁴ кг, а масса Солнца М=1.9910³⁰кг, то понятно, что для большинства практических целей приведенная масса Солнца и Земли можно взять равной массе Земли. Поэтому ниже мы рассмотрим только задачу об одной материальной точке массы m, движущейся вокруг неподвижного силового центра, который мы примем за начало системы координат.

Как мы уже знаем закон всемирного тяготения Ньютона утверждает, что частица массой М притягивает другую частицу массой m с силой

(14.2)

где вектор направлен от тела с массой М к телу с массой m, a G •- постоянная тяготения, которая равна G=6.67ּ10^-11 m³ /kгּc². У силы тяготения имеются два свойства общего характера: ее величина зависит только от расстояния между телами, а направление совпадает с линией, их соединяющей. Такие силы называются центральными. Из предположения центральности силы следует, что орбита Земли лежит на плоскости (х, у), а угловой момент L сохраняется и направлен по третьей оси (z).

(14.3)

Кроме того, движение ограничивается условием сохранения полной энергии Е, равной

(14.4)

Если связать систему координат с телом массой М, то уравнение движения принимает вид

(14.5)

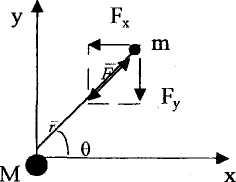
Рис.14.1. Тело массой m движется под действием центральной

силы F.

Для целей численного моделирования удобно записать силу в декартовых координатах. Используя выражения и

напишем

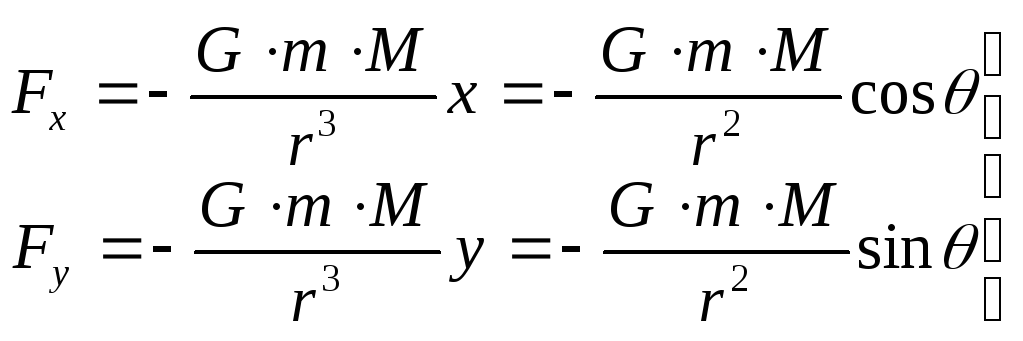(14.6)

В результате уравнения движения в декартовых координатах принимают вид

(14.7)

где r²=х²+у². Уравнение (14.7) есть система дифференциальных уравнений

2-го порядка.

Поскольку большинство орбит мало отличаются от круговых, сначала получим условия движения тел по круговой орбите. Величина ускорения связана с радиусом круговой орбиты r и скоростью соотношением

а =(14.8)

Ускорение всегда направлено к центру и обусловлено гравитационной силой. Следовательно, имеем

(14.9)

или (14.10)

Выражение (14.10), связывающее радиус и скорость, и есть общее условие любой круговой орбиты. Можно также найти зависимость периода Т от радиуса круговой орбиты. Известно, что

Т =

Используя выражение (14.10), получим

(14.11)

Формула (14.11) представляет собой частный случай третьего закона Кеплера, поскольку радиус r соответствует большой полуоси эллипса.

Наиболее общим видом орбиты является эллипс, поэтому опишем и свойства эллиптической орбиты. У эллипса имеются две неравные взаимно перпендикулярные оси. Более длинная ось называется большой осью, короткая ось называется малой осью эллипса, а - есть большая, a b - малая полуоси эллипса соответственно.

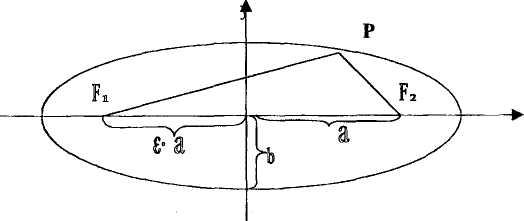
Рис.14.2. Эллипс.

F₁ и F₂ называются фокусами эллипса, и они обладают тем свойством, что для любой точки Р, лежащей на этой кривой, сумма расстояний от фокусов F₁P+F₂P=2a постоянна.

В астрономии принято задавать эллиптическую орбиту величиной а и эксцентриситетом ε, который равен отношению расстояния между фокусами к длине большой оси

причем 0<<1. В частном случаеb=а эллипс превращается в окружность и ε=0. Для орбиты Земли ε =0.0167.

Поскольку работать на компьютере с очень малыми или очень большими числами неудобно, в данной работе желательно выбрать такую систему единиц, в которой величина произведения GM была бы порядка единицы. Для описания движения Земли принято в качестве единицы длины выбирать большую полуось земной орбиты. Эта единица длины называется астрономической единицей (а.е.), она равна

1а.е.= 1.496ּ10¹¹ м. В качестве единицы времени принимается

один год=3.15ּ10¹⁷с. В этих единицах Т=1год и а=1 а.е. можно записать

Для моделирования задачи Кеплера необходимо использовать алгоритм, Эйлера-Кромера и решить систему уравнений движения (14.7) численно с помощью этого алгоритма. В работе необходимо использовать три одномерных массива, содержащих по два элемента, каждый представляет соответственно координату, скорость и ускорение тела.

Упражнения

1 Составьте программу для вычисления значений координаты и скорости и для построения графика орбиты планет. Проверьте правильность программы, рассматривая частный случай круговой орбиты. В качестве примера возьмите (в а.е.) х₀=1,у_о=0 и u_х(t=0)=0. С помощью соотношения (14.10) найдите численное значение u_y(t=0), которое дает круговую орбиту. Выберите значение шага t таким образом, чтобы полная энергия Е сохранялась с хорошей точностью.

2. Пропустите программу с различными значениями начальных условий х₀ и u_y(t=0)=0, соответствующими условиям круговой орбиты. Задайте у_о=0 и u_x(t=0)=0. Для каждой орбиты определите радиус и период и проверьте правильность третьего закона Кеплера

3. Задайте y_o=0 и u_x(t=0)=0. Методом проб и ошибок подберите несколько вариантов значений х₀ и u_y(t=0), которые приводят к эллиптическим орбитам. Для каждой орбиты определите полную энергию, угловой момент, большую и малую полуоси, эксцентриситет и период обращения.

4. Модифицируйте свою программу гак, чтобы она рисовала траекторию движения планеты. Получите на мониторе орбиту вращения и покажите, как меняется орбита при изменении начальных условий.