
- •Оглавление
- •Задание
- •Лабораторная работа №2 Создание и заполнение таблиц в табличном процессоре Excel 97
- •Задание 1
- •Задание 2
- •Изменение выбранного эффекта
- •Просмотр выбранных эффектов анимации
- •Удаление выбранных эффектов анимации
- •Лабораторная работа №3 Вычисление сложных выражений
- •Лабораторная работа №4 Вычисление конечных сумм
- •Требования к работе
- •Лабораторные задания
- •Лабораторная работа №5 Вычисление определенных интегралов и табулирование первообразных функций
- •Лабораторная работа № 6 Вычисление бесконечных сумм
- •Лабораторная работа № 7 Обработка и преобразование числовых последовательностей
- •Лабораторная работа № 8 Вложенные циклы с разветвлениями. Использование массивов.
- •Лабораторные задания
- •Лабораторная работа № 9 Использование подпрограмм при программировании на языке Паскаль
- •Лабораторные задания
- •Лабораторная работа № 10
- •Лабораторные задания
- •Лабораторная работа №11 Операции над файлами
- •Лабораторные задания
- •Лабораторная работа №12 Простейшие графические построения
- •Простейшие процедуры
- •Константы цвета
- •Требования к работе
- •Лабораторные задания
- •Лабораторная работа №14 Численное моделирование движения планет вокруг Солнца
- •Лабораторная работа №15 Моделирование поведения линейных и нелинейных колебательных систем
- •Упражнения
- •Лабораторная работа №16 Вычисление электрического и магнитного полей создаваемых стационарным распределением зарядов и токов
- •Литература
Лабораторная работа №15 Моделирование поведения линейных и нелинейных колебательных систем
Во многих физических системах движение носит регулярный периодический характер. Движение, которое повторяется через конечный интервал времени, например, движение Земли вокруг Солнца, называют периодическим. А любое периодически повторяющееся движение называется колебанием. Примерами колебаний, с которыми мы встречаемся в повседневной жизни, служат маятник в часах и звучащая струна гитары. Менее очевидными примерами являются микроскопические явления, такие как колебания атомов в кристаллах.
Для ознакомления с основными понятиями, связанными с простыми колебаниями, рассмотрим тело массой т, прикрепленное к свободному концу пружины (рис.15.1). Тело скользит по горизонтальной поверхности без трения. Будем задавать положение тела координатой х и примем точку х=0 в качестве положения равновесия, т. е. положения в котором пружина ненапряжена. Если тело сместить из положения равновесия х=0 и затем отпустить, то оно будет колебаться в горизонтальном направлении. Известно, что если пружина не слишком сильно растянута или сжата, то сила, действующая на тело с координатой х, является линейной относительно х
:
F =-кх. (15.1)
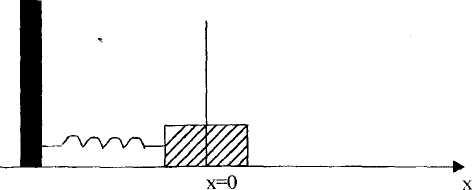
Рис.15.1. Пример одномерного простого гармонического осциллятора
Силовая постоянная к является мерой жесткости пружины. Знак минус в (15.1) указывает на то, что сила стремится вернуть тело в положение равновесия. Уравнение движения этого тела можно записать в виде
![]() (15.2)
(15.2)
где
![]() .
Уравнение
(15.2) есть пример линейного дифференциального
уравнения второго порядка. Движение,
описываемое уравнением (15.2) называется
простым гармоническим колебанием, и
его решение можно выразить аналитически
через синусы и косинусы. Приведем здесь
решение этого уравнения. Одно из решений
имеет вид
.
Уравнение
(15.2) есть пример линейного дифференциального
уравнения второго порядка. Движение,
описываемое уравнением (15.2) называется
простым гармоническим колебанием, и
его решение можно выразить аналитически
через синусы и косинусы. Приведем здесь
решение этого уравнения. Одно из решений
имеет вид
![]() ,
(15.3)
,
(15.3)
где
а
и
![]() - постоянные, а аргумент косинуса
выражается в радианах. Постоянныеа
и
- постоянные, а аргумент косинуса
выражается в радианах. Постоянныеа
и
![]() называются амплитудой и начальной фазой
и могут быть определены из начальных
условий для координатых
и скорости
называются амплитудой и начальной фазой
и могут быть определены из начальных
условий для координатых
и скорости
![]() =
dx/dt.
Поскольку
косинус является периодической функцией
с периодом 2
=
dx/dt.
Поскольку
косинус является периодической функцией
с периодом 2![]() ,
то функцияx(t)
в выражении
(15.3) также периодическая. Определим
период Т как наименьшее время, через
которое движение повторяется, т.е.
,
то функцияx(t)
в выражении
(15.3) также периодическая. Определим
период Т как наименьшее время, через
которое движение повторяется, т.е.
x{t + T)=x{t).
Поскольку
![]() Т
соответствует
одному периоду, получим
Т
соответствует
одному периоду, получим
![]() (15.4)
(15.4)
Частота
колебаний
![]() представляет собой число периодов в
секунду и определяется выражением
представляет собой число периодов в
секунду и определяется выражением![]() .
Заметим, что
Т зависит от отношения к/т
и не зависит
от а и
.
Заметим, что
Т зависит от отношения к/т
и не зависит
от а и
![]() .
Следовательно, период простых гармонических
колебаний не зависит от их амплитуды.
Хотя координата и скорость осциллятора
непрерывно изменяются, полная энергия
Е остается постоянной и равна
.
Следовательно, период простых гармонических
колебаний не зависит от их амплитуды.
Хотя координата и скорость осциллятора
непрерывно изменяются, полная энергия
Е остается постоянной и равна
![]() (15.5)
(15.5)
Эти два члена в формуле (15.5) можно отождествить соответственно с кинетической и потенциальной энергией.
Другим общеизвестным примером колебательной механической системы является «математический» маятник. Уравнение движения для маятника имеет следующий вид
ml![]() или
или
![]() ,
(15.6)
,
(15.6)
где
l
длина,
а
![]() угол отклонения маятника. Уравнение
(15.6) является примером нелинейного
дифференциального уравнения. Большинство
нелинейных уравнений не имеют аналитических
решений и (15.6) не является исключением.
Однако, если амплитуда колебаний маятника
достаточно мала,
то можно предположить sin
угол отклонения маятника. Уравнение
(15.6) является примером нелинейного
дифференциального уравнения. Большинство
нелинейных уравнений не имеют аналитических
решений и (15.6) не является исключением.
Однако, если амплитуда колебаний маятника
достаточно мала,
то можно предположить sin![]() и
(15.6) переписать в виде
и
(15.6) переписать в виде
![]() (15.7)
(15.7)
для
![]() 1.
Если сравнить уравнения (15.2) и (15.7) и
сопоставить переменные
х и
1.
Если сравнить уравнения (15.2) и (15.7) и
сопоставить переменные
х и
![]() ,
то видно, что эти два уравнения имеют
одинаковый вид и следовательно они
будут иметь одинаковое решение.
Отсюда
можно сделать сразу вывод, что для
,
то видно, что эти два уравнения имеют
одинаковый вид и следовательно они
будут иметь одинаковое решение.
Отсюда
можно сделать сразу вывод, что для
![]() «1 период математического маятника
равен
«1 период математического маятника
равен
T=2![]()
![]() (15.8)
(15.8)
В случае больших амплитуд колебаний для получения представления о движении маятника необходимо численно решить уравнение (15.6). Поскольку мы знаем, что численное решение должно удовлетворять условию сохранения полной энергии, то напишем выражение для нее в явном виде
E=![]() (15.9)
(15.9)
Первый и второй члены в выражении (15.9) представляют собой кинетическую и потенциальную энергии соответственно.
Известно, что в природе большинство колебаний постепенно уменьшается до тех пор, пока смещение не становится нулевым. Такие колебания называются затухающими. В качестве примера гармонического осциллятора с затуханием рассмотрим движение грузика с учетом горизонтальной тормозящей силы. Для движения с малыми скоростями в качестве приближения разумно принять, что тормозящая сила пропорциональна первой степени скорости. В этом случае уравнение движения можно записать в виде
![]()
![]()
![]() (15.10)
(15.10)
где коэффициент у представляет меру тормозящей силы.
Далее остановимся на рассмотрении колебаний, которые имеют место в электрических цепях. Отправной точкой в теории электрических цепей является закон Кирхгофа, который гласит, что сумма падений напряжения на участках замкнутой цепи равна нулю. Этот закон является следствием сохранения энергии, которая теряется или приобретается в процессе прохождения единичного заряда через элементы цепи. Представим себе электрическую цепь, состоящую из источника переменного напряжения и соединенных последовательно резистора, индуктивности и конденсатора (рис.15.2). Падение напряжения на каждом элементе цепи определяется с помощью следующих формул:
VR=IR;
Vc=![]() ;
V
;
V![]()
![]() ;
(15.11)
;
(15.11)
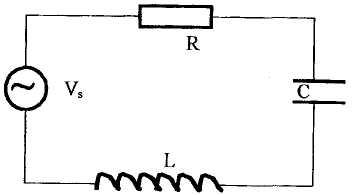
Рис.15.2. Простая последовательная RLC-цепь с источником напряжения Vs.
Соответствующее этой цепи общее уравнение имеет вид:
VL+VR+VC=VS, (15.12) где Vs есть ЭДС источника. Подставляя (15.11) в (15.12), получим
![]() (15.13)
(15.13)
где
![]()
Q – заряд (в кулонах); R- сопротивление (Омы); С- емкость (в фарарах); L – индуктивность (в генри).
Видно, что вид уравнения (15.13) для последовательной RLC -цепи совпадает с уравнением (15.10) для гармонического осциллятора с затуханием.
Теперь перейдем к моделированию и численному решению приведенных выше уравнений. Поскольку уравнения (15.10) и (15.13) имеют одинаковый вид, достаточно решить одно из этих уравнений. Для моделирования колебаний хорошо подходит уже известный нам алгоритм Эйлера - Кромера. В программе с помощью алгоритма Эйлера - Кромера необходимо вычислить зависимости координаты и скорости простого гармонического осциллятора от времени. Результаты вычислений необходимо вывести на экран. Сначала необходимо убедиться в том, что при надлежащем выборе шага Аt, алгоритм Эйлера - Кромера можно использовать для описания движения простого гармонического осциллятора. Поскольку нам известно аналитическое решение уравнения (15.2) для этого случая, то одно из условий выбора значений At заключается в том, что вычисленные значения должны соответствовать аналитическим результатам (15.3). Более общим условием правильности выбора значения At, не связанным с существованием аналитического решения, является условие сохранения полной энергии.
