24. Теплоемк тв. Тел. Модели Эйнштейна и Дебая.

ТТ состоит из частиц, закрепленных в узлах. А в кристаллическом ТТ частицы расположены в узлах упорядоченно. Под действием тепловой энергии атомы совершают гармонические колебания около положения равновесия. Следовательно эти атомы обладают кинетической и потенциальной энергиями (m v²)/2=кТ/2; U=кТ/2. Тогда на 1 степень свободы приходится энергия атома кТ. И внутренняя энергия 1 атома =3кТ. Внутр. Энергия 1 моля = U_μ = 3 N_AкТ = RT. Теплоемкость при пост. объеме C_v = dU/dT=3R для ТТ: C_{V TT} =3R впервые было сказано Дюлонгом и Пти (1819). Теплоемкость 1 моля любого атомарного ТТ = 3R. Если в узлах решетки находятся не атомы, а молекулы, то Джоуль и Конн распространили закон Дюлонга и Пти и на этот случай. C_v=3nR, где n – число атомов в молекуле. Теплоемкость одного моля ТТ для всех одинакова и не зависит от темп-ры. Однако, теплемк. ТТ , по эксп-м данным, зависит от темп-ры. Исходя из законов кв. мех. Дебай объяснил эту зависимость след. обр.: атомы в узлах решетки совершают колебания. При низких темп-рах они совершают колебания и имеют энергию hν, ν - частота. При Т→0К теплемк. по Дебаю C_V~Т³ т.е. уменьшается по кубическому закону с уменьшением

темп-ры.Этот закон наз. Законом кубов Дебая. С ростом темп-ры частота колебаний увеличивается, увел-ся энергия hν, но не беспредельно, т.е. до Т = θ, наз. Т Дебая. Эйнштейн разработал свою модель зав-ти теплоемкости ТТ от темп-ры. Он нашел, что:

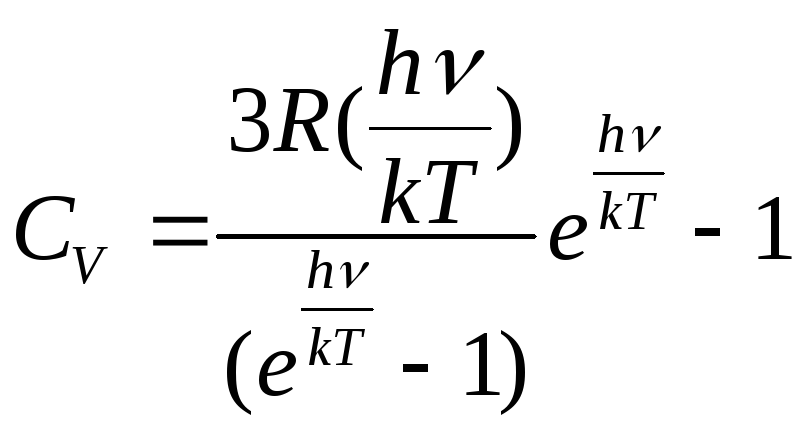
При Т→0, C_V→0; При Т→∞, C_V→3R.

25. Теория флуктуаций. Броуновское движение. Хотя физич-е величины определяющие макроскопическое тело с большой точностью равны своим средним значениям, они флуктуируют (отклоняются от своего ср.знач-я). Рассмотрим замкнутую систему и обозначим через x некоторую физич-ю величину характеризующую систему или ее часть. Будем полагать что, что <x> уже вычтено из x и предположим что <x> = 0. Вероятность ρ(x) = const exp(S(x)). Здесь S(x) - энтропия рассматриваемая как ф-ция точных значений х. Энтропия = Мах, при равновесном состоянии системы. При х = <x> = 0, S = S_max. Но в точке Мах. 1-я производная = 0. (∂S/∂x)_x=0 = 0, (∂²S/∂x²)_x=0 < 0. В точке Min (∂²S/∂x²)_x=0 > 0. Разложим энтропию по степеням малого параметра х. S(x) = S(0) + x(∂S/∂x)_x=0 + x²(∂²S/∂x²)_x=0 + … = S(0) – βx²/2 + …, (β>0) и тогда ρ(x) = const exp(S(0)) exp(-βx²/2) = A exp(-βx²/2); А находим из условия нормировки:

1 = ∫ρ(x)dx = A∫ exp(-βx²/2)dx = A√(2π/β),

A = √(β/2π) и ρ(x) = √(β/2π) exp(-βx²/2) (1) ρ(x)dx – вероятность того, что х примет значения от х до x+xdx.

1. – Распределене Гаусса.

<x²> = ∫x²ρ(x)dx = √(β/2π) ∫x²exp(-βx²/2)dx,{βx²/2 = y,

x = √(2y/β),dx = 1/2√(y ^-1/2)dy} <x²> = √(β/2π) 2/β ∫ y exp(-y)1/2 √(2/β)y ^-1/2 dy = 1/√(2π) (√2)/β ∫(-∞, +∞) exp(-y)y ^-1/2 dy = 1/(β√π) 2Г(3/2) = (√π)/2 2/√(πβ) = 1/β (2)

(1) → (2) ρ(x)dx = √(1/2π<x²>) exp(-x²/2<x²>)dx.

Известно что ∆S_n – изменение энтропии.

∆S_n = - R_min/T = - (∆E - T∆S + P∆V)/T , тогда

ρ ~ exp(-R_min/T) = exp(- (∆E - T∆S + P∆V)/T);

R- работа, ∆E, ∆S, ∆V- изменение энергии энтропии и объема при флуктуациях. В таком виде ф-ла (3) применима к любым флуктуациям.

Если мы запишем

∆E(S,V) = (∂E/∂V)_V∆S + (∂E/∂V)_E∆V + 1/2((∂²E/∂S²)(∆S)² + (∂²E/∂V²)(∆V)²) + 2 (∂²E/∂S∂V)(∆S∆V)) (4);

dE=TdS-PdV;

T = (∂E/∂S)_V,

P = - (∂E/∂V)_S.

Когда подставляем (4) в (3) то 2 члена уничтожаются и

∆E - T∆S + P∆V = 1/2((∂²E/∂S²)(∆S)² + (∂²E/∂V²)(∆V)²) + 2 (∂²E/∂S∂V)(∆S∆V)) = 1/2 (∆S∆(∂E/∂S)_V + (∆V∆(∂E/∂V)_S) = 1/2 (∆S∆T - ∆V∆P).

Тогда ρ ≈ exp(-(∆T∆S + ∆P∆V)/2T) - для конкретных ТД флуктуаций. Броуновское движение- это движение взвешенных частиц в жидкости или в газе, которые сов-ют хаотические движения в связи со столкновениями с частицами рассматриваемой среды.

26. Реальные газы. Уравнение Ван-дер-Ваальса. Поведение реальных газов хорошо описывается уравнен. pV=RT (1) только при малых плотностях, то есть при не слишком больших давлениях и достаточно высоких температурах. С повышением давления и понижением температуры наблюдаются значительные отступления от этого ур-я. Для описания поведения газов в широком интервале плотностей было предложено много различных уравнений. Самым простым из них и вместе с тем дающим достаточно хорошие результаты оказалось уравнение Ван-дер-Ваальса. Это уравнение получено путем введения поправок в ур. (1) и имеет след. вид (p + a/V²)(V - b) = RT (2) где p – давление, оказываемое на газ извне (равно давлению газа на стенки сосуда), a и b – константы Ван-дер-Ваальса, имеющие для различных газов различные значения, определяемые опытным путем. Если давление выражено в паскалях, а объем в кубических метрах на киломоль, то константа а изм. в Па*м6/кмоль2, а константа b – в м3/кмоль. Из-за взаимного притяжения между молекулами газ как бы сжимается большим давлением, чем p, оказываемое на газ стенками сосуда, в котором он заключен. Поправка a/V2 характеризует ту добавку к внешнему давлению, которая обусловлена взаимным притяжением молекул друг к другу. Заметное воздействие молекул друг на друга осуществляется в пределах небольших расстояний, наз. радиусом молекулярного действия. Вследствие того, что молекулы обладают конечным объемом, пространство, доступное для движения молекул, оказывается меньшим, чем объем сосуда V. Поправка b характеризует ту часть объема, которая недоступна для движения молекул. Она равна по порядку величины нескольким суммарным объемам молекул, содержащихся в киломоле газа. Реальные газы следуют ур. Ван-дер-Ваальса лишь приближенно. Воображаемый газ точно подчиняющийся ур. (1) наз. Ван-дер-ваальсовским. Внутренняя энергия ван-дер-ваальсовского газа должна включать в себя, кроме кинетической энергии молекул, энергию взаимодействия между молекулами: U = C_vT – a/V Ур. ВДВ из стат. физики: (P + N²a/V²)(V - Nb) = NT

27. Жидкости. Поверхностные явления. Мол-лы жидк. обладают потенциальной и кинет. энергией. Внутри жидк. каждая мол-ла со всех сторон окружена такими же мол-ми и взаимод с ними в пределах молекулярной сферы., поэтому можно считать, что равнодействующая всех сил равна нулю. Если мол-лы нах-ся на поверхности, то мол-я сфера погружена только половиной в жидк. и равнод. всех сил, приложенная к мол-ле будет направлена перпендик. к поверхности в объем. Под действием этой силы мол-ла может перейти с поверхности в объем, совершая при этом положит работу. А для поднятия мол-лы на поверхность нужно совершить отр. работу по преодолению этой силы. Переход мол-лы не поверхность означает увелич. площади пов-ти, а энергия на поверхности больше, чем в объеме, тогда dU~dS, т.е.изменение пов-й энергии будет пропорц. площади пов-ти: dU=σdS, где σ- коэ-т пропорц., зависящий от св-в жидк. σ=dU/dS-поверхн. энергия, приход на ед. площади(плотность поверх-й энергии). При переводе мол-лы на пов-ть ее потенц энергия увелич, след-но меняется расст между мол-ми и расст. между мол-ми на поверхн. уменьш. и на поверхн. образуется уплотненный слой. Этот поверхн. слой можно натянуть, поэтому между мол-ми пов-ти возник сила поверхн. натяж. С.п.н. лежит в плоск-и пов-ти или если пл-ть кривая, то совпадает с касат в данной т. а само явление наз-ся поверх-м натяжением. С.п.н. и равнод. R направлены перпендик. пов-ти в объем. R старается переместить мол-лу в объем, а с.п.н. удержать мол-лу на пов-ти поэтому устойчивая пов-ть образуется при равнодействии этих сил. Т.О. с.п.н.: действует на каждую мол-лу пов-ти; действует по всему направлению пов-ти; величины этих сил равны между собой; совершает работу. dA=Fнdx=dU, dU=σdS, P=Fн/S => Fн=PS; S=Ldx, тогда dA=dU=σdS=σLdx.

Т.О. коэф-т пов-й энергии σ=F/L-это есть силовой смысл. [σ]=[н/м]. Коэ-т пов. натяж. не зависит от размеров площади пленки и в зависимости от природы меняется от 1/10 до 1/1000 н/м. На форму жидк. влияет с.п.н., сила тяжести и взаимод жидк. с мол-ми соприкос. сред. Давление оказ. искривленной пов-ю на ниже леж. слои: P=2σ/r. Сущ-ют жидк. кот смачиваются и несмачиваются. Если жидк. смачив. тв. тело, то она растик по пов-ти, если частично смачив. то образуется капля, если жидк. несмачив., то она образует сплющенную каплю. Если жидк. смачив, то она поднимится по стенкам сосуда, если жидк несмачив., то опустится по краям. При этом появляется дополнительная сила, увелич или уменьш. силу Архимеда. Эти силы отн. невелики. В зависим. от смачив. жидк. она подним или опускается в капиллярах (тонких трубках). Если капилляр опустить в смач. жидк. то она подним. и принимает вогн. форму. Высота подъема жидк. при этом опред. по ф-ле: L=2σ·cosθ/Rgρ, где r- радиус кривизны пов-ти, R-радиус кривизны капилляра.

28. Твердые тела. Кристаллы. Симметрия кристаллов. Твердые тела делятся на аморфные и кристаллические тела. Аморфные тела с одной стороны обладают свойствами твердых тел (стекло), т.е. сохраняют объемы формул. С другой стороны, обладают свойствами жидкости с большой вязкостью. Например: стекло, смола при низких температурах, являются твердыми веществами. С увеличением температуры стекло и смола размягчаются, вязкость уменьшается. Аморфные тела можно рассмотреть как жидкость с большой вязкостью. В отличие от аморфных тел, кристаллические тела при нагревании плавятся при определенной температуре. Следовательно, это говорит о различии во внутреннем строении кристаллических и твердых аморфных тел. В аморфных твердых телах имеется ближний порядок атомов, молекул. Кристаллические тела имеют определенную температуру плавления. Кроме того, свойства кристаллических тел обладают анизотропией, т.е. они зависят от направления свойств. Это говорит о том, что кристаллические тела имеют особое внутреннее строение. В кристаллическом теле направлены упорядоченно, в одном направлении. Если мы сломаем кристалл, то он будет ломаться там, где расстояние между атомами больше. В результате этого, образуется внешняя структура. Симметрия кристаллов. Т.к. кристаллы – это правильное строение, то они обладают симметрией расположенных частей.

Симметрией называется способность тела повторять свои равные части путем особых преобразований, называемых симметриями преобразования. Из-за большого числа кристаллов можно ожидать, что симметричных преобразований также будет много. Однако существует 4 системы преобразований для внешней формы кристалла: 1. вращение вокруг осей симметрии и соответственно этой операции элемент симметрии ось симметрии. 2. отражение в плоскости симметрии. 3. отражение в центре симметрии (инверсия) элемент симметрии – точка симметрии. 4. зеркально поворотная ось симметрии.

29. Фазовые переходы 1и 2-го рода. Различают прерывные и непрерывные фп. Прерывными называются фп, при кот-х первые производные от G: V=(G/р)_т , S=-(G/Т), испытывают скачки, а непрерывными - фп, при кот-х первые произ­водные непрерывны, а терпят разрыв производные второго и более высоких порядков: теплоемкость С_р=- Т(  ²G/Т²)_р, сжимаемость _т=-1/V*( ²G/р²)_т, коэффициент теплового расширения =1/V ((  ²G/Тр) и т. д. Прерывные превращения наз-ся фп первого рода. Фп первого рода являются плавление, кристаллизация, кипение, некоторые превращения из одной кристаллической модификации в другую, переход проводника в сверхпроводящее состояние в маг поле и т. д. Непр-ные переходы, при которых 2е производные от энергии Гиббса (или химического потенциала) испытывают скачки, наз-ся фп второго рода, Основ ур-ем, характеризующим фп 1-го рода, яв-ся дифф ур-е Клапей­рона-Клаузиуса (КК). Это ур-е получ-ся из условия рав-ва хим потенциалов при равновесии двух фаз '(р, Т)="(р, Т) (1) и связывает между собой теплоту перехода, скачок удельного объема и наклон кривой равновесия в точке перехода. Дифф-уя (1), получаем d’(р,Т)= d’’ (р,Т) или

(∂’/∂T)_pdT + (∂’/∂P)_TdP = (∂’’/∂T)_pdT + (∂’’/∂P)_TdP,

откуда dP/dT = ((∂’’/∂T)_p - (∂’/∂T)_p)/( (∂’/∂P)_T - (∂’’/∂P)_T),

dP/dT = (s’’ – s’)/(v’’ – v’) (3)

т к d= - sdT+dp (s и υ— энтропия и объем на 1 ч-цу). Ур-е (3) яв-ся диф ур-ем кривой равн-сия и наз-ся ур-ем КК. Чаще его запис в виде

dP/dT = λ/(T(v’’ – v’)) (4)

где λ=T(s"—s') - теплота перехода на моль или грамм в-ва; v’’ – v’ - изм-е объема соответ массы в-ва.

Условие устойчивости и равновесия. Рассмотрим замкнутую систему в термостате с температурой Т и под давлением P. Общим условием устойчивости такой системы является минимум ее энергии Гиббса.

Ф = E – TS –PV. Cостояние системы в термостате при данных Т и P с экстенсивными параметрами V, S является устойчивой, если энергия Гиббса увеличивается при небольшом спонтанном изменении этих параметров.

∆Ф = Ф₁ – Ф>0.

E₁ – E = T(S₁ - S) + P(V₁ - V) (1), Е – внутренняя энергия исходного равновесного состояния при P и Т с координатами V,S. Е1 – внутренняя энергия при неравновесном состоянии равная ее равновесному значению при координатах V1,S1, и других обобщенных силах Т1, P1. Аналогично равновесное состояние системы с координатами V1,S1 при постоянных P1 и Т1 будет устойчивым, если при небольшом спонтанном изменении этих параметров выполняется следующее условие:

E – E₁ – T₁(S – S₁) + P₁(V – V₁)>0 (2).

Если сложить (1) и (2), получится: (T – T₁)(S – S₁) + (P – P₁)(V₁ - V)>0.

Если это выражение переписать в виде определителя, то получим матрицу устойчивости.

30. Явление переноса. В термодинамической неравновесной системе возникают особые неравновесные процессы, называемые явлением переноса, в результате которых происходит перенос в пространстве энергии, массы и импульса. К явлениям переноса относятся: 1) теплопроводность (перенос энергии); 2) диффузия (перенос массы); 3) внутренние трение или вязкость (перенос импульса);

1. Теплопроводность. Если в некоторой области газа средняя кинетическая энергия молекул больше, чем в остальных областях, то за счет хаотического движения молекул и соударений между ними происходит постоянное вырабатывание кинетической энергии молекул по всему объему газа. Энергия переносится из областей, где температура газа выше в те области, где она ниже. Рассмотрим одномерный случай: если T1 > T, то dQ = - χ (dT / dx) S dt; χ = 1/3 cp<v> <λ>; c – теплоемкость, p – плотность.

2. Диффузия – это обусловленное тепловым движением выравнивание концентрации смеси нескольких веществ. Этот процесс наблюдается в газах, жидкостях и твердых телах. Рассмотрим двухкомпонентную смесь. Будем считать, что молекулы обеих компонент обладают близкими массами и близкими значениями эффективных диаметров. В этом случае можно считать, что <v> и <λ> у молекул обеих компонент одинаковы. Эмпирическое уравнение диффузии имеет вид: dm_i =Д (dp_i / dx) dS dt. Д – коэффициент диффузии. Д = 1/3 <v> <λ>; dp_i/dx – градиент плотности; Т.к. <v> и <λ> для обеих компонент смеси примерно одинаковы, то и коэффициент диффузии для них будет одинаков.

3. Вязкость или внутреннее трение. В потоке газа мол-лы участвуют одновр в двух видах дв-й – хаотическом тепловом и упорядоченном направленном дв-ии. Пусть <v> - скорость хаотич тепл-го дв-я, а <u> - скор упорядоч дв-я м-л; u<<v; В рез-те дв-я мол-л, мол-лы из слоя газа, дв-ся с одной поступат скор u будут перемешиваться с мол-ми из др. слоя. В рез-те столкновения мол-л м/у собой мол-лы из быстрого слоя будут передавать часть своего импульса мол-лам из медленного слоя и таким образом тормозиться. По этой причине в газе возникает сила внутр трения, которая замедляет дв-е быстрых слоев и ускоряет дв-е медленных слоев. F_тр = η | du/dx| S; При увеличении т-ры газа возр скорость теплового дв-я мол-л и частота соударений между ними. Следствием этого является увеличение переноса импульса от одного слоя газа к другому, поэтому при увеличении т-ры газа, его вязкость возр. Иная картина набл-ся в жидкостях. В жидкостях основной причиной возникновения внутр трения являются межмол-ные взаимодействия. С увел т-ры жидкости возр скорость теплового дв-я мол-л и их кинет эн оказывается достаточно для разрыва межмол-х связей. Это приводит к ослаблению взаим-я м/у мол-ми уменьшению вязкости жидкости.

31. Кинетическое уравнение Больцмана. Понятие об Н-теореме. Нам известна теория Лиувилля dρ/dt = 0 - производная ф-ции распределения по времени равна 0. Дифференцирование идет вдоль фазовой траектории, определяемой ур-ями движения.

dρ/dt = ∂ρ/∂t + ∂ρ/∂r ∂r/∂t + ∂ρ/∂P ∂P/∂t ρ(q,p,t) – зависит от обобщенных коор-т, импульса и времени.

dρ/dt = ∂ρ/∂t + υρ + F dρ/dP, когда газ без столкновений. Но в газе между частицами сущ-ет взаимодействие и учитывая это надо в правой части записать выр-е учитывающее это взаимодействие.

dρ/dt = - υρ + F dρ/dP + stρ (2) stρ – интеграл столкновения. (2) – кинетическое Ур-е имеет реальнй смысл, если мы можем определить интеграл столкновения dρ/dt = stρ (2^/)

dГ – Эл-т объема фаз-го пр-ва.

Если столкнуться две частицы, то их Г и Г^/ → Г₁ и Г₁^/ . И надо рассмотреть вероятность столкновений ω(Г^/, Г₁^/; Г, Г₁) , ω^/(Г, Г₁; Г^/, Г₁^/)

ρ, ρ₁, ρ^/, ρ₁^/ - ф-ции распределения для 1 и 2 частиц до и после столкновения.

Интеграл столкновений stρ=∫ω^/(ρ^/ρ₁^/-ρρ₁)d Г₁d Г^/d Г₁^/ Рассматриваем частицы, входящие и выходящие в объем d Г, поэтому не имеем за ∫-м dГ.

ω^/ =ω(Г, Г₁; Г^/, Г₁^/) ω= ω(Г^/, Г₁^/; Г, Г₁).

∫ω(Г^/, Г₁^/; Г, Г₁)d Г^/d Г₁^/= ∫ω^/(Г, Г₁; Г^/, Г₁^/) dГ^/dГ₁^/;

dρ/dt = - υρ - F dρ/dP + ∫ω^/(ρ^/ρ₁^/-ρρ₁)d Г₁d Г^/d Г₁^/ (3)

Ур-е Больцмана. Равновесная ф-ция распределения удовл-ет кинетич-му ур-ю Больцмана тождественно:

dρ/dt = - υρ + F dρ/dP = ∫ω^/(ρ^/ρ₁^/-ρρ₁)d Г₁d Г^/d Г₁^/ ;

ρ=ρ₀ - равновесная ф-ция распределения изотропна и стационарна и в отсутствии внешнего поля однородна.

Т.е. dρ/dt = 0; υρ = 0; F dρ/dP.

Если левая часть равна 0, то тогда правая часть (интеграл столкновения) тоже равна 0. и ρ^/₀ρ^/₀₁= ρ₀ρ₀₁ ;

ρ₀ ~ exp(- ε/T); exp(-(ε + ε₁)/T) = exp(-(ε’ + ε’₁)/T). Равновесная ф-ция распределения удов-ет кинетич. ур-ю и при наличии внешнего поля. И в этом случае правая часть (3) = 0 и левая = 0, потому что эта левая часть есть полная производная от ф-ции распределения по времени, в которой обращается в 0. В связи с тем, что ρ зависит только от интеграла движения. В связи с тем, что этот интеграл дифференц ур-е (3) в таком виде сложно решить, то приходиться перейти к грубой оценке интеграла столкновений. stρ = - (ρ – ρ₀)/τ, τ - время свободного пробега частиц между столкновениями.

Понятие об Н-теореме: Очевидно, что представленный самому себе газ как и всякая замкнутая система стремится прейти в состояние статистического равновесия. Соответственно этому эволюция неравновесной ф-ции распределения ρ согласно кинетическому уравнению Больцмана должна сопровождаться возрастанием энтропии газа. dS<dt≥0. S = ∫ρln(e/ρ)dГdV. Отсюда dS/dt = ∫ d/dt(ρln(e/ρ))dГdV. Надо найти dS/dt и показать что она ≥ 0.