1. Кинематика материальной точки. Под материальной точкой понимается физический объект, в геометрическом смысле эквивалентный математической точке, но обладающий массой. Кинематика – раздел физики, изучающий виды движения тел без рассмотрения причин возникновения движения. Положение точки в пространстве характеризуется радиусом-вектором. Радиусом-вектором точки называется вектор, начало которого совпадает с точкой начала системы координат, а конец – с рассматриваемой точкой. r = ix + jy + kz. Скорость – расстояние, проходимое телом в единицу времени v(t) = dr/dt. v(t) = i dx/dt + j dy/dt + k dz/dt. Ускорение – скорость изменения скорости. a = dv/dt = d²r/ dt² = i d²x/dt² + j d²y/dt² + k d²z/dt². a = a_τ + a_n = τ dv/dt + n v² /R.

dr = v dt; dv = a dt, следовательно v = v₀ + at; r = r₂ – r₁ = v₀t + at² /2.

2. Динамика материальной точки. Законы Ньютона. Основными понятиями в динамике являются понятие о массе и силе. Сила – это есть причина движения, т.е. под действием силы тела обретают скорости. Сила есть величина векторная. Масса – мера инертности тела. Произведение массы на скорость называется импульсом p = mv. Моментом импульса материальной точки называется вектор L = r * p. Моментом силы, действующей на материальную точку, называется вектор M = r * F. Если продифференцировать выражение для момента импульса, то получим: dL / dt = dr / dt * p + r * dp / dt. Учтя, что dr / dt = v и v параллельно p, получим dL / dt = M. Законы Ньютона. Первый закон Ньютона гласит, что тело, сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие силы или их действие скомпенсировано. Второй закон Ньютона гласит, что изменение количества движения по времени, это есть величина постоянная и равна действующей силе dp / dt = d / dt (mv) = m dv / dt = F. Это и есть второй закон Ньютона, записанный в дифференциальном виде. Третий закон Ньютона говорит о том, что во взаимодействии двух тел каждое из них действует на другое с одинаковой по значению, но противоположной по направлению силой. F₁ = - F₂.

3. Динамика системы материальных точек. Законы сохранения. Системой материальных точек называется совокупность конечного их числа. На каждую из точек системы действуют внутренние (со стороны других точек) и внешние силы. Пусть m – масса, r_i – радиус вектор. x_i, y_i, z_i­ – корд. i-ой точки. Импульсом системы материальных точек называется сумма импульсов материальных точек, составляющих систему: p = Σ (i=1,n) p_i = [p₁ + p₂ +…+ p_n]. Моментом импульса системы материальных точек называется сумма моментов импульса, составляющих систему материальных точек: L = Σ [L_i] = Σ [r_i * p_i]. Сила, действующая на систему материальных точек, определяется как сумма всех сил, действующих на точки системы, включая силы взаимодействия точек системы между собой: F = Σ [F_i], где F_i = F_i’ + Σ(j ≠ i) F_ji является силой, действующей на материальную точку системы, обозначенную индексом i. Она слагается из внешней силы F_i’ и внутренней силы Σ(i ≠ j) [F_ji], действующей на точку в результате взаимодействия с другими точками системы. Тогда: F = Σ (i=1,n) [F_i’] + Σ (i=1,n) Σ(j ≠ i) [F_ji]. Согласно третьему закону Ньютона Σ (i=1,n) Σ(j ≠ i) [F_ji] = 0, поэтому F = Σ [F_i’]. Моментом силы, действующей на систему материальных точек, называется сумма моментов сил, приложенных к точкам системы M = Σ (i) [M_i] = Σ (i) [r_i * F_i] = Σ (i) [r_i * F_i’]. Для системы материальных точек уравнение движения имеет вид dp / dt = Σ [dp_i / dt] = Σ [F_i].

Центр масс системы материальных точек – это воображаемая точка с радиусом-вектором R = 1/m Σ [m_0i r_i]. Скорость его движения V = dR/dt. Тогда уравнение движения m dV/dt = F. Уравнение моментов для системы материальных точек dL/dt = M. Законы сохранения. Изолированная система – та, на которую не действуют внешние силы. В ней F = 0, поэтому dp/dt = 0. Тогда p = const. В изолированной системе момент внешних сил M = 0. Поэтому dL/dt = 0, а значит L = const. Изменение кинетической энергии материальной точки при ее перемещении между двумя положениями равно работе, совершенной при этом силой. m₀v₂² /2 – m₀v₁² /2 = ∫(1,2) F dl или m₀v² /2 + Е_п = const.

4. Движение в центрально-симметричном поле. Законы Кеплера. Поле называют центральным, если в нем потенциальная энергия тела зависит только от расстояния r до определенной неподвижной точки. Сила F = - ∂U(r)/ ∂r = - dU/dr r/r действующая на частицу, по абсолютной величине зависит при этом тоже только от r и направлена в каждой точке вдоль ра­диус-вектора. При движении в центральном поле сохраняется момент системы относительно центра поля. Для одной частицы момент М = [r*р]. Поскольку векторы М и r взаимно перпендикулярны, по­стоянство М означает, что при движении частицы ее радиус-вектор все время остается в одной плоскости - плоскости, перпендикулярной к М. Таким образом, траектория движения частицы в центральном поле лежит целиком в одной плоскости. Введя в ней полярные координаты r, φ, напишем функцию Лагранжа в виде L = m/2 (r²(∙) + r²φ²(∙)) - U(r). Эта функция не содержит в явном виде координату φ. Для такой координаты соответствующий ей обобщенный импульс p_i является интегралом движения. В данном случае обобщенный импульс р_φ = mr²φ(∙) совпадает с моментом М_z = М, так что M = mr²φ(∙) (1). Заметим, что для плоского движения одной частицы в цент­ральном поле этот закон допускает простую геометрическую интерпретацию. Выражение 1/2 r r d φ представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории. Обозначив ее как df, напишем момент частицы в виде M = 2mf, где производную f называют секториальной скоростью. Поэтому сохранение момента означает постоянство секториальной ско­рости - за равные промежутки времени радиус-вектор движущейся точки описывает равные площади (вто­рой закон Кеплера). Выражая φ(∙) через М из (1) и подставляя в выраже­ние для энергии, получим: E = m/2 (r²(∙) + r²φ²(∙)) + U(r) = mr²(∙)/2 + M²/2mr² + U(r). Отсюда r(∙) = √(2/m (E – U(r)) - M²/m²r²) или, разделяя переменные и интегрируя: t = ∫dr/√(2/m (E – U(r)) - M²/m²r²) + const. Далее, написав (1) в виде dφ = M²/mr² dt, подставив сюда dt и интегрируя, находим: φ = ∫dr (M/r²)/√(2/m (E – U(r)) - M²/r²) + const. Первый закон Кеплера. Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце. Третий закон Кеплера. Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит T₁²/T₂² = a₁³/a₂³.

5. Функция Лагранжа и уравнения Лагранжа системы материальных точек. Интегралы движения. Рассмотрим замкнутую систему материальных точек. Функция Лагранжа для нее имеет вид L = Σ(a) [m_av_a² / 2] – U(r₁, r₂, …), где T = Σ (a) [m_av_a² / 2] – кинетическая энергия, а U – потенциальная энергия взаимодействия частиц. Тогда уравнения движения d/dt (∂L/∂v_a) = ∂L/∂r_a принимают вид m_a dv_a/dt = - ∂U/∂r_a. Эти уравнения движения называются уравнениями Ньютона. Вектор F_a = - ∂U/∂r_a называется силой. Если для описания движения используются не декартовы координаты точек, а произвольные обобщенные координаты q_i, то для получения лагранжевой функции надо произвести соответствующее преобразование: x_a = f(q₁, q₂, .., q_s), x_a(∙) = Σ(k) [∂f_a/∂q_k(∙)] и т. д. Подставляя эти выражения в функцию L= 1 / 2 Σ(a) [m_a (x_a²(∙) + y_a²(∙) + z_a²(∙))] – U, получим искомую функцию Лагранжа вида L = 1/2 Σ(i,k) [a_i,k(q) q_i(∙) q_k(∙)] – U(q). Интегралы движения. Существуют такие функции обобщенных координат, которые сохраняют при движении постоянные значения, зависящие только от начальных условий. Они называются интегралами движения. В силу однородности времени dL/ dt = Σ(i) [∂L/∂q_i q_i(∙)] + Σ(i) [∂L/∂q_i(∙) q_i(∙∙)]. Заменяя ∂L/∂q_i согласно уравнениям Лагранжа на d/dt (∂L/∂q_i(∙)), получим dL/dt = Σ(i) [d/dt (∂L/∂q_i(∙) q_i(∙))] или d/dt (Σ(i) [q_i(∙) ∂L/∂q_i(∙)] - L) = 0. Отсюда видно, что величина Е = Σ(i) [q_i(∙) ∂L/∂q_i(∙)] – L, называемая энергией, не меняется, т.е. интеграл движения. В связи с однородностью пространства при бесконечно малом переносе ε, когда все точки системы смещаются на ε = δr, изменение функции Лагранжа, равное δL = ε Σ(a) [∂L/∂r_a], должно быть равно нулю, т.е. Σ(a) [∂L/∂r_a] = 0. Используя уравнения Лагранжа, получаем Σ(a) [d/dt (∂L/∂v_a)] = d/dt (Σ(a)[ ∂L/∂v_a]) = 0. Тогда величина Р = Σ(a)[ ∂L/∂v_a], называемая импульсом, остается неизменной, т.е. интеграл движения. В связи с изотропностью пространства при бесконечно малом повороте на угол δφ изменение функции Лагранжа, равное δL = Σ(a) [∂L/∂r_a δr_а + ∂L/∂v_a δv_а] должно быть равно нулю. Произведя замену ∂L/∂v_a = p_a и ∂L/∂r_a = p_a(∙) ввиду произвольности δφ получим d/dt Σ(a) [r_ap_a] = 0. Величина М = Σ(a) [r_ap_a], называемая моментом импульса остается постоянной, т.е. интеграл движения.

6. Динамика абсолютно твердого тела. Тензор инерции. Уравнения Эйлера. Твердое тело – система материальных точек, расстояние между которыми остается постоянным. Для полного описания движения твердого тела необходимо кроме движения одной из его точек знать движение тела около этой точки как точки закрепления. Пусть тело закреплено в точке О. Радиус-вектор точки m_i относительно О обозначим r_i, w – мгновенная угловая скорость тела, тогда момент импульса L = Σ [r_i * m_iv_i] = Σ[m_ir_i * (w * r_i)] = w Σ [m_ir_i²] – Σ [m_ir_i(w r_i)]. Это векторное равенство можно записать в виде трех проекций на оси координат L_x = w_x Σ [m_ir_i²] - Σ [m_ix_i(w r_i)]; L_y = w_y Σ [m_ir_i²] - Σ [m_iy_i(w r_i)]; L_z = w_z Σ [m_ir_i²] - Σ [m_iz_i(w r_i)]. Учитывая, что (w r_i) = x_iw_x + y_iw_y + z_iw_z получим L_x = J_xxw_x + J_xyw_y + J_xzw_z; L_y = J_yxw_x + J_yyw_y + J_yzw_z; L_x = J_zxw_x + J_zyw_y + J_zzw_z, где J_xx = Σ [m_i(r_i² – x_i²)], J_xy = Σ [m_ix_iy_i], другие аналогично. Величины J_xx, J_yy, J_zz называются осевыми моментами инерции, а J_xy = J_yx, J_xz = J_zx, J_yz = J_zy – центробежными моментами инерции. Совокупность величин J_ij называется тензором инерции. Элементы J_ii называются диагональными. Если все недиагональные элементы равны нулю, то говорят, что оси тела, совпадающие с осями координат, являются главными осями инерции, а величины J_ii называют главными моментами инерции. Такой тензор приведен к диагональному виду.

Уравнения Эйлера. Уравнение движения центра масс тела имеет вид m dv₀/dt = m d/dt (w * r₀) = F, где r₀ – радиус-вектор центра масс тела, проведенный из точки его закрепления. Оси связанной с телом системы координат удобно направить по главным осям инерции. В этом случае момент импульса приобретает простой вид L₁ = J₁ w₁, L₂ = J₂ w₂, L₃ = J₃ w₃, причем w_i – проекции угловой скорости на движущиеся вместе с телом оси координат. Воспользовавшись общей формулой dA/dt = ∂A/∂t + w * A, можно представить уравнение моментов следующим образом ∂L/∂t + w * L = M. Принимая во внимание, что L_x = J_xw_x, L_y = J_yw_y, L_z = J_zw_z, это уравнение перепишем в проекциях на оси движущейся системы координат: J_x dw_x/dt + (J_z - J_y)w_yw_z = M_x, J_y dw_y/dt + (J_x – J_z)w_zw_x = M_y, J_z dw_z/dt + (J_y – J_x)w_xw_y = M_z. Эти уравнения называются уравнениями Эйлера.

7. Движение относительно неинерциальных систем отсчета. НИСО-это система, в кот. тело движется с ускорением отн-но покоящ. системы коорд. Здесь понятия однородности и изотропности пространства и времени не выполняются, т.к. длительность и протяженность в НИСО меняются. Кроме того, теряется содержание 3 го з-на Ньютона и з-ов сохранения. Причиной всему служат силы инерции, связанные только с системой координат, кот. действуют на движение тела. Т.О. ускорение можно изменять при помощи внешней силы, либо силой инерции. F=∑Fi=ma (ИСО), F=F(внеш.)+Fi=ma′(НИСО), где Fi-сила инерции, a-ускор. тела в ИСО, a′-ускор. того же тела в НИСО. В НИСО 1-й з-н Ньютона не выполняется! Fi=-m(a′-a), т.е. силы инерции не подчиняются 3му з-ну Ньютона, т.к. они кратковремены. При переходе от ИСО к НИСО силы инерции исчезают. Инерц. силы всегда направлены против век. внешних сил. Силы инерции сожно складывать векторно. В ИСО: v=const, v<<c, x, y, z-переменны, a, t, ∆r- постоянны. В НИСО (при малых скоростях): v≠const, y=y′, z=z′, x=x′+v(t)∙t′.

dx/dt=Ux=dx′/dt+dv(t)/dt′=U′x+v(t) dUx/dt=d/dt′(U′x+v(t))=dU′x/dt′+dv(t)/dt′=a_x’ + a₀ = a_x. В НИСО вводятся понятия абсолютной, относительной и переносной скоростей: u₀-абсолютная скорость, a₀- ускорение относит. покоящ. системы коорд.

u_x0 = v + u_x0’; a_x0 = a’ + a_x; u_x’ a_x - скорость и ускорение относит. движ. системы коорд. (относительные) ; v, a′-скор. и ускорен. к′ относит. к, т.е. переносные скорость и ускорение

8. Вариационный принцип Гамильтона. (принцип наименьшего действия).

Существует -функция обобщенной координаты, скорости, времени. Рассмотрим пространство 2S мерное, тогда положение системы S = ∫(t₁, t₂) L(g, g(•), t)dt, L- функция Лагранжа; S- действие. Ф-ей действия наз-ся итнеграл S=∫ Ldt=0, при кот. взятая вдоль истинной траектории движения система будет иметь минимальное значение, т.е. S=Smin, δS=0. Т.е. система из 1 в 2 движется по такой траектории, чтобы её действие было минимально- принцип наименьшего действия Гамильтона. L = T – U -разность кинетической и потенциальной энергий системы. Согласно Гамильтону действительная траектория отвечает минимальному действию. Найдем траекторию. Действительная траектория- минимальная траектория. S-функционал. Найдем её min. δS = 0 первая вариация. δS = ∫(t₁,t₂)(Σ[∂L/∂g_i δg_i] + Σ[∂L/∂g_i(•) δg_i(•)])dt; ∫(t₁,t₂) ∂L/∂g_i(•) δg_i(•) dt = ∫(t₁,t₂) ∂L/∂g_i(•) dδg_i = ∂L/∂g_i(•)δg_i (t₁,t₂) - ∫(t₁,t₂) δg_i d/dt (∂L/∂g_i(•)) dt;

;

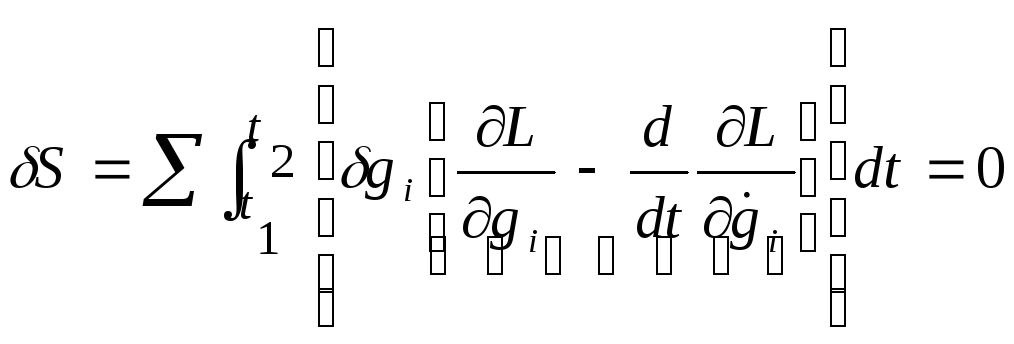
δg_i не зависят друг от друга =0на действительной траектории должно выполняться уравнение:- уравнение Лагранжа (для любыхi= 1,…S ).

9. Колебания систем с одной и многими степенями свободы. Свободные и вынужденные колебания. Наиболее простой случай, когда система имеет одну степень свободы. Устойчивому равновесию соответствует такое положение сис., в кот. ее потенц. эн. U(q) имеет минимум. Отклонение от такого положения приводит к возникновению силы - dU/dq, стремящейся вернуть систему обратно. q₀ - обобщенная координата. Разложим U(q) - U(q0) по степеням и получим U(q) - U(q0) ≈ k/2 (q - q₀)² где к =U’’(q₀) - положительный коэффициент. U(q₀) = 0, обозначим х = q - q₀ - отклонение координаты от равновесного значения, тогда U(x) = kx²/2 – потенц.энергия. 1/2a(q) q’²=1/2a(q)x’²-кинет.энергия при q = q0 и a(q0) = m получим функцию Лагранжа для системы совершающей одномерные колебания: L = mx²(∙)/2 – kx²/2. Соответствующее этой функции уравнение движения будет: mx(∙∙) + kx = 0 или x(∙∙) + w²x = 0, где w = √(k/m) -циклическая частота колебаний. Решением этих ур-й яв-ся х = a cos(wt + α) где а-амплитуда колебаний, wt + α - фаза колебаний. т.о. энергия системы совершающей колебания будет E = mx²(∙)/2 + kx²/2. Вынужденные колебания. В этом случае наряду с собственной потенциальной энергией ½ кх² система обладает еще потенциальной энергией U_e(х,т) связанной с действием внешнего поля. Соответственно функция Лагранжа такой системы будет: L = mx²(∙)/2 + kx²/2 + x F(t), где F(t)-внешняя сила.

Соответствующее ур-ние движения будет mx(∙∙) + kx = F(t), или x(∙∙) + w²x = F(t)/m. Если F(t) яв-ся простой периодической функцией времени с некоторой частотой γ: F(t) = f cos(γt + β) то решением уравнений движения будет: X = a cos(wt + α) + f cos(γt + β)/(m(w² – γ²)) a и α определяются из начальных условий. Т.о. под действием вынуждающей силы система совершает движение представляющее совокупность двух колебаний - с собственной частотой системы w и с частотой вынуждающей силы - γ. Колебания систем со многими степенями свободы. Потенц. эн. системы U(q_i) имеет минимум при q_i=q_i0. Вводя малые смещения x_i = q_i - q_i0 и разлагая по ним U с точностью до членов 2-го порядка получим потенц. энергию: U = 1/2 Σ(i,k) [k_i,k x_i x_k], к_ik=k_ki. Кинет. эн. для такой системы будет 1/2 Σ(i,k) [m_i,k x_i(∙) x_k(∙)], где m_ik=m_ki. Уравнение Лагранжа для такой системы будет: L = 1/2 Σ(i,k) [m_i,k x_i(∙) x_k(∙) - k_i,k x_i x_k]. Тогда dL = Σ(i,k) [m_i,k x_k(∙) dx_i(∙) - k_i,k x_k dx_i]. Ищем x_k(t) в виде x_k = A_kexp(-iwt), А_к- постоянная. Подставляя это в уравнение Лагранжа, получим систему линейных однородных уравнений. Σ(k) [(-w²m_ik+k_ik)A_k] = 0 - характеристическое уравнение, оно имеет s различных корней w²α (α=1,2,….,s) w_α- собственные частоты системы. Частное решение системы имеет вид: x_k = ∆_kα C_α exp(-iw_αt). Общее решение является суммой всех частных решений: x_k = Σ(α) [∆_kα Q_α], где Q = Re (C_α exp(-iw_αt)).

10. Каноническое уравнение Гамильтона. Ряд преимуществ при исследовании вопросов механики представляет описание с помощью обобщенных координат и импульсов переход от одного набора независимых переменных к другому можно совершить путем преобразования Лежандра. В данном случае оно сводится к следующему. Полный дифференциал функций Лагранжа как функция координат и скоростей равен: dL = Σ(i) [∂L/∂q_i] + Σ(i) [[∂L/∂q_i(∙)]. Это выражение можно написать в виде dL = Σ(i) [p_i(∙)dq_i] + Σ(i) [p_idq_i(∙)]. Перепишем его в виде: d(Σ(i) [p_iqi(∙)] – L) = - Σ(i) [p_i(∙)dq_i] + Σ(i) [q_i(∙)dp_i]. Величина, стоящая под знаком дифференциала, представляет собой энергию системы выраженную через координаты и импульсы и она наз-ся гамильтоновой функцией: H(p,q,t) = Σ(i) [p_iqi(∙)] – L. Из диф. равенства dH = - Σ(i) [p_i(∙)dq_i] + Σ(i) [q_i(∙)dp_i] следуют уравнения: q_i(∙) = ∂H/∂p_i, p_i(∙) = - ∂H/∂q_i – это уравнения Гамильтона. В виду их простоты и симметрии они еще наз. каноническими. Скобки Пуассона. Производная по времени от любой функции F обобщенных координат, импульсов и времени будет dF/dt = ∂F/∂t + Σ(i) [∂F/∂q_i dq_i/dt] + Σ(i) [∂F/∂p_i dp_i/dt]. Пользуясь уравнениями Гамильтона мы можем переписать это уравнение в следующем виде: dF/dt = ∂F/∂t + [H, F], где [H, F] = Σ(i) [∂F/∂q_i ∂H/∂p_i - ∂H/∂q_i ∂F/∂p_i] - наз. скобкой Пуассона. Очевидно, что уравнение Гамильтона могут быть записаны с помощью скобок Пуассона.

11. Уравнение Гамильтона–Якоби. По принципу наименьшего действия имеем S = ∫(t₁,t₂)Ldt. Рассмотрим действие (S) как величину, характеризующую движение по истинным траекториям. Исходя из ур-й Лагранжа для изменения действия при переходе от одной траектории к близкой к ней другой траектории (при одной степени свободы) получим: δS = pδq или для любого числа степеней свободы: δS = Σ(i) [p_iδq_i]. Отсюда следует, что частные производные от действия по координатам равны соответствующим импульсам: ∂S/∂q_i = p_i(1). По определению dS/dt = L с другой стороны рассматривая S как функцию координат и времени и используя формулу (1) имеем: dS/dt = ∂S/∂t + Σ(i) [∂S/∂q_i q_i(∙)] = ∂S/∂t + Σ(i) [p_iq_i(∙)]. Сравнивая оба выражения, получим ∂S/∂t = L - Σ(i) [p_iq_i(∙)] или ∂S/∂t = - H(p,q,t) (2). Формулы (1), (2) можно вместе записать в виде dS = Σ(i) [p_idq_i] – Hdt. А само действие (S) будет S = ∫ (Σ(i) [p_idq_i] – Hdt). При H независимом от t – S(q,t)=S₀(q) - Et, где S₀(q) = Σ(i) [∫p_idq_i] - укороченное действие и Еt заменено H(p,q). Функция S(q,t) удовлетворяет определенному диф. уравнению, которое мы получим, заменив в соотношении (2) импульсы Р производными ∂S/∂q : ∂S/∂t + H(∂S/∂q₁,…, ∂S/∂q_s;q₁,…,q_s,t) = 0 - это уравнение в частных производных 1-го порядка наз. уравнением Гамильтона-Якоби. Так, для одной частицы во внешнем поле U(x,y,z,t) оно имеет вид: ∂S/∂t + 1/(2m)((∂S/∂x)² + (∂S/∂y)² + (∂S/∂z)²) + U(x,y,z,t) = 0.

12. Деформации и напряжения в твердых телах. Модули Юнга, сдвига. Коэффициент Пуассона. Деформация – изменение формы и объема тела под действием внешних сил. Под действием внешней силы форма тела меняется. Все деформации в природе могут быть сведены к 3 м основным деформациям: 1) растяжение, сжатие; 2) сдвига; 3) кручение. Различают однородные и неоднородные деформации. Если все части деформируются одинаково, то это однороднодеформированные. Если все части тела деформируются неодинаково, то это неоднороднодеформированные. Закон Гука выполняется в области только упругой деформации.  = E’. F/S = E ∆l/l₀; F_упр = ES∆l/l₀ = kx; k = ES/l₀; F_упр = ESx/l₀. Закон Гука определяет связь между  и . к-коэффициент упругости, он зависит от геометрических размеров, материала, из чего сделано тело. Е- модуль Юнга. Модуль Юнга равен силе, которую необходимо приложить к телу единичного поперечного сечения, чтобы его тела увеличилась в 2 раза. Другим видом деформирования является деформация сдвига, она наблюдается при касательном приложении поверхности; она параллельна поверхности деформации сдвига, наблюдается при действии тангенциальных сил, т.е., силы приложены касательно. Ψ~F_t/S (угол сдвига). Ψ = nF_t/S; n- коэффициент сдвига. F_t= nS. (Е> N, E~ 4N).

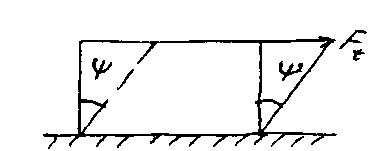Количественная связь между Е и N задается через коэффициент Пуассона. N = E/(2(1+μ)), где  - коэффициент Пуассона. μ = |∆d/d₀|/|∆l/l₀|. Коэффициент Пуассона определяет изменением поперечных размеров при растяжении или сжатии.  0,5.

13. Механика жидкостей и газов. Для всех жидкостей и газов объединяющим параметром является: плотность ρ, давление P=F_n/S. В жидкостих и газах имеет место модуль Юнга, но не имеет место модуль сдвига |σ|=|P|, σ - напряжение. Если жидкость (газ) неподвижны то имеем дело с гидростатикой (аэростатикой). Характерные законы: З-н Паскаля: избыточное давление, создаваемое в газах и жидкостях передается во все стороны одинаково. З-н Архимеда справедлив и для жидкостей и для газов. Сила Архимеда всегда действует против силы тяжести. Причиной возникновения силы Архимеда является наличие у тела объема V. З-н Архимеда: На тело находящееся в жидкости или газе всегда действует сила равная весу жидкости или газа, вытесненного погруженной частью тела, и направленная вертикально вверх. Если F_A>F_ТЯЖ, то тело всплывает, если наоборот, то – тонет. Если жидкость (газ) текут, то к этим уравнениям присоединяются уравнение непрерывности струи. Траекторию движения частицы в жидкости наз. линией тока. Часть пространства ограниченная линией тока наз. трубкой тока. Жидкость в трубке тока может течь стационарно или не стационарно. Течение наз. стац. если через данное сечение трубки тока за ед. времени проходит одинаковое кол-во жидкости (газа), иначе, течение нестац. Пусть мы имеем трубку тока следующего вида: Если течение жидкости стац. То m₁=m₂=…=m_n за единицу времени, если жидкость несжимаема, то ρ₁V₁=ρ₂V₂=…; =ρ_nV_n, ρ₁Δx₁= ρ₂Δx₂=…; = ρ_nΔx_n, ρ₁υ₁ΔtS₁=ρ₂υ₂ΔtS₂=…= ρ_nυ_nΔtS_n, т. К. жидкость несжимаема ρ постоянно υ₁S₁=υ₂S₂=…= υ_nS_n, υS=const; υ=const/S – уравнение неразрывности струи. ρ dv/dt = ρg – grad P – уравн. Эйлера – 2-й зак. Ньютона для жидкостей и газов. Закон сохр. Энергии в жидкостях и газах. Ур. Бернулли. Ид. Наз. Несжимаемая жидкость, в которой можно пренебречь силами вязкого трения. Кинетическая энергия не тратится на совершение работы против сил трения. Ρυ­­²/2+ρgh + P = const – ур. Бернулли, ρυ­­²/2 – динамическое давление, ρgh – гидростат. Давл., P – молекулярное давление. Mυ­­²/2 = E_K; mυ­­²/2V= E_K/V= ρυ­­²/2. Сила вязкого трения F_A= - ηΔυΔS/ΔZ  6 π r η υ – сила Стокса. Η - коэф. вязкости, Δυ/ΔZ – grad υ, r – размеры тела. Это есть формула Ньютона для сил вязкого трения. Если в жидкости имеются силы трения, то ид. Жидкость стан-ся вязкой. ρ v₁²/2 + ρgh₁ + P₁ = ρ v₂²/2 + ρgh₂ + P₂; (P₁ – P₂)= ρ(υ­₂­² – υ­₁­²)/2. Если ΔP = 0, то υ­₂­² – υ­₁­² = 0, и течения жидкости не будет. Где P больше, там скор. Течения меньше. Если сечение S растет, то растет P и падает υ. Если трубка тока не лежит горизонтально, то υ­₂­²-υ­₁­² =2g (h₁-h₂); υ = sqrt(2g (h₁-h₂)) – формула Торричелли.