Закони розподілу дискретних випадкових величин

Біноміальний розподіл (розподіл Бернуллі)

Цей розподіл застосовують в ситуаціях, коли цікавляться частотою деякої події в серії незалежних випробувань. Подія може відбутися або ні

Дискретна випадкова величина Xназивається розподіленою за біноміальним законом, якщо вона може приймати тільки цілі невід’ємні значення з ймовірностями

де р– ймовірність появи події в кожному випробуванні,

q=1–p- ймовірність того, що подія не відбулася,

m– кількість сприятливих подій,

п– загальна кількість випробувань,

-біноміальний коефіцієнт. (Це ймовірність того, щоnнезалежних випробуваннях, у кожному з яких ймовірність появи події дорівнюєp, ця подія наступить рівноmразів).

Математичне сподіванняпри біноміальному розподілі дорівнюєMX=nр,

а дисперсія–=npq.

Наприклад: У лабораторії проводять експерименти з дослідження вірусів. 2-м щурам ввели вірус В₁, 3-м – вірус В₂і 5-ти – вірус В₃. Ймовірність зараження вірусом В₁дорівнює 0.1, вірусом В₂– 0.3 і вірусом В₃– 0.5. Навмання взятий щур виявився зараженим. Який вірус найімовірніше йому вводили?

Усього маємо n=10 щурів. Навмання взятий щур виявиться зараженим вірусом В₁з ймовірністю:

вірусом В₂

вірусом В₃

Отже, найймовірніше, що навмання взятий щур виявиться зараженим вірусом В₂.

Розподіл Пуассона

Дискретна випадкова величина Х, називається розподіленою за законом Пуассона з математичним сподіванням і дисперсією, якщо вона приймає цілі невід’ємні значення з ймовірностями

.

λ– параметр розподілу Пуассона.

Тут розглядаються ймовірність того, що рідкісна подія, яка нас цікавить, відбудеться mразів під час довгої серіїnнезалежних випробувань.

Оцінити значення можна за формулою

=np,

де n– кількість фактично проведених спостережень,

p– ймовірність появи рідкісної події в одному спостереженні.

Розподіл Пуассона може розглядатися як граничний випадок біноміального розподілу. Розподіл Пуассона інколи називають розподілом рідкісних подій.

Наприклад: Вакцина формує імунітет від деякого захворювання з ймовірністю 0,999. Провакциновано 4000 мешканців міста. Яка ймовірність того, що двоє з них не набули імунітету.

• ймовірність того, що імунітет не сформовано – р=1-0,999=0,001

• 

• .

Закони розподілу неперервних випадкових величин Нормальний закон розподілу (Гаусса)

У біології та медицині найчастіше розглядають випадкові величині, які мають нормальний закон розподілу, наприклад, частота дихання, частота серцевих скорочень, динаміка росту популяції тощо.

Нормальний розподіл використовуються для опису реальних явищ, у яких:

• присутня сильна тенденція даних групуватися навколо центру,

• додатні та від'ємні відхилення від центру рівноймовірні,

• частота відхилень швидко спадає, коли відхилення від центру стають великими.

Для нормального закону розподілу щільність розподілу задається рівнянням:

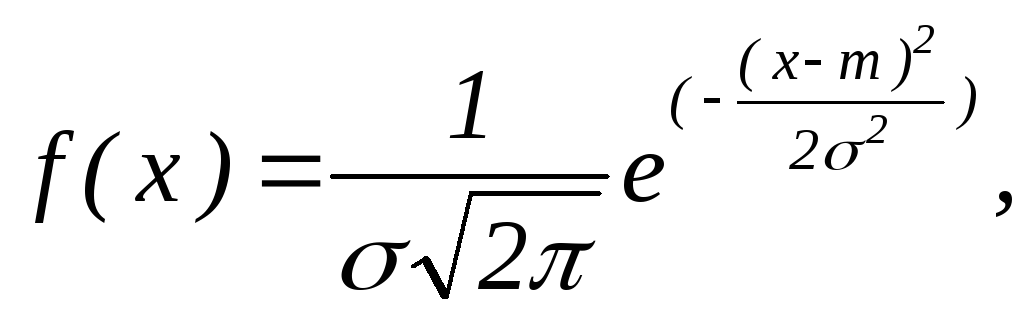
де m– математичне сподівання, а– середнє квадратичне відхилення.

Середнє квадратичне відхилення характеризує розсіювання випадкової величини.

Стандартним нормальним розподілом N(0,1)називають розподіл з нульовим математичним сподіваннямm=0і одиничною дисперсією=1, щільність розподілу якого має наступний вигляд:

Графік функції щільності нормального розподілу називають нормальною кривою або кривою Гаусса (рис. 2). Якщоm=0 іσ=1, то ця функція називається функцією Лапласа.

Рис. 2

Функція щільності нормально розподіленої випадкової величини

Правило трьох сигм.Якщо закон розподілу випадкової величиниX невідомий, але

тоді можна припустити, що випадкова величина X розподілена нормально.