6.6. Проверка гипотезы однородности двух выборок (критерий Вилксона)

Критерий Вилксона служит для проверки гипотезы принадлежности двух выборок единой генеральной совокупности. Он нашел большое распространение по двум причинам. Во-первых, в силу своей простоты, во-вторых, этот критерий не предъявляет каких-либо требований к функции плотности распределения генеральной совокупности. Это критерий относится к группе, так называемых, непараметрических критериев.

Критерий Вилксона основан на вычислении рангов двух выборок. Рассмотрим методику расчета рангов на конкретном примере. В начале создадим таблицу данных. Подготовим таблицу сразу для решения двух примеров.

Первый шаг. Сгенерируем четыре нормальных выборки с параметрами:

- объемом;

- объемом;

- объемом;

- объемом.

Второй шаг. Преобразуем данные столбцов путем округления с точностью до трех знаков. Результаты разместим в столбцах. Для этого будем использовать программу ОКРУГЛ. Интерфейс программы представлен на рис. 6.40. Полученная таблица данных приведена на рис. 6.41. Операция округления произведена для тог чтобы смоделировать ситуацию приближенную к реальной. При округлении в столбцахбудут встречаться одинаковые значения, что соответствует реальным ситуациям.

Теперь возвратимся к исходной постановке задачи применительно к созданной таблице данных. Проверим гипотезу о том, что данные двух выборок иможно считать принадлежащими одной генеральной совокупности.

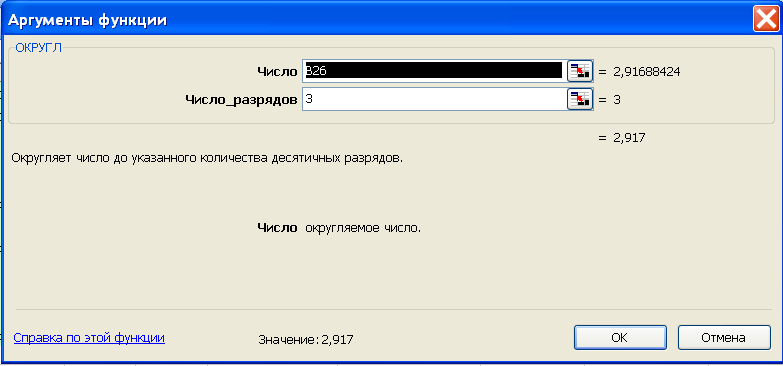
Рис. 6.40. Выполнение операции округления

Рис. 6.41. Таблица данных

Объединим данные обоих выборок в единую выборку. Объединенную выборку разместим в столбце . В столбцевначале расположим значения выборки из столбца, а затем из столбца. Всего столбецбудет содержать 100+120=220 значений. Введем в таблицу данных три дополнительных столбца: ”№ выб. по Z1”, “Контроль по Z1”, “Ранг по Z1” (рис. 6.42). Первы два столбца носят вспомогательный характер. В столбце ”№ выб. по Z1” содержатся номера выборок. Назначение столбца “Контроль по Z1” поясним ниже. Для выполнения дальнейших действий необходимо установить на всю таблицу автофильтр. Автофильтр устанавливается в меню“Данные” (Фильтр-автофильтр).

Рис. 6.42. Таблица для расчета рангов (сортировка по столбцу ”№”)

Теперь приступим к определению рангов для элементов объединенной выборки. Для этого вначале с помощью автофильтра отсортируем таблицу данных по возрастанию значений в столбце . Ранг значения определим, как порядковый номер значения в упорядоченной последовательности значений. Если бы все значения в последовательностибыли различны, то ранги значений в нашем примере принимали бы значения натуральных чисел от 1 до 220. Но на практике в выборке могут в упорядоченной последовательности могут встретиться одинаковые числа. Для одинаковых значений ранг определяется как среднее значение их порядковых номеров. Для того чтобы не упустить повторяющиеся значения и служит вспомогательный столбец “Контроль по Z1”. О повторяемости значений будет сигнализировать какое-нибудь установленное значении (в нашем случае 1). Определение рангов по столбцупоказано на рис. 6.43. Сумма рангов по столбцу и с неповторяющимися значениями и с повторяющимися будет равна сумме ряда натуральных чисел. Для последовательности изmзначений сумму чисел можно определить по формуле:

(6.26)

Для нашего примера:

(6.27)

Рис. 6.43. Расчет ранга по столбцу

После расчета рангов вернем таблицу в исходное состояние путем сортировки по возрастанию значений в столбце ”№”. Рассчитаем сумму рангов по каждой из выборок и:

(6.28)

Сумма рангов по двум выборкам будет равна сумме рангов объединенной выборки:

(6.29)

Если принять гипотезу, что обе выборки принадлежат одной генеральной совокупности, то логично предположить, что в сортированной выборке значения обоих выборок разместятся случайным образом. Тогда математическое ожидание суммы рангов должно зависеть только от числа элементов выборки и соответственно определяться по формулам:

(6.30)

(6.31)

В теории доказывается, что при случайном распределении номеров выборок в упорядоченной объединенной выборке дисперсия суммы рангов определяется по формуле:

(6.32)

Случайные величины иподчиняются нормальному закону. Пронормируем выборочные значения. Получим выборочные значения критерия Вилксона:

(6.33)

(6.33)

Значение критерия для двух выборок исовпадают с точностью до знака. Поэтому можно использовать одно значение критерия. С учетом нормировки для проверки выдвинутой гипотезы, можно использовать стандартное нормальное распределение. Поскольку критерий может принимать и положительные значения и отрицательные необходимо использовать двухстороннюю критическую область. То есть, при уровне значимости 0,05 для односторонней области необходимо выбирать. Критическое значение можно определить по справочнику стандартного нормального распределения либо с помощью функции НОРМОБР (рис. 6.44).

Рис. 6.44. Определение критического значения с помощью функции НОРМОБР

Выборочное значения критерия Вилксона меньше критического =1,96, поэтому выдвинутую статистическую гипотезу можно принять. Расчет параметров, необходимых для проверки гипотезы с помощью критерия Вилксона, представлен на рис. 6.45.

Рис. 6.45. Расчет параметров для проверки гипотезы по критерию Вилксона