ТЕОРИЯ ВЕРОЯТНОСТИ 2014 / Решение задач по теории вероятностей

1.Задача. Сколько элементарных исходов благоприятствует событию «на обоих кубиках выпало одинаковое количество очков» при подбрасывании двух игральных кубиков?

Решение: Этому событию благоприятствуют 6 элементарных исходов (1;1), (2;2), (3;3), (4;4), (5;5), (6;6).

2.Задача. Подбрасываются три игральных кубика, подсчитываются сумма очков, выпавших на них. Сколькими способами можно получить в сумме 5 очков, 6 очков?

Решение: Получить в сумме 5 очков можно шестью способами: (1;1;3), (1;3;1), (1;1;3), (1;2;2), (2;1;2), (2;2;1). Получить в сумме 6 очков можно десятью способами (1;1;4), (1;4;1), (4;1;1), (1;2;3), (1;3;2), (2;1;3), (2;3;1), (3;1;2), (3;2;1), (2;2;2).

3.Задача. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После перемешивания из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5, 4, 3?

Решение: Обозначим через А событие «число на взятой карточке кратно 5». В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию А благоприятствую 6 исходов (числа 5, 10,15,20,25,30). Следовательно

Р(А)= 6/30= 0,2

4. Задача. Произвольно выбрано натуральное число, не превосходящее 10. Какова вероятность того, что это число является простым?

Решение: Обозначим буквой С событие «выбранное число является простым». В данном случае n=10, m=4 (простые числа 2, 3, 5, 7). Следовательно, искомая вероятность

Р(С)=4/10=0,4.

5. Задача. Какова вероятность того, что в произвольно выбранном двузначном числе цифры одинаковы?

Решение: Двузначными числами являются числа от 10 до 99; всего таких чисел 90. Одинаковые цифры имеют 9 чисел (это числа 11, 22, 33, 44, 55, 66, 77, 88, 99). Так как в данном случае m=9, а n=90, то

Р(А)=9/90=0,1

6. Задача. Подбрасываются две монеты. Чему равна вероятность того, что на верхних сторонах монет окажутся две цифры?

Решение: Обозначим буквой D событие «на верхней стороне каждой монеты оказалась цифра». В этом испытании 4 равновозможных элементарных исходов (Г;Г), (Г;Ц), (Ц;Г), (Ц;Ц). Запись (Г;Ц) означает, что на первой монете выпал герб, а на второй – цифра. Событию D благоприятствует один исход - (Ц;Ц).Поскольку m=1, а n=4, то

Р(D)=1/4=0,25.

7. Задача. В книге 300 страниц. Чему равна вероятность того, что произвольным образом открытая страница будет иметь порядковый номер, кратный 5?

Решение: Из условия задачи следует, что всех равновозмож-ных элементарных исходов, образующих полную группу событий, будет n=300. А из них m=60 благоприятствует наступлению указанного события. Действительно, номер, кратный 5, имеет вид 5k, где k- натуральное число, причем 0<5k<300, откуда k<300/5=60. Следовательно

P(А)= 60/300=0,2

8. Задача. Сколькими различными способами можно разместить на скамейке 5 человек?

Решение: Согласно формуле для перестановок для n=5 имеем

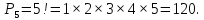
9. Задача. Сколькими способами можно выбрать три лица на три одинаковые должности из 10 кандидатов?

Решение: В соответствии с формулой для числа сочетаний С (а в данном случае речь идет именно о сочетаниях, поскольку нужно определить число возможных комбинаций по 3 элемента в каждой из 10 имеющихся в наличии, не взирая на порядок следования этих элементов внутри комбинации), находим

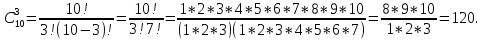
10. Задача. Сколькими способами можно выбрать три лица на три различные должности из 10 кандидатов?

Решение: Для получения результата воспользуемся формулой для числа размещений 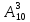по 3 элемента из десяти, поскольку в данном случае необходимо учесть в отличие от задачи девять не только число возможных комбинация, но и порядок следования элементов внутри каждой комбинации.

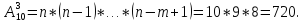
11. Задача. Сколько различных шестизначных числа можно записать с помощью цифр 1;1;1;2;2;2?

Решение: В данном случае речь идет о числе перестановок с повторениями. Тогда формула для вычисления перестано-вок будет иметь вид

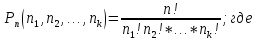
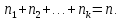
Для нашего случая число символов, которые повторяются k=2,повторяются они каждый по три раза 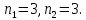А общее число символов n= 3+3=6. По приведенной формуле получаем

12. Задача. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди взятых наугад 6 деталей 4 окажется стандартными?

Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 разных деталей из 10 имеющихся в наличии, т.е. числу сочетаний из 10 элементов по 6 элементов

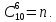
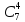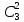Определяем число исходов, благоприятствующих событию A – «среди взятых наугад 6 деталей 4 стандартных». Четыре стандартных из имеющихся в наличии 7 можно взять способами, при этом остальные 6-4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10-7=3 нестандартных деталей можно способами. Следовательно, число благоприятных исходов равно 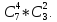Следует обратить особое внимание, что сумма верхних и нижних индексов в последнем произведении дает значение верхних и нижних индексов знаменателя формулы для определения вероятности события

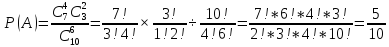
13. Задача. Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Найти вероятность того, что среди обладателей билетов окажутся 2 девушки?

Решение: Число всех равновозможных случаев распределе-ния 5 билетов среди 25 студентов равно числу сочетаний из 25 элементов по 5, т.е. 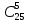. Число групп по трое юношей из 15, еоторые могут получить билеты, равно 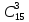. Каждая такая тройка должна сочетаться с любой парой девушек, которые будут отобраны из 10 оставшихся студенток группы, а это число будет равно 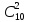. Следовательно, число удовлетворяющих условию задачи групп студентов по пять человек в каждой, где будет 3 юноши и 2 девушки, равно произведению 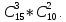Это произведение равно числу благоприятствующих случаев распределения 5 билетов среди 25 учащихся таким образом, чтобы было выполнено условие: 3 билета досталось юношам, а два – девушкам. И тогда в соответствии с формулой определения вероятности получаем

14. Задача. В ящике находится 15 красных, 9 синих и 6 зелёных шаров. Наугад извлекают 6 шаров. Найти вероятность того, что вынуты 1 зелёный, 2 синих и 3 красных шара.

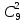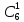Решение: В ящике всего 30 шаров. При данном испытании число всех равновозможных элементарных исходов будет Подсчитаем число элементарных исходов, благоприят-ствующих событию A. Три красных шара из 15 можно выбрать способами, два синих шара из 9 возможных можно выбрать способами, один зеленый из 6 - способами. Следовательно, в силу принципа произведения в комбинаторике, число исходов, благоприятствующих событию A, будет 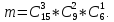По формуле непосредственного подсчета вероятностей получаем

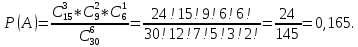
15. Задача. В ящике находятся 15 шаров, из которых 10 красных, остальные синие. Из ящика вынимают 6 шаров. Найти вероятность того, что среди вынутых 2 шара синего цвета?

Решение: Общее число элементарных исходов данного опыта равно числу сочетаний из 15 по 6, т.е.

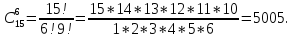
Число благоприятных исходов равно произведению

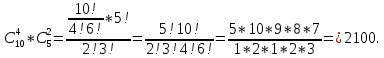
Тогда вероятность искомого варианта составит величину

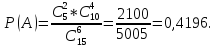
16. Задача. Из десяти билетов выигрышными являются только два. Чему равна вероятность того, что среди взятых наугад пяти билетов один выигрышный?

Решение: Общее число исходов, когда из десяти наличных билетов мы выбираем пять, определяется числом сочетаний 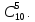А число благоприятных исходов определим как произ-ведение двух сомножителей 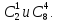Отсюда вероятность определяем как

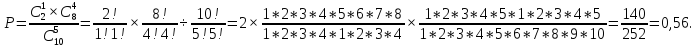
17. Задача. Из 500 взятых наугад деталей оказалось 8 бракованных. Найти частоту бракованных деталей.

Решение: Так как в данном случае m=8, а n=500, то согласно определению частоты события имеем

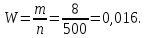
18. Задача. Среди 1000 новорожденных оказалось 513 мальчиков. Чему равна частота рождения мальчиков?

Решение: Поскольку в данном случае m=513, а n=1000, то

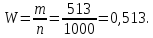
19. Задача. При стрельбе по мишени частота попаданий составляет W=0,75. Найти число попаданий при 40 выстрелах.

Решение: Из условия задачи имеем n=40, а найти необходимо m. Тогда получаем

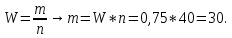
20. Задача. Частота нормальной всхожести семян W=0,75.Из высеянных семян взошло 1940. Сколько семян было высеяно?

Решение: Из условия задачи m =1940, а определить необхо-димо n.

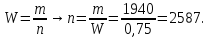
21. Задача. На отрезке натурального ряда от 1 до 30 найти частоту простых чисел?

Решение: На указанном отрезке натурального ряда чисел находятся следующие простые числа 2,3,5,7,11,13,17,19,23, 29; всего их десять. Так как n=30, а m=10, то

22. Задача. В круг вписан квадрат. В круг бросают дротик. Определить вероятность того, что дротик попадёт в квадрат.

Решение: Введем обозначение: R – радиус круга, a - сторона вписанного в круг квадрата, событие A – попадание дротика в квадрат, S – площадь круга, S₁ – площадь вписанного квадрата. Как известно, площадь круга Площадь квадрата определяется как 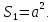Теперь выразим сторону квадрата через радиус круга, используя теорему Пифагора

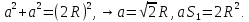
По определению геометрической вероятности имеем

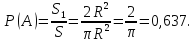
23. Задача. В шар вписан куб. Точка наугад зафиксирована внутри шара. Найти вероятность того, что точка попадёт в куб.

Решение: самостоятельно.

24. Задача. Опыт состоит в том, что стрелок производит 3 выстрела. Событие А_к – «попадание в мишень при к-том выстреле(к=0,1,2,3)». Выразить через А₁, А₂, А₃ следующие события: А- «хотя бы одно попадание», В- «три попадания», С- «три промаха», D- «хотя бы один промах».

Решение: Событие A тогда и только тогда , когда наступает A₁, или A₂, или A₃. Это означает, что A=A₁+A₂+A₃. Три попадания будет тогда и только тогда, когда попадание наступит при каждом выстреле, т.е. события наступят все вместе B=A₁*A₂*A_3. Три промаха будет тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события 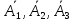осуществляются все вместе: Рассуждая аналогично, получаем выражение для .

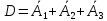25. Задача. Опыт состоит в том, что стрелок производит 3 выстрела. Событие А_к – «попадание в мишень при к-том выстреле(к=0,1,2,3)». Выразить через А₁, А₂, А₃ следующие события: А- «хотя бы одно попадание», Е- «не меньше двух попаданий», F- «не более одного попадания», G- «попадание после первого выстрела».

Решение: Событие A тогда и только тогда , когда наступает A₁, или A₂, или A₃. Это означает, что A=A₁+A₂+A₃. По аналогии с задачей 24 для события Е имеем

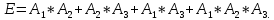
Событие F получим в виде .

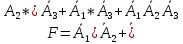Событие G будет получено .

26. Задача. Подбрасывают два игральных кубика. Чему равна вероятность того, что сумма очков, выпавших на обоих кубиках, не превысит 5?

Решение: Пусть выпало на первом кубике, а - на втором кубике. Пространство элементарных событий есть множество пар (n₁, n₂):

Событие А имеет вид

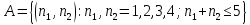
Множество Ω содержит 36 элементов (6*6) , а множество А – 10 элементов (1,1); (1,2); (2,1); (2,2); (2,3); (3,2); (1,3); (3,1); (1,4); (4,1). По известной формуле получим значение вероятности

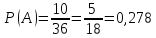
27. Задача. Подбрасываются два игральных кубика. Найдите вероятность того, что сумма очков на обоих кубиках не больше 6.

Решение: Самостоятельно.

28. Задача. В лотерее разыгрывается 100 билетов. Выигрыш выпадает на 13 билетов. Некто купил 4 билета. Какова вероятность того, что хотя бы один из них выиграет?

Решение: Общее число возможных исходов , когда производится выбор 4 билетов из 100 возможных определяется как 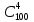. Число благоприятствующих исходов будет определяться как произведение Тогда вероятность приобрести выигрышный билет выразиться следующим выражением

29. Задача. В урне 40 шаров: 15 синих, 5 зеленых и 20 белых. Какова вероятность того, что произвольно вынутый из урны шар окажется цветным?

Решение:

30. Задача. Подбрасываются два игральных кубика. Найти вероятность того, что сумма выпавших очков не превосходит 4?

31. Задача. Спортсмен стреляет по мишени, разделенной на три сектора. Вероятность попадания в первый сектор составляет 0,4, во второй – 0,3. Какова вероятность попадания либо в первый, либо во второй сектор?

32. Задача. Монета подброшена три раза. Какова вероятность того, что цифра выпадет ровно два раза?

33. Задача. Три стрелка стреляют по мишени и попадают с вероятностями 0,85; 0,8; 0,7 соответственно. Найти вероятность того, что при одном выстреле мишень окажется поврежденной.

34. Задача. В урне 6 синих, 5 красных и 4 белых шара. Из урны поочередно извлекают три шара, не возвращая их обратно. Найти вероятность того, что первым будет синий шар, вторым – красный, а третьим – белый.

35. Задача. В каждом из трёх ящиков находится по 30 деталей. В первом ящике 27, во втором – 28, в третьем – 25 стандартных деталей. Из каждого ящика вынимают по одной детали. Какова вероятность того, что все три детали будут кондиционными?

37. Задача. В мастерской независимо друг от друга работает два мотора. Вероятность отказа первого мотора в течении часа составляет 0,85, а второго – 0,8. Найти вероятность того, что в течении часа ни один из моторов не откажет.

38. Задача. Из урны, содержащей 3 синих и 2 красных шара, по схеме случайного выбора без возвращения последовательно извлекаются шары. Найти вероятность P_k того, что красный шар впервые появится при k – том испытании (k=1;2; 3; 4).

39. Задача. Сколько раз надо подбросить два игральных кубика, чтобы вероятность выпадения хотя бы один раз двух шестёрок была бы больше ½? (задача де Мере).

40. Задача. Вероятность того, что событие появится хотя бы один раз в трёх независимых испытаниях, равна 0,973. Найти вероятность появления события в одном испытании, полагая её величиной постоянной.

41. Задача. В урне находится 10 красных и 5 синих шаров. Последовательно извлекают по схеме бесповторного опыта два шара. Определить вероятность того, что в первый раз извлечен синий шар, а во второй раз красный шар.

42. Задача. На фабрике, изготовляющей болты первая машина производит 30%, вторая – 25%, а третья – 45% всех изделий. Брак в их продукции составляет 2%, 1%, 3% соответствен-но. Найти вероятность того, что произвольно выбранный болт оказался бракованным.

43. Задача. В партии электроламп 20% выпущено на первом заводе, 30% - на втором и 50% на третьем. Вероятности выпуска брака заводами составляют 0,01; 0,005 и 0,006 со- ответственно. Найти вероятность того, что произвольно взятая из партии лампочка окажется работоспособной.

44. Задача. На сборку попадают запчасти с трёх автоматов. Из- вестно , что первый автомат даёт 0,1% брака, второй – 0,2%, а третий – 0,3%. Найти вероятность попадания на сборку бракованной детали, если первый автомат выпустил 1000 деталей, второй – 2000, а третий – 3000 запчастей.

45. Задача. Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака от первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обрабатываемые детали складываются в один ящик. Производительность первого станка в три раза выше, чем второго, а третьего в два раза меньше, чем второго. Какова вероятность того, что взятая случайным образом деталь будет стандартной.

46. Задача. Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака от первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обрабатываемые детали складываются в один ящик. Производительность первого станка в три раза выше, чем второго, а третьего в два раза меньше, чем второго. Какова вероятность того, что взятая случайным образом деталь будет бракованной.

47. Задача. Радиолампа может принадлежать к одной из трёх партий с вероятностями: p₁=0,2; p₂=0,3; p₃=0,5. Вероятность того, что лампа проработает заданное количество часов, для этих партий соответственно равна: 0,9; 0,8 и 0,7. Определить вероятность того, что радиолампа проработает заданное время.

48. Задача. В учебной группе студентов учатся 5 отличников, 10 хорошистов и 6 слабоуспевающих . На экзамене отличник может получить только отлично. Хорошист с равной вероятностью получит отличную или хорошую оценку. Слабоуспевающий студент с равной долей успеха может получить хорошую, удовлетворительную и неудовлетворительную оценку. Для сдачи контрольного среза приглашают трёх человек из этой группы. Найти вероятность того, что они получат отличные оценки.

49. Задача. В учебной группе студентов учатся 5 отличников, 7 хорошистов и 8 слабоуспевающих . На экзамене отличник может получить только отлично. Хорошист с равной вероятностью получит отличную или хорошую оценку. Слабоуспевающий студент с равной долей успеха может получить хорошую, удовлетворительную и неудовлетворительную оценку. Для сдачи контрольного среза приглашают трёх человек из этой группы. Найти вероятность того, что они получат хорошие оценки.

51. Задача. В учебной группе студентов учатся 6 отличников, 10 хорошистов и 4 слабоуспевающих . На экзамене отличник может получить только отлично. Хорошист с равной вероятностью получит отличную или хорошую оценку. Слабоуспевающий студент с равной долей успеха может получить хорошую, удовлетворительную и неудовлетворительную оценку. Для сдачи контрольного среза приглашают трёх человек из этой группы. Найти вероятность того, что они получат отличные и хорошие оценки.

52. Задача. На склад поступает продукция трёх фабрик, причём продукция первой фабрики составляет 20%, второй – 46%, и третье-34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, для третьей – 1%. Найти вероятность того, что случайным образом выбранное изделие окажется продукцией первой фабрики.

53. Задача. Некоторое изделие выпускается двумя заводами. При этом объём продукции второго завода в три раза превосходит объём продукции первого. Доля брака у первого завода составляет 2%, у второго – 1%. Изделия поступают на общий склад. Найти вероятность того, что приобретённое в магазине изделие изготовлено на втором заводе, если оно оказалось испорченным.

54. Задача. Некоторое изделие выпускается двумя заводами. При этом объём продукции второго завода в два раза превосходит объём продукции первого. Доля брака у первого завода составляет 0,5%, у второго – 0,2%. Изделия поступают на общий склад. Найти вероятность того, что приобретённое в магазине изделие изготовлено на первом заводе, если оно оказалось исправным.

55. Задача. В первой урне 2 синих и 6 красных шаров, во второй – 4 синих и 2 красных. Из первой урны во вторую переложили 2 шара, не обращая внимания на их цвет, и после этого достали из неё один шар. Определить вероятность того, что этот шар окажется синим.

56. Задача. Подбрасываются два игральных кубика и подсчитывается число очков, выпавших на обоих кубиках. Найти закон распределения случайной величины X - суммы выпавших очков на двух игральных кубиках.

57. Задача. В коробке 7 карандашей, из которых 4 – красные. Из коробки случайным образом достают 3 карандаша. Найти закон распределения случайной величины X, равной числу красных карандашей в выборке.

58. Задача. Закон распределения дискретной случайной величины задан следующей таблицей.

X	0	1	2	3
P	0,2	0,4	0,3	0,1

Найти функцию распределения этой случайной величины.

55. Задача. В первой урне 2 синих и 6 красных шаров, во второй – 4 синих и 2 красных. Из первой урны во вторую переложили 2 шара, не обращая внимания на их цвет, и после этого достали из неё один шар. Определить вероятность того, что этот шар окажется синим.

Решение: Введём обозначение «А» - событие «шар, извлечённый из второй урны – синий»; гипотезы Н₁ – «из первой урны во вторую переложены два синих шара» , Н₂ – «переложены два разноцветных шара» , Н₃ – «переложены два красных шара». Вычислим вероятности гипотез Н_i и условные вероятности Р(А/Н_i), (i=1,2,3):

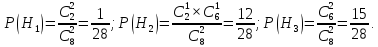
P(A/H₁)=3/4; P(A/H₂)=5/8; P(A/H₃)=1/2.

По формуле полной вероятности получаем ответ на вопрос

Р(А)=1/28*3/4+12/28*5/8+15/28*1/2=9/16

56. Задача. Подбрасываются два игральных кубика и подсчитывается число очков, выпавших на обоих кубиках. Найти закон распределения случайной величины X - суммы выпавших очков на двух игральных кубиках.

Решение. В этом испытании 36 равновозможных исходов. Случайная величина Х может принимать значения от 2 до 12, причём значения 2 и 12 она примет один раз, значения 3 и 11 – по 2 раза, значения 4 и 10 – по 3 раза, 5 и 9 – по 4 раза, 6 и 8 – по 5 раз, значение 7 – 6 раз. Следовательно, закон распределения данной случайной величины Х можно задать таблицей

Х	2	3	4	5	6	7	8	9	10	11	12
Р		2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36

57. Задача. В коробке 7 карандашей, из которых 4 – красные. Из коробки случайным образом достают 3 карандаша. Найти закон распределения случайной вели-чины X, равной числу красных карандашей в выборке.

Решение. В выборке из трёх карандашей может не оказаться ни одного красного карандаша, может появиться один, два или три карандаша. Следовательно случайная величина Х может принимать значения х₁ =0; х₂ =1; х₃ =2; х₄=3.

Находим вероятности этих значений = ;

; .

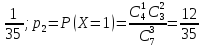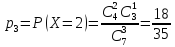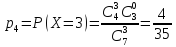Закон распределения примет вид:

X	0	1	2	3
P	1/35	12/35	18/35	4/35

58. Задача. Закон распределения дискретной случайной величины задан следующей таблицей.

X	0	1	2	3
P	0,2	0,4	0,3	0,1

Найти функцию распределения этой случайной величины.

Решение. Для построения функции распределения F(X) дискретной случайной величины Х воспользуемся формулой

1. При

2. При

3. При

4. При

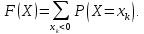
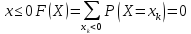
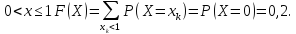
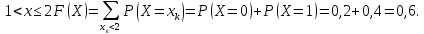
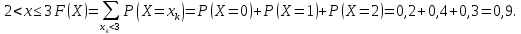
5. При

59. Задача. Случайная величина Х задана функцией распределения. 0 при x<0

F(x)= x/2 при 0<x<2

1 при x>2

Найти вероятность того, что в результате испытания случайная величина Х примет значение, заключённое в интервале [1,2].

Решение. Для данного интервала F(x)=x/2. Тогда по известным правилам P(1<X<2)=F(2)-F(1)=(2/2)-(1/2)=1/2

60. Задача. Случайная величина Х задана функцией распределения. 0 при x<0

F(x)= x/3 при 0<x<3

1 при x>3

Найти вероятность того, что в результате испытания случайная величина Х примет значение, заключённое в интервале [2,3].

Решение. По известным формулам для заданного интервала P(2<X<3)=F(3)-F(2)=(3/3)-(2/3)=1-2/3=1/3

61. Задача. Случайная величина Х задана функцией распределения. 0 при x<0

F(x)= sin x при 0<x<π/2