5. Методы преобразования данных
5.1. Нормировка значений признака
Некоторые методы обработки многомерных статистических данных требуют предварительной нормировки данных. Нормировка данных состоит в преобразовании данных к новой форме представления. Такие преобразования позволяют исключить влияние на результаты анализа принятых единиц измерения. Рассмотрим наиболее распространенные способы нормировки:
- центрирование;
- нормировка по максимальному значению;
- нормировка по минимальному значению;
- нормировка по среднему значению.
Приведем формулы для выполнения нормировок (5.1)-(5.4):
(5.1)
(5.2)
(5.3)
(5.4)
Рассмотрим пример выполнения нормировки признаков X и Y. Исходные значения признаков приведены на рис. 5.1.
Рис. 5.1. Исходные значения признаков X и Y
Результаты расчета параметров признаков X и Y приведены на рис. 5.2. Коэффициент корреляции равен -0, 62. Результаты выполнения операции нормировки приведены на рис. 5.3.
Рис. 5.2. Расчет параметров признаков X и Y
Рис. 5.3. Результаты нормировки признаков X и Y
Нормировка центрирование может быть выполнена с помощью функции EXCEL НОРМАЛИЗАЦИЯ (рис. 5.4).
Рис. 5.4. Функция EXCEL НОРМАЛИЗАЦИЯ
5.2. Преобразование измерительных шкал
Каждый метод многомерного статистического анализа разрабатывается для признаков, измеренных в определенной шкале измерений. Таблицы данных часто содержат признаки, измеренные в различных шкалах. Поэтому, чтобы применить определенный метод обработки к группе признаков необходимо привести их к единой шкале измерений. Преобразование признаков можно производить только с понижением мощности шкалы.
Преобразование непрерывного признака к ранговому представлению иначе называется операцией дискретизации. Такую операцию мы уже проделывали при расчете частотных рядов. Произведем эту операцию еще раз с данными, приведенными на рис. 5.4. Для выполнения операции потребуются данные по расчету таблицы параметров, которые приведены на рис.5.5.
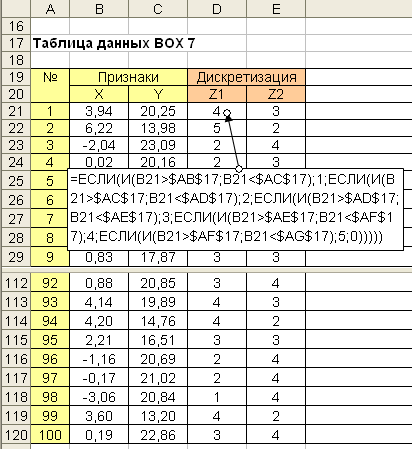
Рис. 5.4. Операция дискретизации
Рис. 5.5. Расчет параметров
Самой бедной шкалой
считается бинарная шкала. В этой шкале
признак может принимать только два
значения ноль или один (истина или ложь).
В некоторых задачах анализа, когда нужно
использовать самые разнообразные
признаки оказывается удобным привести
измерения к единой бинарной шкале.
Переход к бинарной шкале осуществляется
при ранговом или порядковом представлении
признака. Если какой-то признак представлен
в непрерывной шкале, то его всегда можно
привести к ранговому представлению с
помощью операции дискретизации. Будем
использовать ранговое представление
признаков из таблицы данных рис. 5.4. При
бинарном представлении каждому ранговому
признаку ставится в соответствие kбинарных признаков (k– количество
возможных различных значений рангового
признака). Бинарное представление
признаков X и Y приведено на рис. 5.6. Это
соответственно признаки
и
.
Преобразование производится по следующей
схеме. Если исходный ранговый признак
принимает значение ранга с номеромg,
то бинарный признак с номеромg принимает
значение 1, а все остальные компоненты
бинарного вектора принимают значение
0. Сумма значений бинарного вектора
будет равна 1. Например, если число
ранговых значенийg=5, то ранговое
значение 3 в бинарном представлении
будет иметь вид (0,0,1,0,0).
На рис. 5.6. представлены результаты преобразования признаков X и Y к бинарному виду. В столбцах таблицы данных V и W рассчитаны суммы значений по двум бинарным векторам. Соответственно суммы по столбцам V и W будут равны количеству наблюдений в таблице данных.
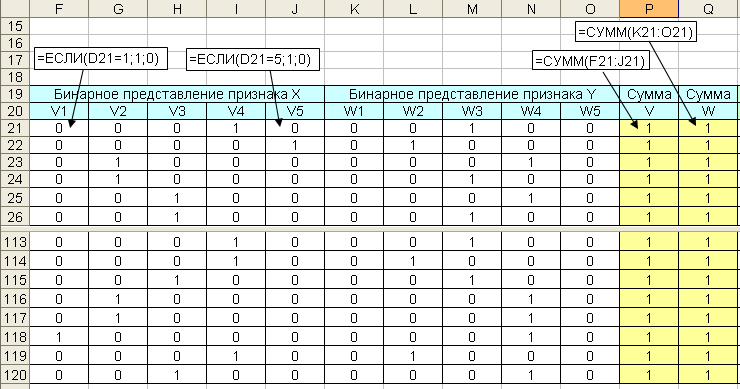
Рис. 5.6. Преобразование признаков к бинарному представлению