
- •МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ
- •1.ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) В ДВУМЕРНОМ СЛУЧАЕ
- •2. РЕШЕНИЕ ЗАДАЧ ТИПА ТРАНСПОРТНОЙ В MICROSOFT EXCEL, ИСПОЛЬЗУЯ НАДСТРОЙКУ «ПОИСК РЕШЕНИЯ»
- •3. РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ EXCEL ОДНОЙ ИЗ ЗАДАЧ ОПТИМИЗАЦИИ ПРИ СЕТЕВОМ ПЛАНИРОВАНИИ И УПРАВЛЕНИИ (СПУ)
- •4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- •5. БАЛАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА
- •6.МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ
- •ЛИТЕРАТУРА
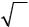
4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Если целевая функция либо система ограничений (либо вместе) содержит выражения, нелинейные по искомым переменным, то задача является задачей нелинейного программирования. Задачи, в которых ограничения и функция цели линейны и предполагается целочисленность переменных, также являются нелинейными. В задачах нелинейного программирования отсутствуют все или некоторые из свойств, характеризующих линейные задачи. Область допустимых решений в задачах линейного программирования выпукла. В задачах нелинейного программирования это свойство не сохраняется - областьдопустимых решений может быть невыпуклой либо даже состоять из нескольких несвязанных областей. Таким образом, в общем случае задача нелинейного программирования является чрезвычайно трудной для решения. Если число переменных в задаче не превышает трех, то можно попытаться решить задачу графически [3,6]. Графическое решение задачи нелинейного программирования существенно отличается от такого же решения задач линейного программирования. Даже в том случае, если область допустимых решений задачи представлена системой линейных неравенств, оптимальное решение задачи может находиться в любой точке области: на границеилидажевнутриобласти.
Примеры графического решения задач нелинейного программирова-
ния.
Пример1. Найтиоптимальноерешениезадачи
x1 + 2x2 ≤12 (I);
x1 + x2 ≤9 (II);
x1 ≥ 0; x2 ≥ 0;
f = (x − 2)2 + (x −3)2 → min/ max. |
|
|
|
|
1 |
2 |
|
|
|
Область |
допустимых решений (ОДР) задачи |
— четырехуголь- |
||
никOEBD , представленный на рис. 4.1. Линии уровня целевой функции — |
||||
концентрические окружности радиусом |
f ( f ≥ 0) с |
центром |
в точке |
|
A(2;3) , которая находится внутри ОДР; очевидно, что с ростом f |
радиус |
|||
окружности увеличивается. В точке A(2;3) |
достигается минимум целевой |
|||
функции, равный fmin =0. Максимальное значение целевой функции достигается на окружности, проходящей через точку D(9;0) , где fmax =(9 −2)2 +(0 −3)2 =58 .
33
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
fmax = 58 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
6 |
E |
|
|
|
|
|
|
|
|
3 |
A |
B |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
O |
2 |
9 |
D |
|
|
|
|
|
|
12 |
|
x1 |
|||
|
|
|
|
|
fmin |
= 0 |
|
|
I |
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
Рис.4.1. Графическое решение примера 1. |
|
|
|||
|
Пример 2. Найти оптимальное решение задачи |
|
|||||||
x + 2x |
≤12 (I); |
|
|
|
|
|
|||
|
1 |
2 |
|
|
|
|
|
|
|
x1 + x2 ≤9 (II); |
|
|
|
|
|
||||
x |
≥ 0; x |
2 |
≥ 0; |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
f |
= (x1 −7)(x2 −1) → min/ max. |
|
|
|
|
||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
6 |
E |
|
|
|
|
|
|
fm in |
= −35 |
|
B |
|
|
|
|
|
|
|
|
1 |
|
|
D |
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
7 |
9 |
12 |
x1 |
|
|
|
|
|
|
f m ax |
= 7 |
|
|
I |
|
|
|
|
|
|
II |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
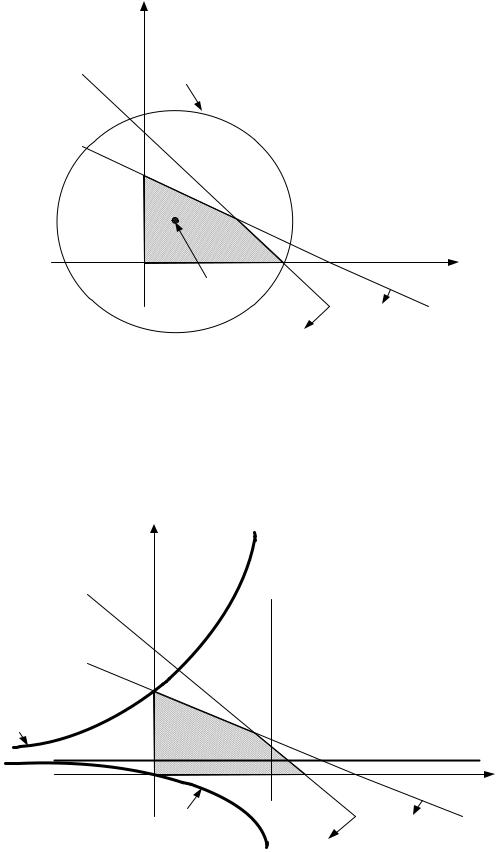
Рис.4.2. Графическое решение примера 2. |
|
||||
34
ОДРзадачитаже, чтоивпримере1— эточетырехугольник OEBD (рис. 4.2). Линиями уровня целевой функции являются гиперболы, асимптотами которых служат прямые x1 =7; x2 =1. С ростом модуля значения f гиперболы
удаляются от точки пересечения асимптот. Максимальное значение целевая функция достигает на гиперболе, проходящей через точку O(0;0) , где
fmax =7 . Наименьшее значение целевая функция достигает на гиперболе, проходящей через точку Е (0;6), где fmin = −35.
Отметим, что экстремум целевой функции (ЦФ) может достигаться в точке касания линии уровня ЦФ и граничной кривой ОДР. Для нахождения координат этой точки необходимо составить систему уравнений, включающую уравнения граничной кривой ОДР и линии уровня ЦФ, а также равенство угловых коэффициентов касательных к этим кривым в искомой точке касания.
Пример3. Найтиоптимальноерешениезадачи
x1 + 2x2 ≤12 (I);
x1 + x2 ≤9 (II);
x1 ≥ 0; x2 ≥ 0;
f = (x1 −4)2 +(x2 −9)2 → min/ max.
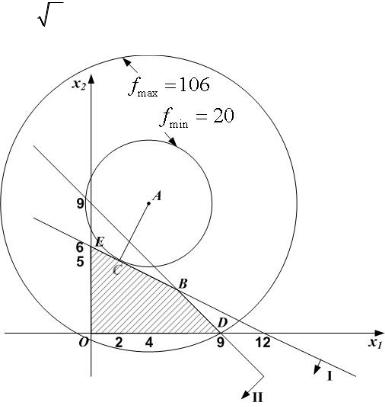
ОДР задачи та же, что и в примере 1 — это четырехугольник OEBD (рис.4.3). Линии уровня целевой функции — концентрические окружности
радиусом f ( f ≥ 0) с центром в точке A(4;9) , которая находится вне ОДР; очевидно, чтосростом f радиус окружности увеличивается.
Рис.4.3. Графическое решение примера 3.
35

Максимальное значение целевой функции достигается на окружности, про-
ходящей через точку D(9;0) , где fmax =(9 −4)2 +(0 −9)2 =106 . Минимальное значение целевой функции достигается на окружности, проходящей через точку C - точку касания этой окружности и граничного отрезка EB . Для нахождения координат точки C можно воспользоваться, по крайней мере, двумя способами. Первый – общий способ. Составляем систему уравнений, состоящую из 1) уравнения граничной прямой ограничения I , 2) выражения для ЦФ и 3) уравнения, отражающего равенство угловых коэффициентов граничной прямой ограничения I и касательной к линии уровня ЦФ. Угловой коэффициент граничной прямой ограничения I равен kI = −0,5 . Для нахождения углового коэффициента касательной к линии
уровня |
ЦФ |
|
в |
точке |
C |
вычислим |
|
производную |
от |
|
функции |
|||||||||||
x =9 − |
f −(x |
|
−4)2 , представляющей уравнение нижней (относительно |
|||||||||||||||||||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
x1 −4 |
|
|
||
точки |
A) части окружности. Эта производная равна |
= |
|
|
|
. |
||||||||||||||||
f −(x − |
4)2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x + |
2x |
|
=12; |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Итак, |
система уравнений имеет вид f |
= (x1 −4)2 +(x2 −9)2 ; |
|
|
Из вто- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
(x |
−4) |
|
f −(x |
−4)2 = −0,5. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рого уравнения системы выражаем f −(x |
|
−4)2 =(x −9)2 |
и |
подставляем в |
||||||||||||||||||
|
|
|
|
|
|
|
x1 −4 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||
третье; тогда получаем |
|
= −0,5 , т.к. |
|
| x |
|
−9 |=9 − x |
в силу того, |
что |
||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
9 − x2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
точка C расположена ниже точки A(4;9) . Итак, получаем систему линей- |
||||||||||||||||||||||
ных уравнений |
|
x + 2x =12; |
|
|
|
|
|
|
x = 2; |
определяет |
||||||||||||
|
1 |
2 |
|
|
|
Решение этой системы |
1 |
|
||||||||||||||
|
|
|
|
x1 −0,5x2 = −0,5. |
|
|
|
|
|
|
x2 =5 |
|
|
|
|
|||||||
координаты точки C(2;5) . Целевая функция принимает минимальное зна- |
||||||||||||||||||||||
чение в этой точке: |
fmin = f (C) =(2 −4)2 +(5 −9)2 = 20 . |
|
|
|
|
|
|
|
||||||||||||||
|
Во втором способе используем перпендикулярность радиуса AC и |
|||||||||||||||||||||
BE (касательной к окружности) в точке C . Угловой коэффициент BE ра- |
||||||||||||||||||||||
вен kI |
= −0,5 ; в силу перпендикулярности AC и BE угловой коэффициент |
|||||||||||||||||||||
прямой, |
содержащей AC , равен kAC = −1 kI = 2 . Тогда уравнение прямой, |
|||||||||||||||||||||
проходящей через точки A(4;9) |
и C , имеет вид x2 −9 = 2(x1 −4). Совмест- |
|||||||||||||||||||||
но с уравнением граничной прямой ограничения I оно образует систему |
||||||||||||||||||||||
x + 2x |
=12; |
решение которой |
x = 2; |
т.е. |
|
координаты точки |
C равны |
|||||||||||||||
1 |
2 |
|
1 |
|
|
|||||||||||||||||
2x1 − x2 = −1, |
|
|
|
|
|
|
x2 =5, |
|
|
|
|
|
|
|
|
|
|
|
||||
(2;5) . Целевая функция принимает минимальное значение в этой точке: fmin = f (C) =(2 −4)2 +(5 −9)2 = 20 .
36
Индивидуальные задания. Графически найти решение задачи нелинейного программирования.
Вариант 1. |
|
|
|
|
|
|
Вариант 2. |
|
|
|
|
|
|
|
|
|||||||
x |
+ 2x |
≤8; |
|
|
|
|
|
x |
+ |
2x |
≥ 2; |
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
3x1 + x2 ≤15; |
|
|
|
|
|
2x1 + x2 ≤11; |
|
|
|
|
|
|
||||||||||
x + x ≥1; |
|
|
|
|
|
x + x ≤ 6; |
|
|
|
|
|
|
|
|||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
x ≥ 0; x ≥ 0; |
|
|
|
|
|
x ≥ |
0; x ≥ 0; |
|
|
|
|
|
|
|
||||||||
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||
f |
= |
(x − |
6)2 + |
(x |
− 2)2 → min. |
f |
= (x − |
7)2 + (x |
|
−3)2 → min. |
||||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
Вариант 3. |
|
|
|
|
|
|
Вариант 4. |
|
|
|
|
|
|
|
|
|||||||
2x +3x |
|
≤13; |
|
|
|
|
9x +8x |
|
≤ 72; |
|
|
|
|
|
|
|||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
||
2x1 + x2 ≤10; |
|
|
|
|
|
x1 |
+ 2x2 ≤10; |
|
|
|
|
|
|
|
||||||||
x ≥ 0; x ≥ 0; |
|
|
|
|
|
x |
≥ |
0; x |
|
≥ 0; |
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||
f = |
2x − |
0,2x |
2 + |
3x |
2 |
− |
0,2x 2 → max. |
f =3x − |
0,3x |
2 |
+ |
6x |
|
−0,3x 2 |
→ max. |
|||||||
|
|
1 |
|
1 |
|
|
2 |
|
|
|
1 |
|
1 |
|
|
2 |
2 |
|
||||
Вариант 5. |
|
|
|
|
|
|
Вариант 6. |
|
|
|
|
|
|
|
|
|||||||
x + x ≤ 7; |
|
|
|
|
|
5x + 2x |
|
≥30; |
|
|
|
|
|
|
||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
x1 + 2x2 ≤10; |
|
|
|
|
|
3x1 + 4x2 ≤ 24; |
|
|
|
|
|
|
||||||||||
x |
≥ 0; x |
|
≥ 0; |
|
|
|
|
|
x |
≥ |
0; x |
|
≥ 0; |
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||
f =3x −0,2x 2 + x |
−0,2x 2 → max. |
f = 2x − |
0,1x |
2 |
+ |
3x |
|
−0,1x 2 |
→ max. |
|||||||||||||
|
|
1 |
|
1 |
|
2 |
|
|
2 |
|
|
|
1 |
|
1 |
|
|
2 |
|
2 |
|
|
Вариант 7. |
|
|
|
|
|
|
Вариант 8. |
|
|
|
|
|
|
|
|
|||||||
6x1 + 4x2 ≥12; |
|
|
|
|
x2 |
+ 2x |
+ x2 |
− 2x |
−14 ≥ 0; |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
|
|
2 |
|
|
|
2x1 + 3x2 ≤ 24; |
|
|
|
|
|
2x + x |
≤10; |
|
|
|
|
|
|
|||||||||
−3x1 + 4x2 ≤12; |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
≥ |
0; x |
|
≥ 0; |
|
|
|
|
|
|
|
|||||||
|
|
≥ 0; x |
|
≥ 0; |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
f |
= x1 x2 → max. |
|
|
|
|
|
|||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f |
= x1 x2 → max. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариант 9. |
|
|
|
|
|
|
Вариант 10. |
|
|
|
|
|
|
|
||||||||
3x1 + 2x2 ≥12; |
|
|
|
|
x2 |
− 2x |
+ x2 |
− 2x |
−34 ≤ 0; |
|
||||||||||||
|
|
− x ≤ 6; |
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
|
|
2 |
|
|
|
||
x |
|
|
|
|
|
|
x |
≥1; |
|
|
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 ≤ 4; |
|
|
|
|
|
|
|
x |
≥1; |
|
|
|
|
|
|
|
|
|
||||
|
|
≥ 0; x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
≥ 0; |
|
|
|
|
|
f |
= 4x1 + 3x2 → max. |
|
||||||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|||||||||||||
f |
= |
(x − |
5)2 + |
(x |
− 6)2 → min. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37
