
- •МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ
- •1.ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) В ДВУМЕРНОМ СЛУЧАЕ
- •2. РЕШЕНИЕ ЗАДАЧ ТИПА ТРАНСПОРТНОЙ В MICROSOFT EXCEL, ИСПОЛЬЗУЯ НАДСТРОЙКУ «ПОИСК РЕШЕНИЯ»
- •3. РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ EXCEL ОДНОЙ ИЗ ЗАДАЧ ОПТИМИЗАЦИИ ПРИ СЕТЕВОМ ПЛАНИРОВАНИИ И УПРАВЛЕНИИ (СПУ)
- •4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- •5. БАЛАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА
- •6.МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ
- •ЛИТЕРАТУРА

Учреждение образования Федерации профсоюзов Беларуси
Международный институт трудовых и социальных отношений
Витебский филиал
Факультет экономики и права
Кафедра Экономики и менеджмента
И.М.Котин
Экономикоматематические методы и модели
Учебно-методическое пособие по организации самостоятельной управляемой работы
для студентов дневного отделения экономических специальностей
Витебск, 2011
Печатается по решению научно-методического Совета ВФ УО ФПБ “МИТСО”
УДК 330.4 ББК 65в641
Автор - составитель: старший преподаватель кафедры экономики и менеджмента И.М. Котин
РЕЦЕНЗЕНТЫ:
М.Н.Борисевич, заведующий кафедрой компьютерного образования УО «ВГАВМ», к.ф.-м.н., доцент.
В.И.Иванов, доцент кафедры экономики и менеджмента ВФ УО ФПБ МИТСО, к.э.н.
Котин И.М.Экономико-математические методы и модели: учебнометодическое пособие по организации самостоятельной управляемой работы для студентов дневного отделения экономических специальностей, – Витебск: УО ФПБ МИТСО, 2011. – 48 с.
Пособие адресовано студентам экономических специальностей дневной формы обучения. Оно содержит задания для самостоятельного выполнения и поможет освоить отдельные темы, необходимые специалистам экономического профиля.
© Витебский филиал Учреждения образования Федерации профсоюзов Беларуси «Международный институт трудовых и социальных отношений»
2
СОДЕРЖАНИЕ |
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ........... |
4 |
1.ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ |
|
ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО |
|
ПРОГРАММИРОВАНИЯ (ЗЛП) В ДВУМЕРНОМ СЛУЧАЕ................... |
5 |
2. РЕШЕНИЕ ЗАДАЧ ТИПА ТРАНСПОРТНОЙ В MICROSOFT |
|
EXCEL, ИСПОЛЬЗУЯ НАДСТРОЙКУ «ПОИСК РЕШЕНИЯ» ............. |
22 |
3. РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ EXCEL ОДНОЙ ИЗ ЗАДАЧ |
|
ОПТИМИЗАЦИИ ПРИ СЕТЕВОМ ПЛАНИРОВАНИИ И УПРАВЛЕНИИ |
|
(СПУ) ..................................................................................................... |
27 |
4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО |
|
ПРОГРАММИРОВАНИЯ....................................................................... |
33 |
5. БАЛАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ МЕЖОТРАСЛЕВОГО |
|
БАЛАНСА. ............................................................................................. |
38 |
6.МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ.............................................. |
42 |
ЛИТЕРАТУРА........................................................................................ |
46 |
3
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ
Каждая самостоятельная работа имеет либо разобранный пример решения задания, либо подробные указания для выполнения задания. Перед тем, как приступить к решению заданий собственного варианта, необходимо внимательно ознакомиться с приведенными теоретическими сведениями и разобранными примерами.
Решение задания должно сопровождаться подробными пояснениями. В тех заданиях, где предусмотрено построение графиков, последние должны быть построены аккуратно, на осях системы координат должна обязательно присутствовать оцифровка. При возникновении затруднений при выполнении задания следует обратиться к процитированным литературным источникам.
Вариант задания выбирается по последней цифре номера зачетной книжки / студенческого билета (цифре 0 соответствует вариант №10). При выполнении задания не по своему варианту работа не будет рассмотрена.
4
1.ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) В ДВУМЕРНОМ СЛУЧАЕ
1. Теоретическое введение
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности ранее найденного оптимального решения. Для учета подобных ситуаций проводят анализ чувствительности оптимального решения ЗЛП., т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение ЗЛП [3,8].
Для решения задач анализа чувствительности ограничения линейной модели классифицируют следующим образом. Граничные прямые связывающих ограничений проходят через оптимальную точку. Граничные прямые несвязывающих ограничений не проходят через оптимальную точку. Аналогично “ресурс”, представляемый связывающим ограничением, называют дефицитным, а “ресурс”, представляемый несвязывающим ограничением – недефицитным. Слово “ресурс” взято в кавычки, поскольку ограничения ЗЛП могут быть обусловлены не только ограниченностью действительных ресурсов, но и другими экономическими требованиями рассматриваемой задачи, например, условиями реализации продукции на рынке. В дальнейшем будем иметь это в виду и кавычки опустим. Ограничение называют избыточным в том случае, если его исключение не влияет на область допустимых решений (ОДР) и, следовательно, на оптимальное решение. Выделяют, по крайней мере, три задачи анализа на чувствительность.
1.Анализ сокращения или увеличения ресурсов:
•на сколько можно изменить дефицитный ресурс для улучшения оптимального значения целевой функции (ЦФ)? Под улучшением оптимального значения ЦФ здесь понимается увеличение (уменьшение) этого значения в случае поиска максимума (минимума) ЦФ.
•на сколько можно изменить недефицитный ресурс (правую часть несвязывающего ограничения) при сохранении оптимального значения ЦФ?
2.Для какого из ресурсов изменение его “запаса” (т.е. правой части ограничения) наиболее выгодно?
3.Анализ изменения коэффициентов ЦФ: каков диапазон измене-
ния коэффициентов ЦФ, при котором не меняется оптимальное решение?
5
2. Методика графического анализа чувствительности оптимального решения
2.1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений).
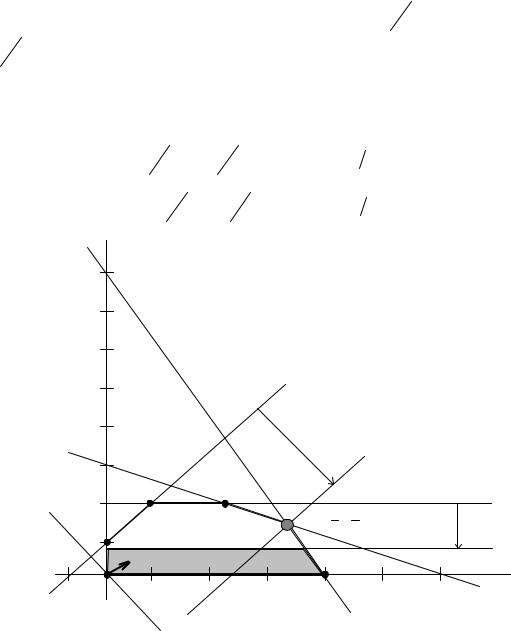
Проанализируем чувствительность оптимального решения задачи о производстве красок (см. Приложение 1, где поставлена эта задача и приведена ее математическая формулировка). ОДР задачи (рис.1.1) – многоугольник ABCDEF. В оптимальной точке Е пересекаются граничные прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты А и В) – дефицитными.
Рассмотрим экономический смысл этих понятий. Точка максимума
ЦФ Е соответствует суточному производству |
3 |
1 |
3 |
т краски 1-го вида и |
|||||||||||||
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
т краски 2-го вида. В производстве красок используются ингредиенты |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А и В. Суточный запас на складе ингредиентов А и В – это правые части |
|||||||||||||||||
связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим |
|||||||||||||||||
ограничениям, на производство в точке Е расходуется |
|
|
|||||||||||||||
|
|
|
|
1 3 1 |
3 |
+2 11 |
3 |
=6 |
|
т ингр.А сутки (1) и |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 3 13 +1 1 13 =8 |
[т ингр.В сутки] |
(2). |
|
||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
(2) |
|
|
|
|
|
|
L(X) =3x1 + 2x2 → max |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
7 |
|
|
|
|
|
|
|
|
x1 +2x2 ≤ 6, |
(1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2x |
+ x |
2 |
≤8, |
(2) |
||
|
|
6 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤1, |
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
−x1 + x2 |
||||||
|
|
5 |
|
|
|
|
|
(3) |
|
|
|
|
|
x2 |
≤ 2, |
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
x1 ≥ 0, x2 ≥ 0. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
C |
|
|
D |
|
|
E(31 |
;11) |
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
F |
|
|
|
|
(1) |
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
|
6 |
x1 |
|
|
|
|
|
|
L(X) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1.1. Графическое решение задачи о красках. |
||||||||||||||
6
Таким образом, понятие "связывающие ограничения" (1) и (2) озна- |
|||||||
чает, что при производстве красок в точке E (3 13 ;1 13 ) |
запасы ингредиен- |
||||||
тов А и В расходуются полностью и по этой причине невозможно даль- |
|||||||
нейшее наращивание производства. В этом заключается экономический |
|||||||
смысл понятия дефицитности ресурсов, т.е. если фабрика сможет увели- |
|||||||
чить суточные запасы ингредиентов, то это позволит увеличить выпуск |
|||||||
красок. В связи с этим возникает вопрос, до какого уровня целесообразно |
|||||||
увеличить запасы ингредиентов и на сколько при этом увеличится опти- |
|||||||
мальное производство красок? |
|
|
|
|
|||
|
|
|
Метода №1 |
|
|
||
Чтобы графически определить максимальное (по модулю) измене- |
|||||||
ние запаса дефицитного ресурса, вызывающее улучшение оптимального |
|||||||
решения, |
|
|
|
|
|
|
|
необходимо передвигать соответствующую граничную прямую па- |
|||||||
раллельно самой себе в направлении улучшения ЦФ до тех пор, пока это |
|||||||
ограничение не станет избыточным. |
|
|
|
||||
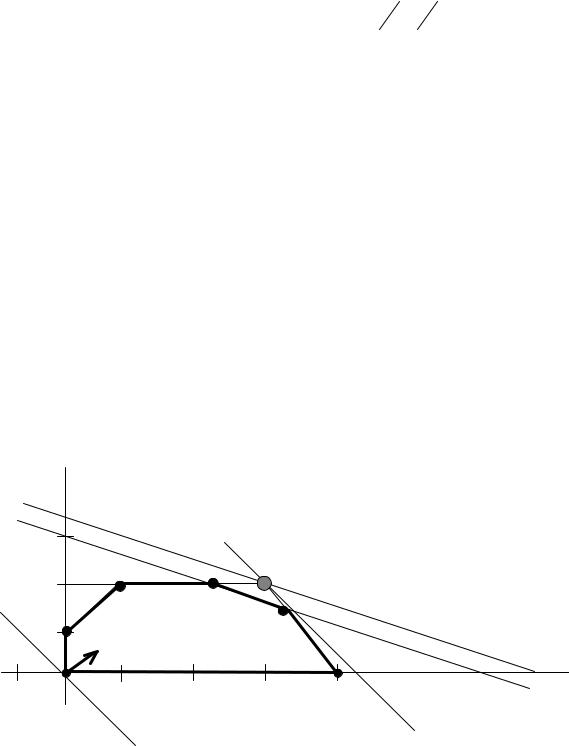
При прохождении прямой (1) через точку К (рис.1.2) многоугольник |
|||||||
ABCKF становится ОДР, а ограничение (1) – избыточным. Действительно, |
|||||||
если удалить прямую (1), проходящую через точку К, то ОДР ABCKF не |
|||||||
изменится. Точка К становится оптимальной, в этой точке ограничения (2) |
|||||||
и (4) становятся связывающими. |
|
|
|
|
|||
x2 |
|
|
|
|
|
|
|
3 |
|
|
|
К |
1x1 + 2x2 ≤ 6 |
(1) |
[т ингр.A/сутки] |
2 |
C |
|
|
|
|
|
|
(4) |
D |
|
|
|
|
|
|
1B |
(1) |
|
|
|
|
||
(3) |
|
E |
|
А=7 т |
|
||
А |
|
|
|
(2) |
F |
|
|
0 |
1 |
2 |
|
3 |
4 |
А=6 т |
x1 |
|
L(X) |
|
|
|
L(X) |
|
|
|
|
|
|
|
|
|
|
|
Рис.1.2. Анализ увеличения ресурса А. |
|
|||||
Метода №2
Чтобы численно определить новую величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения, необходимо:
7

1) определить координаты точки (x1; x2 ), в которой соответствующее огра- |
|||||||||
ничение становится избыточным; |
|
|
|
|
|
|
|||
2) подставить координаты |
(x1; x2 ) |
в левую часть соответствующего огра- |
|||||||
ничения; полученное значение и будет новой величиной исследуемого де- |
|||||||||
фицитного ресурса. |
|
|
|
|
|
|
|
||
Координаты точки К(3;2) находятся путем решения системы уравне- |
|||||||||
ний граничных прямых ограничений (2) и (4). Т.е. в этой точке фабрика |
|||||||||
будет производить 3 т краски 1-го вида и 2 т краски 2-го вида. Подставим |
|||||||||
x1 =3 и x2 = 2 в левую часть ограничения (1) и получим новую величину |
|||||||||
запаса ингредиента А |
|
|
|
|
|
|
|
||
|
|
x1 +2x2 =3 +2 2 =7 [т ингр.А/сутки]. |
|
|
|||||
Дальнейшее увеличение запаса ингредиента А нецелесообразно, по- |
|||||||||
тому что это не изменит ОДР и не приведет к другому оптимальному ре- |
|||||||||
шению (см. рис.1.2). Доход от продажи красок в объеме, соответствующем |
|||||||||
точке К, можно рассчитать, подставив ее координаты (3;2) в выражение |
|||||||||
ЦФ |
|
|
|
|
|
|
|
|
|
|
|
3x1 +2x2 =3 3 +2 2 =13 [тыс.руб./сутки]. |
|
||||||
Рассмотрим вопрос о целесообразности увеличения запаса ингреди- |
|||||||||
ента В. Согласно методе №1, соответствующее ограничение (2) становится |
|||||||||
избыточным в точке J, в которой пересекаются прямая (1) и ось перемен- |
|||||||||
ной x1 (рис.1.3). Многоугольник ABCDJ становится ОДР, а точка J(6;0) – |
|||||||||
оптимальным решением. |
|
|
|
|
|
|
|
||
x2 |
|
|
2x + x |
2 |
≤8 |
(2) |
[т ингр.В/сутки] |
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
B=8 т |
|
|
|
|
|
|
|
|
D |
|
|
|
B=12 т |
|
|
|
|
C |
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
||
|
(4) |
|
|
E |
|
|
|
|
|
1B |
|
(1) |
|
|
|
|
|
||
(3) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
(2) |
F |
|
J |
|
||
А |
|
|
|
|
|
|
|||
0 |
1 |
2 |
3 |
|
4 |
5 |
6 |
x1 |
|
|
|
L(X) |
|
|
|
|
|
|
L(X) |
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1.3. Анализ увеличения ресурса В. |
|
|
|||||
8

В точке J выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит
3x1 +2x2 =3 6 +2 0 =18 [тыс.руб./сутки].
Чтобы обеспечить такой режим работы, согласно методе №2, запас ингредиента В надо увеличить до значения
2x1 + x2 = 2 6 +0 =12 [т ингр.В/сутки].
Ограничения (3) и (4) являются несвязывающими, т.к. их граничные прямые не проходят через оптимальную точку E (см. рис.1.1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке E.
Например, увеличение (уменьшение) спроса на краску 2-го вида будет соответствовать перемещению прямой ограничения x2 ≤ 2 (4) вверх
(вниз). Перемещение прямой (4) вверх никак не может изменить точку Е максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой Е (см. Методу №3). Из рис.1.1 видно, что дальнейшее перемещение (4) приведет к тому, что точка Е будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки Е.
Метода №3
Чтобы определить максимальное изменение запаса недефицитного ресурса, не меняющее оптимальное решение,
необходимо передвигать соответствующую прямую параллельно са-
мой себе до пересечения с оптимальной точкой.
Метода №4
Чтобы численно определить новое значение запаса недефицитного ресурса, не меняющее оптимальное решение,
необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения; полученное значение и будет новой величиной исследуемого недефицитного ресурса.
Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке E(3 13 ;1 13), используем Мето-
ды №3 и №4. Подставляем в левую часть ограничения (4) координаты точки Е, получаем
x2 =1 13 .
9

Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность получен-
ного ранее решения, равен 1 13 т краски в сутки. Экономический смысл ограничения (3)
−x1 + x2 ≤1 [т краски сутки]
сутки]
втом, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки Е. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка Е остается оптимальной, является пересечение с точкой Е (см. рис.1.1). Согласно методе №4, подставим
координаты точки E(3 13 ;1 13) в левую часть ограничения (3)
−x1 + x2 = −3 13 +1 13 = −2 [т краски].
Получаем, что разность спросов на краску 2-го и 1-го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку Е означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1- го вида
x1 − x2 = 2 [т краски/сутки].
Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке Е не изменится, составляет 2 т краски в сутки.
Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.1.1.
10

Таблица 1.1
Результаты анализа ресурсов задачи №1
|
|
Max |
|
|
|
|
|
|
|
|
|
|
Max |
|
|
|
|
|
Ценность |
|
|
|
|
||||||||||||||
|
|
изменение |
|
|
|
|
|
|
|
|
|
|
|
|
дополнительной |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
изменение |
|
||||||||||||||||||||||||||||
|
|
модуля ре- |
|
|
|
|
|
|
|
единицы ресурса |
|||||||||||||||||||||||||||
№ |
Тип ресурса |
|
|
модуля дохода, |
|||||||||||||||||||||||||||||||||
сурса, |
|
|
|
|
|
|
|
max | |
L (X * ) |
| , |
y = |
max | |
L (X * )| |
, |
|||||||||||||||||||||||
|
|
max | Ri | , |
|
|
тыс.руб./сутки |
i |
|
max | |
R | |
|
|
|
|||||||||||||||||||||||||
|
|
т/сутки |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
тыс.руб./т |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
Дефицитный |
7-6=+1 |
|
|
|
|
|
|
|
13 −12 |
2 |
3 |
|
= |
1 |
3 |
|
|
1 |
3 |
|
= |
1 |
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y1 = |
|
1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(2) |
Дефицитный |
12-8=+4 |
|
|
|
|
18 −12 13 |
|
=5 13 |
y2 |
=[5 13 |
4] |
=1 13 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(3) |
Недефицитный |
-2-1= -3 |
|
|
|
|
|
12 2 |
3 |
−12 |
2 |
3 |
|
=0 |
y = 0 |
|
(| −3 |) = 0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(4) |
Недефицитный |
1 13 -2= −2 3 |
|
|
|
|
|
12 2 3 −12 2 3 |
|
=0 |
y4 = 0 |
( |
|
−23 |
|
) = 0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.2.Вторая задача анализа на чувствительность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Анализ табл.1 показывает, что к улучшению оптимального решения, |
|
|||||||||||||||||||||||||||||||||||
т.е. к увеличению суточного дохода приводит увеличение дефицитных ре- |
|
||||||||||||||||||||||||||||||||||||
сурсов. Для определения выгодности увеличения этих ресурсов использу- |
|
||||||||||||||||||||||||||||||||||||
ют понятие средней ценности дополнительной единицы i-го ресурса yi |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
y |
= |
max | |
|
|
L (X * )| |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
i |
|
|
max | Ri | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где max | L(X * )| – максимальное приращение модуля оптимального зна-
чения ЦФ; max | Ri | – максимально допустимый прирост модуля объема
i-го ресурса.
Например, из табл.1.1 следует, что увеличение суточного запаса ингредиента А [ограничение (1)] на 1 т позволит получить дополнительный
доход, равный y1 = 13 тыс.руб./сутки, в то время как увеличение запаса В
[ограничение (2)] на 1 т принесет y2 =1 13 тыс.руб./сутки. Недефицитные
ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.
Вывод: дополнительные вложения в первую очередь необходимо направлять на увеличение ресурса В, а лишь потом на ресурс А. Изменять недефицитные ресурсы нет необходимости.
11
2.3. Третья задача анализа на чувствительность
Графический анализ допустимого диапазона изменения коэффициентов целевой функции (цен)
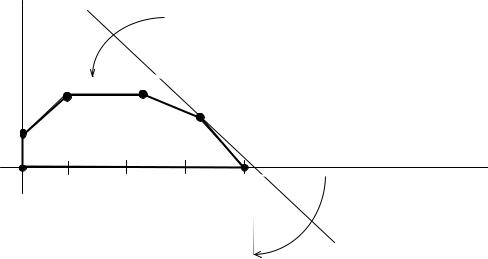
Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой (т.е. линии уровня ЦФ) вокруг оптимальной точки. Так, при увеличении коэффициента ЦФ c1
или уменьшении c2 целевая прямая вращается по часовой стрелке. При уменьшении c1 или же увеличении c2 целевая прямая вращается против
часовой стрелки (рис.1.4).
При таких поворотах точка Е будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами граничных прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка DE.
x |
2 |
|
|
уменьшение c |
|
||
|
|
|
|
1 |
|
||
|
|
|
|
|
или |
|
|
3 |
|
|
|
|
увеличение c2 |
|
|
|
|
C |
D |
|
|
|
|
2 |
|
|
|
L(X) =3x1 + 2x |
2 → max [тыс.руб./сутки] |
||
|
|
(4) |
(1) |
E |
|||
|
|
||||||
1B |
|
|
|
||||
|
(3) |
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
(2)F
0 А |
1 |
2 |
3 |
4 |
увеличение |
c |
x1 |
|
|
|
|
|
или |
1 |
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
уменьшение |
|
Рис.1.4. Анализ изменения цен.
При совпадении c прямой (2) оптимальным решением будут точки отрезка EF. Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно D или F.
Допустим, что цена на краску 2-го вида не меняется, т.е. зафиксируем значение целевого коэффициента c2 . Проанализируем графически ре-
зультаты изменения значения целевого коэффициент c1 , т.е. цены на крас-
ку 1-го вида. Оптимальное решение в точке Е не будет меняться при увеличении c1 до тех пор, пока целевая прямая не совпадет с прямой (2). Ана-
логично, оптимальное решение в точке Е не будет меняться при уменьшении c1 до тех пор, пока целевая прямая не совпадет с прямой (1).
12
Аналитический поиск допустимого диапазона изменения цен |
||
Совпадение в процессе вращения целевой прямой с прямой ограниче- |
||
ния означает, что углы их наклона относительно горизонтальной оси срав- |
||
нялись, а значит, стали равны тангенсы углов наклона этих прямых. |
||
|
Метода №5 |
|
Чтобы определить границы допустимого диапазона изменения ко- |
||
эффициента ЦФ, например min c1 и max c1 , |
||
необходимо приравнять тангенс |
угла наклона целевой прямой |
|
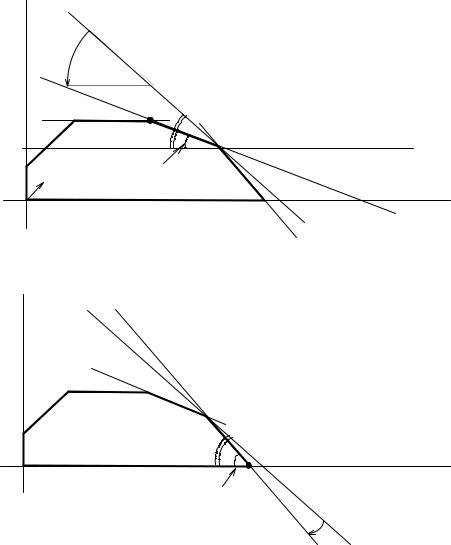
tgαЦФ поочередно к тангенсам углов наклона прямых связывающих огра- |
||
ничений, например tgα(1) и tgα(2) (рис.1.5 и 1.6). |
||
x2 |
L(X) |
c2 = const |
(1) |
уменьшение c1 |
|
|
|
|
(4) |
D |
|
|
αЦФ |
|
|
α(1) |
|
|
|
x1 |
|
(2) |
|
|
Рис.1.5. Определение min c1 . |
|
x2 |
|
|
|
(1) |
c2 = const |
|
|
|
|
αЦФ |
|
|
F |
x1 |
|
α(2) |
увеличение c1 |
|
|
L(X) |
|
|
(2) |
|
Рис.1.6. Определение max c1 . |
|
|
13 |
|
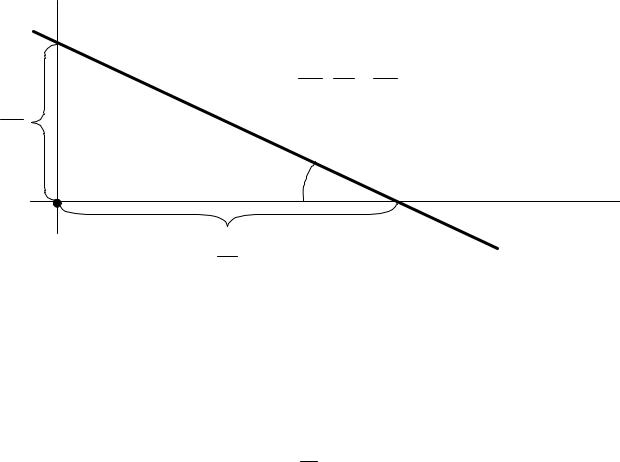
Определим насколько максимально может снизиться цена на краску |
|||||||
1-го вида, не изменяя оптимальную точку Е. Для этого применим Мето- |
|||||||
ду №5 и формулу расчета тангенса угла наклона прямой по отношению к |
|||||||
отрицательной полуоси OX1 (рис.1.7). |
|
|
|
|
|
||
x2 |
|
|
|
|
|
|
|
tgα = |
|
Z |
|
Y1 |
= Y1 |
||
|
|
|
Y |
|
Z |
Y |
|
Z |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
Y2 |
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
Y1x1 + Y2x2 = Z |
|
Y1 |
|
|
|
|
|
|
|
Рис.1.7. Определение тангенса угла наклона tgα прямой Y1x1 +Y2 x2 = Z . |
|||||||
Определим тангенсы углов наклона: |
|
|
|
|
|
|
|
1) целевой прямой L(X ) =3x1 +2x2 →max , учитывая, что c2 = 2 фик- |
|||||||
сировано |
|
= c1 |
= c1 |
|
|||
tgα |
ЦФ |
; |
|||||
|
|
|
c |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2) граничной прямой связывающего ограничения x1 +2x2 ≤6 (1) |
|||||||
tgα(1) = |
1 |
; |
|
||||
|
|
|
|
|
2 |
|
|
3) граничной прямой связывающего ограничения 2x1 + x2 ≤8 (2) |
|||||||
tgα(2) = |
2 |
= 2 . |
|
||||
|
|
|
|
1 |
|
|
|
Для нахождения minc1 целевая прямая должна совпасть с прямой (1) (см. |
|||||||
рис.1.5): |
|
|
|
|
|
|
|
tgαЦФ = tgα(1); |
|||||||
|
|
c1 |
|
= |
1 |
; |
|
|
|
2 |
|
|
2 |
|
|
min c1 =1 [тыс.руб./т]. |
|||||||
|
|
14 |
|
|
|
||
Для нахождения max c1 целевая прямая должна совпасть с прямой (2)
(см. рис.1.6):
tgαЦФ = tgα(2) ;
c21 = 2 ;
max c1 = 4 [тыс.руб./т].
Таким образом, если цены на краску первого вида будут колебаться в пределах 1<c1 < 4 тыс. руб./т (при цене на краску второго вида, равной
c2 = 2 тыс. руб./т), то оптимальное решение задачи не изменится.
Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс.руб./т ( c1 <1), то наиболее выгодным будет производство красок в точке D (см.
рис.1.5). При этом общее потребление ингредиента B снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и
(4).
15
ПРИЛОЖЕНИЕ 1
Задача
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы A и B на 1 т соответствующих красок (табл. П1). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
|
|
|
Таблица П1 |
|
Параметры задачи о производстве красок |
||
|
|
|
|
Ингредиен- |
Расход ингредиентов, т ингр./т краски |
Запас, |
|
ты |
Краска 1-го вида |
Краска 2-го вида |
т ингр./сутки |
А |
1 |
2 |
6 |
В |
2 |
1 |
8 |
Решение
Прежде чем построить математическую модель задачи, т.е. записать ее математически, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1)Что является искомыми величинами задачи?
2)Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?
3)Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию
ит.д.
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
16
1) Искомые величины являются переменными задачи, которые, как правило, обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде
X =(x1, x2 ,..., xn ).
2) Цель решения записывается в виде целевой функции (ЦФ), обозначаемой, например, L(X ). Математическая формула ЦФ L(X ) отражает
способ расчета значений параметра – критерия эффективности задачи.
3) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничений. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия.
В процессе записи математической модели необходимо указывать единицы измерения переменных задачи, целевой функции и всех ограничений.
Построим модель сформулированной задачи, используя описанную методику.
Переменные задачи
В задаче требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:
x1 – суточный объем производства краски 1-го вида, [т краски/сутки]; x2 – суточный объем производства краски 2-го вида, [т краски/сутки].
Целевая функция
В условии задачи сформулирована цель – добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи красок обоих видов, необходимо знать объемы производства красок, т.е. x1 и x2 т краски
в сутки, а также оптовые цены на краски 1-го и 2-го видов – согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен 3x1 тыс. руб. в сутки, а от продажи краски 2-го вида – 2x2 тыс. руб. в су-
тки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
L(X ) =3x1 +2x2 →max [тыс. руб./сутки],
|
тыс.руб. |
|
т краски |
= |
тыс.руб. |
|
|
. |
|||||
|
т краски |
|
сутки |
|
сутки |
|
17
Ограничения
Возможные объемы производства красок x1 и x2 ограничиваются следующими условиями:
•количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
•согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более чем на 1 т краски;
•объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;
•объемы производства красок не могут быть отрицательными. Таким образом, все ограничения задачи делятся на 3 группы, обу-
словленные:
1)расходом ингредиентов;
2)рыночным спросом на краску;
3)неотрицательностью объемов производства.
Ограничения по расходу любого из ингредиентов имеют следую-
щую содержательную форму записи
|
Расход конкретного ингредиента |
|
Максимально возможный |
|
|
≤ |
. |
|
на производство обоих видов краски |
|
запас данного ингредиента |
Запишем эти ограничения в математической форме.
Левая часть ограничения – это формула расчета суточного расхода
конкретного ингредиента на производство красок. Так из условия известен расход ингредиента А на производство 1 т краски 1-го вида (1 т ингр. А) и 1 т краски 2-го вида (2 т ингр. А) (см. табл.П1). Тогда на производство x1 т
краски 1-го вида и x2 т краски 2-го вида потребуется 1x1 +2x2 т ингр. А.
Правая часть ограничения – это величина суточного запаса ингреди-
ента на складе, например, 6 т ингредиента А в сутки (см. табл.П1). Таким образом, ограничение по расходу А имеет вид
1x |
+ 2x ≤ 6 |
|
т ингр.А |
|
т краски |
≤ |
|
т ингр.А |
. |
|
|
|
|
|
|
|
|||||
1 |
2 |
т краски |
|
сутки |
|
сутки |
|
|||
|
|
|
|
|
|
|
|
|||
Аналогична математическая запись ограничения по расходу В
2x |
+1x ≤8 |
|
т ингр.В |
|
т краски |
≤ |
|
т ингр.В |
. |
|
|
|
|
|
|
|
|||||
1 |
2 |
т краски |
|
сутки |
|
сутки |
|
|||
|
|
|
|
|
|
|
|
|||
Примечание 1. Следует всегда проверять размерность левой и правой части каждого из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибке при составлении ограничений.
18
Ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го вида имеет
содержательную форму
Превышение объема производства краски 2-го вида |
≤ 1 |
т краски |
|
|||||||
над объемом производства краски 1-го вида |
|
|
сутки |
|
||||||
|
и математическую форму |
|
|
|
|
|||||
x |
− x ≤1 |
|
т краски |
≤ |
|
т краски |
. |
|
|
|
|
|
|
|
|
|
|
||||
2 |
1 |
|
|
сутки |
|
|
|
|
||
|
|
|
сутки |
|
|
|
|
|
||
Ограничение по суточному объему производства краски 1-го вида
имеет
содержательную форму |
|
|||
|
|
т краски |
|
|
(Спрос на краску 1-го вида)≤ |
2 |
|
||
сутки |
||||
|
|
|
||
|
и математическую форму |
|
||||||
x |
≤ 2 |
|
т краски |
≤ |
|
т краски |
. |
|
|
|
|
|
|
||||
1 |
|
|
|
сутки |
|
|||
|
|
|
сутки |
|
|
|
||
Неотрицательность объемов производства задается как x1 ≥0, . x2 ≥0
Таким образом, математическая модель этой задачи имеет вид
L(X )=3x1 +2x2 →max [руб. сутки]
сутки]
x1 + 2x2 ≤ 6 |
[т ингр. A/сутки], |
|||
|
|
+ x2 |
≤8 |
[т ингр. B/сутки], |
2x1 |
||||
|
|
+ x2 |
≤1 |
[т краски сутки], |
−x1 |
||||
|
|
x2 |
≤ 2 |
[т краски сутки], |
|
|
|||
|
≥ 0, x2 |
≥ 0 |
[т краски сутки]. |
|
x1 |
||||
Ключевые понятия:
связывающие ограничения - ограничения, граничные прямые которых проходят через оптимальную точку; несвязывающие ограничения - ограничения, граничные прямые которых не проходят через оптимальную точку;
дефицитный ресурс – ресурс, представляемый связывающим ограничением;
19
недефицитный ресурс – ресурс, представляемый несвязывающим ограничением; избыточное ограничение – ограничение, исключение которого не влияет
на область допустимых решений задачи и, следовательно, на оптимальное решение;
средняя ценность дополнительной единицы i-го ресурса yi
y = |
max | |
L(X * )| |
, |
|
|
||
i |
max | Ri | |
|
|
|
|
||
где max | L(X * )| – максимальное приращение модуля оптимального зна-
чения ЦФ; max | Ri | – максимально допустимый прирост модуля объема i-го ресурса.
20
Индивидуальные задания. Найти графически решение задачи линейного программирования и исследовать его графически на чувствительность.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x1 + 4x2 ≥12; |
||||
|
3x + 2x ≥ 6; |
|
−4x + 2x ≤8; |
||||||||||||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
2 |
||
|
|
− x2 ≤1; |
|
|
|
x2 ≤ 6; |
|
||||||||||||
|
x1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
+5x2 ≤30; |
|
|
|
|
|
|
||||||||
G : 2x1 |
|
G : x1 + x2 ≤ 7; |
|||||||||||||||||
1. |
x |
+ x |
≤10; |
|
2. |
x |
≥1; |
|
|||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
x , x |
≥ 0. |
|
|
|
|
x ≤9; |
|
|||||||||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
L |
= |
x1 |
+ |
|
x2 |
→ |
max. |
|
x , x |
≥ 0. |
|||||||||
|
|
|
|
|
G |
|
|
|
1 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L = 2x |
+ x |
→max. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
G |
|
x1 − x2 ≤ 2; |
|
|
|
9x1 + 2x2 ≥18; |
||||||||||||||
|
|
|
|
x −3x ≤3; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
−7x1 + 2x2 ≤14; |
|
x1 ≤ 7; |
|
|||||||||||||||
|
|
|
|
≤10; |
|
|
|
|
|
|
|||||||||
G : x2 |
|
|
|
|
5. |
G : |
x + x ≤8; |
||||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
9x |
|
+7x |
≤ 63; |
|
1 |
|
2 |
|
||||||||||
|
|
|
|
x |
≤10; |
|
|||||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
x , x |
|
|
≥ 0. |
|
|
|
|
|
|
2 |
|
≥ 0. |
||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
x , x |
|||||
L = 2x |
+ x |
→max. |
|
|
1 |
2 |
|
|
|||||||||||
|
L = 2x + x |
→max. |
|||||||||||||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
G |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
G |
|
3x1 + 4x2 ≥12; |
|
−3x1 + 2x2 ≤ 6; |
||||||||||||||||
|
−7x + 4x |
≤ 28; |
|
2x −3x ≤ 6; |
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
1 |
|
2 |
|||
G : 8x1 +5x2 ≤ 40; |
|
G : 3x1 + x2 ≥3; |
|||||||||||||||||
7. |
x1 + x2 ≤9; |
|
|
8. |
x1 + x2 ≤ 4; |
||||||||||||||
|
3x −2x ≤9 |
|
|
x ≤5; |
|
||||||||||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
||
|
x , x ≥ 0. |
|
|
|
|
x , x ≥ 0. |
|||||||||||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
||
L = x + 2x |
→max |
. |
L = 2x + x |
→max. |
|||||||||||||||
|
|
|
1 |
|
|
|
|
2 |
|
G |
|
|
|
1 |
2 |
G |
|||
|
|
|
2x1 + x2 ≥ 4; |
|
|
|
|
|
|
||||||||||
|
|
|
x −4x |
|
≤ 4; |
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
G : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4x1 +5x2 ≤ 40; |
|
|
|
|
|
|
|||||||||||||
10. |
|
|
x |
|
+5x |
|
≤ 25; |
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x , x |
≥ 0. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
L = 2x |
|
+3x |
2 |
→max. |
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
G |
|
|
|
|
|
|
|||
|
−x + x |
|
≤ 2; |
|||
|
|
|
1 |
|
2 |
|
|
5x1 + 2x2 ≥10; |
|||||
|
G : 9x1 +8x2 ≤ 72; |
|||||
3. |
x1 −2x2 ≤ 2; |
|||||
|
x |
2 |
≤ 4; |
|
|
|
|
|
|
|
|
|
|
|
x , x ≥ 0. |
|||||
|
1 |
|
2 |
|
|
|
|
L = x |
+ |
2x |
→max. |
||
|
1 |
|
|
2 |
|
G |
10x1 + x2 ≥10;
2x1 −3x2 ≤ 6;
6. G : 8x1 +10x2 ≤80;
x1 + x2 ≤12;x1, x2 ≥ 0.
L = −3x1 − x2 G →min.
x1 + 2x2 ≥ 4;x1 − x2 ≤ 2;
9. G : 5x1 +7x2 ≤35;
x2 ≤ 6;x1, x2 ≥ 0.
L = −2x1 − x2 G →min.
21
