
- •МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЙ
- •1.ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) В ДВУМЕРНОМ СЛУЧАЕ
- •2. РЕШЕНИЕ ЗАДАЧ ТИПА ТРАНСПОРТНОЙ В MICROSOFT EXCEL, ИСПОЛЬЗУЯ НАДСТРОЙКУ «ПОИСК РЕШЕНИЯ»
- •3. РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ EXCEL ОДНОЙ ИЗ ЗАДАЧ ОПТИМИЗАЦИИ ПРИ СЕТЕВОМ ПЛАНИРОВАНИИ И УПРАВЛЕНИИ (СПУ)
- •4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- •5. БАЛАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА
- •6.МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ
- •ЛИТЕРАТУРА
3. РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ EXCEL ОДНОЙ ИЗ ЗАДАЧ ОПТИМИЗАЦИИ ПРИ СЕТЕВОМ ПЛАНИРОВАНИИ И УПРАВЛЕНИИ (СПУ)
Теоретические основы.
Одной из основных задач СПУ является нахождение на сетевом графике критического пути, длительность которого Tcr определяет время ис-
полнения всего проекта, описываемого с помощью СПУ [1,2]. Однако часто Tcr превосходит плановое время Tpl исполнения проекта. Использование
дополнительных ресурсов (денежных, трудовых, материальных и т.п.) приводит к сокращению сроков исполнения работ, входящих в проект:
tij' =tij −kij xij , где tij - время исполнения работы (i, j) в отсутствие дополнительных ресурсов, tij' - время исполнения работы (i, j) при использовании ресурсов в количестве xij , kij - технологические коэффициенты. Задача оп-
тимизации, связанная с подобным влиянием дополнительных ресурсов на длительности исполнения работ, состоит в следующем. Необходимо при минимальной затрате дополнительных ресурсов исполнить проект за время, не превосходящее плановое Tpl [4]. Математическая формулировка за-
дачи такова:
|
|
O |
≤T |
|
, (i,n) e; |
|
|
||||
T |
|
|
|
|
|||||||
|
in |
|
pl |
|
|
|
|
|
|
|
|
|
|
O |
|
H |
|
≥ dij , (i, j) e; |
|
|
|||
Tij |
−Tij |
|
|
|
|||||||
T O |
−T H |
|
=t |
ij |
−k |
x , (i, |
j) e; |
(3.1) |
|||
|
ij |
ij |
|
|
|
ij ij |
|
|
|||
T H ≥T O , (i, j,r) E; |
|
|
|||||||||
|
|
jr |
|
ij |
|
|
|
|
|
|
|
T H ≥ 0,T O ≥ 0, x ≥ 0, (i, j) e; |
|
||||||||||
|
|
|
|
|
|
ij |
|
|
ij |
|
|
ij |
|
|
|
|
|
|
|
||||
F = ∑xij |
→ min, |
|
(3.2) |
||||||||
|
|
|
(i, j) |
|
|
|
|
|
|
|
|
где e - множество работ проекта, |
E - множество событий проекта, n - за- |
||||||||||
вершающее событие проекта, TijO (TijH ) - момент окончания (начала) работы (i, j) , dij - минимально возможная длительность работы (i, j) .
Первое соотношение системы (3.1) означает, что все работы, оканчивающиеся в завершающем событии n , завершаются не позднее Tpl . Второе
соотношение указывает на то, что длительности всех работ не меньше минимальных длительностей этих работ. Третье соотношение дает зависи-
27
мость длительностей работ (i, j) от величины дополнительных ресурсов xij . Четвертое соотношение указывает на то, что все работы (i, j) , оканчивающиеся в некотором промежуточном узле j , имеют более ранние моменты окончания TijO , чем моменты TjrH начала работ ( j,r), исходящих из
этого же узла. Пятое соотношение отражает естественное условие неотрицательности рассматриваемых переменных (полагаем, что весь проект начинается в нулевой момент времени). Соотношение (3.2) представляет собой требование минимальности суммарных дополнительных затрат, т.е.
F = ∑xij - целевая функция задачи (3.1)-(3.2). Искомыми переменными
(i, j)
задачи (3.1)-(3.2) являются TijH ,TijO , xij , (i, j) e . Задача (3.1)-(3.2) является
задачей линейного программирования, для решения которой можно использовать симплекс-метод, либо численные методы. Поскольку даже при небольшом количестве работ в проекте, задача (3.1)-(3.2) имеет много искомых неизвестных, то эту задачу удобнее решать, например, в EXCEL с использованием надстройки «Поиск решения».
Пример решения задачи (3.1)-(3.2) в EXCEL
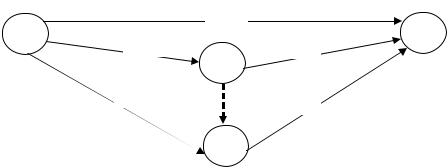
Рассмотрим проект, описываемый сетевым графиком, представленным на рис.3.1. Два числа у каждой дуги означают длительность работы без дополнительных ресурсов и минимальную длительность работы, т.е. tij
и dij соответственно. Плановое время исполнения проекта Tpl = 21, техно-
логические коэффициенты следующие: k12 =0,15;k13 =0,3;k14 =0,1;k24 =0,5;k34 =0,3.
|
|
10;6 |
1 |
14;8 |
4 |
|
4;3 |
|
|
|
2 |
20;12 |
12;7 |
|
3
Рис.3.1. Сетевой график проекта.
28
Оптимизационная задача имеет вид:
|
|
O |
|
|
|
O |
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T14 |
≤ 21;T24 ≤ 21;T34 |
≤ 21; |
|
|
−T H ≥ |
6;T O −T H ≥ |
0;T O −T H ≥3;T O −T H ≥ 7; |
||||||||||||||||||||||||
T O |
−T H |
≥8;T O |
−T H |
≥12;T O |
|||||||||||||||||||||||||||
|
12 |
|
12 |
|
|
13 |
|
|
13 |
|
|
|
14 |
|
14 |
|
|
23 |
|
23 |
|
24 |
24 |
34 |
34 |
||||||
|
|
O |
|
|
H |
|
|
|
|
|
|
|
|
|
O |
|
H |
+0,3x13 = 20; |
|
|
|
|
|
||||||||
T12 |
−T12 |
+0,15x12 =14;T13 −T13 |
|
|
|
|
|
||||||||||||||||||||||||
T14O |
−T14H +0,1x14 =10;T24O −T24H +0,5x24 = 4; |
|
|
|
|
|
|
(3.3) |
|||||||||||||||||||||||
|
|
|
−T H |
+0,3x |
|
=12; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
T O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
34 |
|
34 |
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
O |
|
|
H |
|
|
|
O |
|
|
H |
|
|
O |
|
H |
|
|
|
O |
|
|
H |
≤ 0; |
|
|
|
|||
T12 |
−T23 |
≤ 0;T12 |
−T24 |
≤ 0;T13 |
−T34 |
≤ 0;T23 |
−T34 |
|
|
|
|||||||||||||||||||||
|
|
O |
,T |
O |
,T |
O |
,T |
O |
,T |
O |
,T |
O |
,T |
H |
,T |
H |
,T |
H |
,T |
H |
,T |
H |
,T |
H |
≥ 0; |
|
|
|
|
||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
12 |
13 |
14 |
23 |
|
24 |
34 |
12 |
13 |
14 |
23 |
24 |
34 |
|
|
|
|
|
|
||||||||||||
x , x , x , x , x |
|
|
≥ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
12 |
13 |
14 |
24 34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
F = x12 |
+ x13 + x14 |
+ x24 + x34 →min. |
|
|
|
|
|
|
(3.4) |
|||||||||||||||||||
Итак, имеем 15 неизвестных и 18 ограничений, не считая ограничений неотрицательности неизвестных.
Методику задания данных в EXCEL для решения задачи линейного программирования можно почерпнуть, например, из [1]. Для решения в EXCEL задачи (3.3)-(3.4) в ячейки D4:T4 вносим значения 0 – это ячейки, значения в которых будут изменяться в процессе поиска решения. Эти значения соответствуют значениям искомых неизвестных, поименованных в ячейках D3:T3. В ячейки D5:T22 вносим коэффициенты из ограничений (3.3). В ячейки D23:T23 вносим коэффициенты целевой функции (3.4). В столбец U5:U23 помещаем формулы для нахождения левых частей ограничений (3.3) и выражения для целевой функции (3.4). Это делается следующим образом: в ячейку U5 помещаем формулу =СУММПРОИЗВ($D$4:$T$4;D5:T5), далее формула копируется до ячейки U23 включительно. Следует обратить внимание на то, что ячейки $D$4:$T$4 имеют абсолютную адресацию (почему?); абсолютная адресация задается либо вручную, либо нажатием клавиши F4. Отметим, что в ячейке U23 содержится выражение для целевой функции (3.4). В ячейки W5:W22 помещаем правые части ограничений (3.3). Столбец V5:V23 является информационным – в нем указаны соотношения между левыми и правыми частями ограничений (3.3). Лист EXCEL с введенными данными для задачи (3.3)-(3.4) приведен на рис.3.2.
На рис.3.3 представлена основная панель надстройки «Поиск решения» с введенными ограничениями задачи (3.3)-(3.4) и другими необходимыми для ее решения данными. Эта надстройка вызывается: в EXCEL 2003 - Сервис→Поиск решения; в EXCEL 2007 - Данные→Поиск решения.
Нажатие клавиши Выполнить приводит к сообщению о нахождении решения (см. рис.3.4); само решение задачи представлено на рис.3.5.
29
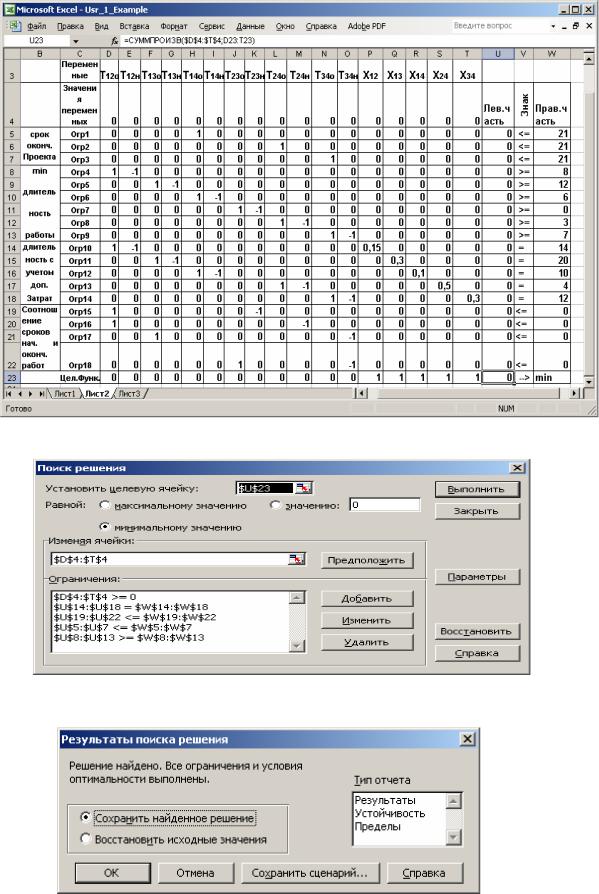
Рис.3.2. Лист EXCEL с введенными данными задачи (3.3)-(3.4). Курсор находится в ячейке U23 с выражением целевой функции.
Рис.3.3.Основная панель надстройки «Поиск решения» с ограничениями задачи (3.3)-(3.4) и другими необходимыми для ее решения данными.
Рис.3.4. Сообщение о найденном решении.
30

Рис.3.5. Решение задачи (3.3)-(3.4).
Итак, получили, что минимальные суммарные затраты ресурсов равны Fmin ≈36,67 , эти затраты распределены по работам следующим обра-
зом: x12 =0; x13 = 20; x14 =0; x24 =0; x34 ≈16,67 . Временные параметры работ таковы: T12H =0,T12O =14,T13H =0,T13O =14,T14H =0,T14O =10,T23H =14,T23O =14,
T24H =14,T24O =18,T34H =14,T34O = 21.
Индивидуальные задания.
Решить согласно варианту оптимизационную задачу СПУ с помощью EXCEL, предварительно выписав с использованием своих данных задачу (3.1)-(3.2). Сетевой график представлен на рис.3.6 (один для всех вариантов); данные по вариантам представлены в Таблице 3.1.
2
3
1 |
4 |
Рис.3.6. Сетевой график для индивидуального задания.
31
|
|
|
|
|
|
|
Таблица 3.1. |
|
Вариант |
Параметры |
|
|
Работа |
|
|
|
Tpl |
(1;2) |
(1;3) |
(1;4) |
(2;4) |
(3;4) |
|
|||
|
|
|
|
|||||
|
tij |
24 |
17 |
28 |
16 |
12 |
|
|
1 |
dij |
18 |
12 |
20 |
10 |
9 |
|
33 |
|
kij |
0,2 |
0,4 |
0,1 |
0,1 |
0,5 |
|
|
|
tij |
20 |
10 |
24 |
12 |
18 |
|
|
2 |
dij |
14 |
6 |
16 |
8 |
12 |
|
29 |
|
kij |
0,1 |
0,3 |
0,5 |
0,2 |
0,25 |
|
|
|
tij |
24 |
17 |
30 |
16 |
12 |
|
|
3 |
dij |
18 |
13 |
20 |
10 |
12 |
|
32 |
|
kij |
0,3 |
0,1 |
0,15 |
0,4 |
0,2 |
|
|
|
tij |
16 |
10 |
24 |
18 |
20 |
|
|
4 |
dij |
12 |
8 |
16 |
14 |
15 |
|
28 |
|
kij |
0,45 |
0,2 |
0,1 |
0,4 |
0,1 |
|
|
|
tij |
20 |
16 |
38 |
14 |
10 |
|
|
5 |
dij |
10 |
12 |
30 |
8 |
6 |
|
30 |
|
kij |
0,25 |
0,1 |
0,5 |
0,4 |
0,4 |
|
|
|
tij |
20 |
16 |
38 |
14 |
10 |
|
|
6 |
dij |
10 |
12 |
30 |
10 |
8 |
|
32 |
|
kij |
0,4 |
0,5 |
0,2 |
0,1 |
0,15 |
|
|
|
tij |
24 |
17 |
28 |
18 |
12 |
|
|
7 |
dij |
18 |
14 |
22 |
10 |
8 |
|
34 |
|
kij |
0,2 |
0,4 |
0,6 |
0,1 |
0,7 |
|
|
|
tij |
10 |
20 |
12 |
14 |
6 |
|
|
8 |
dij |
6 |
12 |
5 |
8 |
4 |
|
18 |
|
kij |
0,8 |
0,6 |
0,2 |
0,3 |
0,35 |
|
|
|
tij |
21 |
17 |
10 |
42 |
23 |
|
|
9 |
dij |
15 |
12 |
7 |
23 |
17 |
|
38 |
|
kij |
0,2 |
0,7 |
0,1 |
0,5 |
0,18 |
|
|
|
tij |
32 |
15 |
26 |
11 |
27 |
|
|
10 |
dij |
25 |
10 |
19 |
7 |
17 |
|
42 |
|
kij |
0,1 |
0,3 |
0,25 |
0,4 |
0,3 |
|
|
32
