Матричный метод анализа сетей Петри

Матричный метод основан на выражении (8.5), связывающим разметки сети, которые были до и после срабатывания некоторого перехода и матрице , описывающей работу сети.

Пусть начальная разметка сети равна . Если в сети допустима последовательность срабатывания переходов, то выполняются следующие соотношения

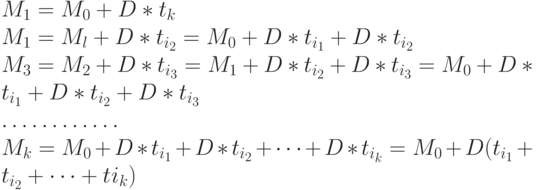
Обозначив ,получим

( 8.7)

Из-за того, что вектор тявляется суммой векторов вида (8.2) он должен быть целочисленным неотрицательным вектором. Выполнение соотношения (8.6) для некоторого целочисленного неотрицательного вектора является необходимым условием достижимости разметкииз началь-ной разметки.

Выражение (8.7) является системой линейных неоднородных уравнений относительно неизвестных компонент вектора . Следует заметить, что целочисленное неотрицательное решение уравнения (8.7), как правило, не определяет однозначно порядок срабатывания переходов, потому что от порядка суммирования вектороввида (8.2) суммане зависит. Для нахождения требуемого порядка срабатывания переходов необходимо проводить дополнительные исследования.

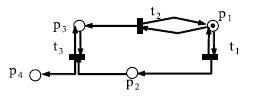
Рис. 8.9. Сеть Петри

Рассмотрим пример решения матричным методом задачи о достижимости. Спрашивается, достижима ли разметка для сети Петри, изображенной нарис.8.9?

Если разметка достижима, то указать последовательность срабатываний переходов, приводящую к данной разметке.

Матрица для данной сети Петри имеет вид

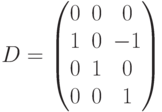
Матричное уравнение (8.6) для определения последовательности срабатываний переходов имеет вид

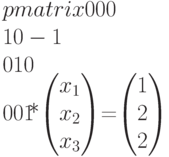
Без первого уравнения, которое тривиально выполняется, имеем систему трех уравнений с тремя неизвестными

Из второго и третьего уравнений получаем , а из первого. Таким образом, в качестве решения имеем целочисленный неотрицательный вектор

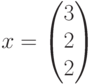
Этот вектор не определяет порядок срабатывания переходов. Среди последовательностей срабатывания есть невыполнимые, например, . Среди последовательностей срабатывания переходов, удовлетворяющих вектору, необходимо искать допустимые. Допустимых после-довательностей может быть много, а может и не быть вовсе. Для данного примера допустимой последовательностью является последовательностьили последовательность.

Наличие неотрицательного положительного решения у линейного уравнения для определения последовательности срабатывания является только необходимым условием и не гарантирует реального существова-ния такой последовательности. Например, решая задачу о достижимости разметки для описанной выше сети Петри, в качестве решения мы получим неотрицательный целочисленный вектор

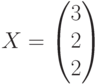
Однако реальной последовательности, приводящей к требуемой разметке, не существует, так как для срабатывания перехода необходимо наличие в местемаркера. Но фишка, попавшая в, не может покинуть эту позицию.

Пример 2 (решение матричным методом задачи о достижимости).

Рассмотрим сеть

Рис. .

и исследуем достижимость разметк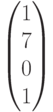и из начальной разметки

Матрица имеет вид

Матричное уравнение для определения последовательности срабатываний переходов имеет вид

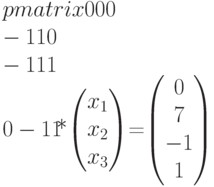
Без первого уравнения, которое тривиально выполняется, имеем систему

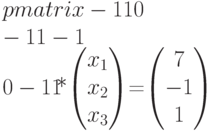
Складывая второе и третье уравнения, получим . Из первого уравнения получаем, а из третьего -. Таким образом, в качестве решения имеем целочисленный неотрицательный вектор

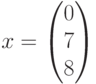
Этот вектор не определяет порядок срабатывания переходов. Среди последовательностей срабатывания есть невыполнимые, например

Среди последовательностей срабатывания переходов, удовлетворяющих вектору, необходимо искать допустимые. Допустимых последовательностей может быть много, а может и не быть вовсе. Для данного примера допустимой последовательностью является последовательность .

Матричный подход может быть использован для вектора весов, относительно которого сеть Петри является сохраняющей (консервативной). Пусть - вектор-строка искомых весов. В соответствии с приведенным выше определением консервативность сети заключается в выполнении равенства (8.6). Обе части этого равенства можно рассматривать как скалярные произведения векторана векторы любых двух достижимых разметок. Если в качестве одной из разметок взять начальную разметку, а в качестве второй - любую достижимую разметку, то из (8.6) следует, что. Из формулы (8.5) следует, что. В результате получаем, чтодля всех векторов, соответствующих достижимым разметкам. Равенство выполняется, если. Это матричное выражение представляет собой линейное однородное уравнение относительно весов, составляющих вектор.

Для сети, изображенной на рис.8.10, найдем матричным методом вектор весов, относительно которого она является сохраняющей. Эта сеть моделирует два взаимодействующих процесса обработки, использующих общий ресурс (описывается местом).

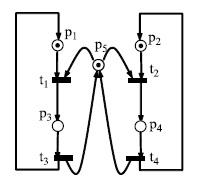
Рис. 8.10. Модель двух процессов, использующих неделимый ресурс

Матрица для данной сети имеет вид

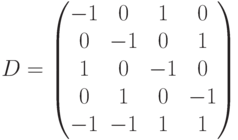
Легко заметить, что эта матрица имеет ранг 2 (третий столбец равен первому, умноженному на -1, а четвертый столбец равен второму, умноженному на -1). Поэтому система уравнений для вектора весоввключает в себя только два уравнения

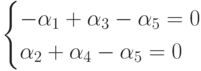
Существует бесконечно много решений этой системы, которые могут быть получены из выражений

при произвольном задании весов . Из этих выражений видно, что сеть не является строго сохраняющей, т. к. вектор (1, 1, 1, 1, 1) не является решением системы. В качестве вектора весов, относительно которого сеть является сохраняющей, нас интересуют только неотрицательные решения. Задавая, , получим. Вектор весов (1, 1, 1, 1, 0), являющийся решением системы, означает, что сеть сохраняет суммарное количество фишек во всех местах, за исключением места(количество фишек в местене учитывается при подсчете обще-го числа в сети). Еще одно решение (1, 1, 2, 2, 1) соответствует случаю, когда фишки в местахиучитываются при подсчете взвешенной суммы фишек в сети с коэффициентом 2.

Лекция 9