Оценки верхних границ корректирующих способностей кодов

Если расстояние между любыми двумя точками кода не меньше, чем , то шары радиусас центрами в кодовых словах не пересекаются. Поэтому общее число точек в этих шарах равно:, где- число точек (кодовых слов) в коде, ачисло точек в шаре радиуса. Так как число точек, попавших в шары, очевидно, не превосходит общего числа точек (двоичных слов) в, то. Это неравенство справедливо для любого множества с расстоянием между любыми двумя точками не меньше, чем, в том числе и для кода с максимальным числом слов, откуда и следует неравенство Хеминга.

Для максимального числа слов в коде, исправляющемошибок, может быть получена оценка снизу.

Утверждение(неравенство Варшамова - Гилберта):

Чтобы доказать неравенство Варшамова - Гилберта, можно рассмотреть следующую процедуру построения кода, исправляющего ошибок.

В качестве первого кодового слова возьмем произвольное слово (вектор) из . Рассмотрим шар радиусас центром в данном слове. Если весть слова, не вошедшие в этот шар, то в качестве второго кодового слова выберем любое из них. В качестве третьего кодового слова выберем любое слово, не вошедшее ни в один из построенных ранее шаров. Построим шар радиусас центром в данном слове. Продолжим эту процедуру выбора кодовых слов и построения шаров до тех пор, пока не будут исчерпаны все точки пространства. Предположим, построение кода завершилось зашагов. После завершения этой процедуры пространствобудет покрытопостроенными шарами, содержащими поточек каждый. Поскольку шары могут пересекаться, справедливо неравенство. Центры шаров образуют код, имеющий, как следует из способа построения, кодовое расстояние. Из того, что- это максимально возможное число точек кода с кодовым расстоянием не меньше, чем, следует, чтои. Последнее неравенство эквивалентно неравенству Варшамова - Гилберта.

Особенности векторных пространств над конечным полем gf(2). Линейный групповой код

Одним из подходов к регулярному построению кодов является применение в качестве кодовых множеств линейных подпространств [29],[33],[34]. Одно из преимуществ такого подхода заключается в хорошо изученной структуре подпространств линейных векторных пространств.

Для построения кодов, обнаруживающих и исправляющих ошибки, используются векторные пространства над конечным полем [32]. В этом случае множество (-мерный куб)рассматривается как линейное векторное пространство над конечным полем. Точки изстановятся векторами, их можно складывать и умножать на числа из поля.

Специфика некоторых понятий линейной алгебры в векторном пространстве является следствием особенностей поля. Сложение векторов изпроизводится покоординатно с учетом особенностей операции сложения в поле.

Сложение и умножение в поле определяется следующими таблицами.

Таблица сложения
	0		1
0	0		1
1	1		0
Таблица умножения
		0		1
0		0		1
1		0		1

Сложение в поле (сложение по модулю 2) часто обозначается. Этим же знаком будем обозначать сложение векторов из. Следует отметить справедливое для всех векторовравенство, вытекающее из таблицы сложения. Оно означает, что любой вектор является противоположным себе, а также что при заданныхи (уравнение имеет решение.

Рассмотрим особенности еще некоторых понятий линейной алгебры.

Линейная комбинацияв. Учитывая, чторассматривается как векторное пространство над конечным полем, содержащим только два элемента 0 и 1, линейная комбинация впревращается в сумму векторов

Линейная оболочкамножества векторов из- это совокупность различных сумм этих векторов. Линейная оболочка векторовбудет обозначаться через.

Линейная зависимостьвекторов из. Векторылинейно зависимы, если существует сумма некоторых из них, равная 0.

Векторы линейно независимы, если любая сумма некоторых из них не равна 0.

Утверждение. Если векторынезависимы, то все их линейные комбинации (суммы) различны.

Доказательство. Предположим, что Удалив из левой и правой частей этого равенства одинаковые векторы и перенеся оставшиеся из правой части в левую, получим нулевую сумму векторов. Это противоречит их линейной независимости.

Всего из линейно независимых векторов можно составить

линейных комбинаций, и все они различны.

Из доказанного утверждения следует, что линейная оболочка линейно независимых векторов содержитвектора.

Рассмотрим пример. Пусть имеем два вектора

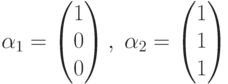
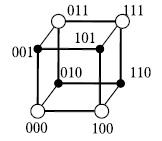
Их линейная оболочка состоит из четырех векторов На традиционном изображениив виде точек кубаобразуют плоскость (увеличенные светлые вершины куба на рисунке).

Подпространствав. Подпространством векторного пространстваназывается подмножество векторов из, замкнутое относительно операций сложения и умножения на число из поля. Линейная оболочкавекторовуявляется подпространством пространства.

Например, рассмотренная в предыдущем примере линейная оболочка из четырех векторов является подпространством, а множество векторов

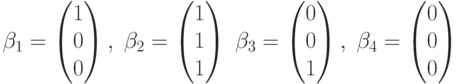
подпространством не является, поскольку оно не замкнуто относительно операции сложения. Например, не входит в это множество векторов.

По аналогии с подпространствами в подпространства вмогут задаваться системами линейных уравнений (но над полем). Именно таким образом далее будет задаваться линейный групповой код.

Нормой вектора называется числоединичных координат этого вектора. В кодировании норму вектора называют также весом этого вектора. С помощью нормы вектора и операции сложения векторов в(операции покоординатного сложения по) выражение для расстояния Хеминга может быть записано в виде

Кодовое расстояниелинейного кода может быть вычислено проще, чем кодовое расстояние произвольного кода. Учитывая, что для словлинейного кодасправедливо, выполняется следующая цепочка равенств

Определение. Пусть- матрица над полемразмераи ранга. Множестворешений уравненияназывается линейнымкодом.- проверочная матрица,- длина кода,- размерность кода. Если матрицаимеет вид, где- единичная матрица порядка, то код называется систематическим.