
- •Лекция 1 Основные понятия Об информационно-библиотечной культуре
- •Информация, сведения, данные, знания
- •Лекция 2 Неформальные и формальные каналы коммуникации
- •Библиотеки, библиография и библиографическое описание
- •Библиотечная и информационная деятельность
- •Тенденции развития основных видов документов
- •Закономерности роста и старения
- •Оценка значимости (влиятельности) ученых и журналов
- •Закон рассеяния статей конкретной тематики по журналам
- •Лекция 3 Предыстория и сущность
- •Процедуры и понятия
- •Координатное индексирование
- •Цитирование, библиографическое сочетание, социтирование
- •Рубрикаторы информационных изданий
- •Лекция 4 Электронные издания
- •Информационные ресурсы, структуры и инфраструктура
- •Информационные продукты и услуги
- •Лекция 5 Основные понятия и проблемы становления информационного общества. Информатизация как процесс перехода к информационному обществу
- •Возникновение, этапы развития и технологические аспекты информатизации
- •Положительные и отрицательные последствия информатизации
- •Программы информатизации
- •Программы информатизации России
- •Электронное правительство
- •Лекция 6 Представления информации Сообщение как материальная форма представления информации
- •Формы сообщений (сигналы, изображения, знаки, языковые сообщения)
- •Основные понятия теории формальных языков
- •Модели источников сообщений. Конечный вероятностный источник сообщений
- •Кодирование сообщений источника и текстов. Равномерное кодирование. Дерево кода
- •Неравномерное кодирование. Средняя длина кодирования
- •Префиксные коды
- •Необходимые и достаточные условия существования префиксного кода с заданными длинами кодовых слов. Неравенство Крафта
- •Методы построения кодов. Код Фано
- •Избыточность кодирования. Нижняя граница средней длины кодирования
- •Оптимальное кодирование, свойства оптимальных кодов, построение оптимальных кодов методом Хафмена
- •Лекция 7 Модель процесса передачи. Двоичный симметричный канал
- •Способы повышения надежности передачи сообщений
- •Принципы обнаружения и исправления ошибок с использованием кодов
- •Расстояние Хеминга и корректирующие возможности кодов
- •Оценки верхних границ корректирующих способностей кодов
- •Особенности векторных пространств над конечным полем gf(2). Линейный групповой код
- •Построение линейного кода по заданной порождающей матрице
- •Декодирование линейного кода по синдрому
- •Описание процесса обработки данных. Понятие алгоритма и его свойства. Способы формальной записи алгоритмов
- •Модель процесса обработки данных. Конечные автоматы
- •Сеть Петри как модель параллельно выполняемых процессов обработки
- •Формальное определение сети Петри
- •Основные задачи анализа процессов обработки, решаемые с использованием сетей Петри
- •Матричный метод анализа сетей Петри
- •Иерархия информационных систем управления Трансакционные системы
- •Системы бизнес-интеллекта
- •Аналитические приложения
- •Сущность erp-систем
- •Управление запасами и производством
- •Управление спецификациями изделий и технологиями производства
- •Планирование операций
- •Управление продажами
- •Управление запасами
- •Управление закупками
- •Управление производственными процессами
- •Учет и управление финансами Сущность финансового и управленческого учета
- •Главная книга
- •Расчеты с дебиторами
- •Расчеты с кредиторами
- •Основные средства
- •Денежные средства
- •Материально-производственные запасы
- •Расчеты с персоналом
- •Налоговый учет
- •Бухгалтерская отчетность
- •Аналитические возможности
- •Управление персоналом
- •Ограниченность erp-систем
- •Сущность систем бизнес-интеллекта
- •Хранилища данных Функциональность
- •Olap-системы Функциональность
- •Средства формирования запросов и визуализации данных Функциональность
- •Основные виды аналитических приложений
- •Системы управления эффективностью бизнеса (bpm-системы) Сущность концепции bpm
- •Функциональность bpm-систем
- •Управление по ключевым показателям Balanced Scorecard и другие методики управления по ключевым показателям
- •Функциональность bsc-систем
- •Корпоративное планирование и бюджетирование Основы корпоративного планирования и бюджетирования
- •Многомерное хранение информации
- •План счетов
- •Календарь планирования
- •Мультивалютность
- •Бизнес-правила
- •Описание финансовой структуры предприятия
- •Описание пользователей
- •Сценарии и версии
- •Управление процессом планирования
- •Формирование и анализ консолидированной финансовой отчетности Сущность консолидированной финансовой отчетности
- •Информационные системы консолидации финансовой отчетности
- •Аналитические направления
- •Сбор и структурирование исходной информации
- •Мультивалютность
- •Бизнес-правила
- •Журналы
- •Организация процесса консолидации
- •Процедуры консолидации
- •Bi-приложения
- •Системы финансового моделирования
- •Системы имитационного моделирования
- •Определения и термины
- •Области применения имитационных моделей
- •Последовательность разработки имитационных моделей
- •Компьютерная реализация имитационной модели
- •Система Arena
- •Экспертные системы
- •Архитектура экспертной системы
- •Классы экспертных систем
- •Технология создания экспертных систем
- •Рекомендации по выбору экспертной системы
- •Системы поддержки принятия решений
- •Определение систем поддержки принятия решений
- •Характеристика различных систем поддержки принятия решений
- •Выделение признаков классификации сппр
- •Особенности Экспертной системы поддержки принятия решений
- •Архитектура эсппр
- •Реализация выбора метода принятия решения в эсппр
- •Характеристика эсппр по выделенным признакам
- •Специализированные аналитические приложения
- •Принципы построения компьютера История и тенденции развития вычислительной техники
- •Основные характеристики и классификация компьютеров
- •Принципы построения компьютера
- •Структурные схемы и взаимодействие устройств компьютера
- •Компьютерные системы
- •Системы счисления
- •Перевод целых чисел
- •Перевод дробных чисел
- •Арифметические основы эвм Представление числовой информации в компьютере
- •Машинные коды
- •Арифметические операции над числами с фиксированной точкой
- •Логические основы эвм Основные сведения из алгебры логики
- •Законы алгебры логики
- •Техническая интерпретация логических функций
- •Кодирование информации в компьютере
- •Кодирование нечисловой информации
- •Кодирование текстовой информации
- •Кодирование графических данных
- •Кодирование звуковой информации
- •Основная память
- •Сверхоперативная память
- •Ассоциативная память
- •Центральный процессор эвм
- •Система команд микропроцессора
- •Взаимодействие элементов при работе микропроцессора
- •Системы визуального отображения информации (видеосистемы)
- •Клавиатура
- •Принтеры
- •Внешние запоминающие устройства (взу)
- •Накопитель на жестком магнитном диске
- •Оптические запоминающие устройства
- •Организация функционирования эвм с магистральной архитектурой
- •Организация работы эвм при выполнении задания пользователя
- •Особенности управления основной памятью эвм
- •Система прерываний эвм
- •Параллельные вычисления
- •Характеристика и особенности лкс
- •Протоколы и технологии локальных сетей
- •Сетевые устройства лкс
- •Структурированная кабельная система и логическая структуризация лкс
- •Виды глобальных сетей
- •Глобальные сети России РосНиирос
- •Магистральная сеть науки и образования rbNet (Russian Backbone Network)
- •Сеть runNet
- •Узел маршрутизации Российского фонда фундаментальных исследований (рффи)
- •Msk-IX (Московский центр взаимодействия компьютерных сетей Internet eXchange)
- •Сервисы Internet
- •Isp (Internet Service Provider)
- •Ipp (Internet Presence Provider)
- •Pcp (Private Content Publisher)
- •Характеристики хостинг-провайдеров
- •Программное обеспечение Интернета
Необходимые и достаточные условия существования префиксного кода с заданными длинами кодовых слов. Неравенство Крафта
Для применения кода на практике желательно, чтобы кодовые слова были как можно короче. Однако чем слова короче, тем их запас меньше. В этом легко убедиться, посмотрев на изображение словарного универсума на рис.6.3. Если попытаться построить префиксный код с очень короткими длинами кодовых слов, то можно потерпеть неудачу - кода с такими длинами слов может не быть. Например, нетрудно убедиться, что не существует префиксного кода с длинами слов 1, 1, 2. При необходимости построить префиксный код с большим числом кодовых слов заданной длины проверка существования такого кода может быть достаточно сложной. К счастью, найдены необходимые и достаточные условия на длины кодовых слов для существования префиксного и любого однозначно декодируемого кода. Эти условия известны как теорема Крафта - Макмиллана. Необходимые и достаточные условия сформулируем в виде двух теорем.
Теорема (необходимые
условия). Пусть
![]() -
префиксный двоичный код с длинами
кодовых слов
-
префиксный двоичный код с длинами
кодовых слов![]() .
Тогда выполняетсянеравенство
Крафта
.
Тогда выполняетсянеравенство
Крафта
|
|
( 6.3) |
Доказательство.
Рассмотрим, сколько слов длины
![]() может
быть в префиксном коде. Максимальное
число таких слов равно
может
быть в префиксном коде. Максимальное
число таких слов равно![]() .
В этом случае все
.
В этом случае все![]() кодовых
слова имеют длину
кодовых
слова имеют длину![]() .
.
Для каждого кодового
слова длины
![]() имеется
имеется![]() слов
длины
слов
длины![]() ,
для которых данное слово является
префиксом и по этой причине не является
кодовым. Это следует из структуры
словарного дерева (см. рис. 6.3). Множества
,
для которых данное слово является
префиксом и по этой причине не является
кодовым. Это следует из структуры
словарного дерева (см. рис. 6.3). Множества![]() и
и![]() слов
длины
слов
длины![]() ,
для которых кодовые слова
,
для которых кодовые слова![]() и
и![]() являются
префиксами, не пересекаются, так как в
противном случае более короткое из этих
слов было бы префиксом более длинного.
Значит, если в префиксном коде имеется
являются
префиксами, не пересекаются, так как в
противном случае более короткое из этих
слов было бы префиксом более длинного.
Значит, если в префиксном коде имеется![]() слов
длины
слов
длины![]() слов
длины
слов
длины![]() слов
длины 1, то число
слов
длины 1, то число![]() слов
длины
слов
длины![]() удовлетворяет
неравенству
удовлетворяет
неравенству
|
|
( 6.4) |
Это неравенство
верно для любого
![]() ,
в том числе и для
,
в том числе и для![]() ,
равного максимальной длине кодовых
слов. После деления на
,
равного максимальной длине кодовых
слов. После деления на![]() обеих
частей неравенства (6.4) его можно
преобразовать к виду
обеих
частей неравенства (6.4) его можно
преобразовать к виду
|
|
( 6.5) |
Слагаемое вида
![]() ,
представляющее в неравенстве (6.5)
,
представляющее в неравенстве (6.5)![]() кодовых
слов длины
кодовых
слов длины![]() ,
можно записать в виде суммы
,
можно записать в виде суммы
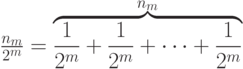
С учетом такого представления неравенство (6.5) можно переписать следующим образом:
![]()
где
![]() -
общее число словпрефиксного
кода. Теорема
доказана.
-
общее число словпрефиксного
кода. Теорема
доказана.
Выполнение неравенства Крафта доказано для префиксного кода. Однако в 1956 году Макмиллан доказал более общую теорему, согласно которой неравенство Крафта выполняется и для любого однозначно декодируемого кода. Доказательство теоремы изложено в [29], [31].
Можно также доказать, что если префиксный код полный, то в нестрогом неравенстве (6.3) будет выполняться равенство.
Теорема (достаточные
условия). Если положительные целые числа
![]() удовлетворяютнеравенству
Крафта
удовлетворяютнеравенству
Крафта
![]()
то существует
префиксный код
![]() с
длинами кодовых слов
с
длинами кодовых слов![]()
Доказательство.
Если среди чисел
![]() имеется
ровно
имеется
ровно![]() чисел,
равных
чисел,
равных![]() ,
тонеравенство
Крафта можно
записать в виде
,
тонеравенство
Крафта можно
записать в виде
![]()
где
![]() -
максимальное из данных чисел. Из
справедливости этого неравенства
следует, что верны неравенства (6.5) для
всех
-
максимальное из данных чисел. Из
справедливости этого неравенства
следует, что верны неравенства (6.5) для
всех![]() ,
а следовательно, и неравенство (6.4).
,
а следовательно, и неравенство (6.4).
Для построения
нужного префиксного
кода должна
быть возможность подходящим образом
выбрать
![]() слов
длины 1,
слов
длины 1,![]() слов
длины 2, вообще
слов
длины 2, вообще![]() слов
длины
слов
длины![]() или,
иными словами,
или,
иными словами,![]() вершин
кодового дерева на первом,
вершин
кодового дерева на первом,![]() -
на втором,
-
на втором,![]() -
на
-
на![]() -м
ярусе.
-м
ярусе.
Из неравенства
(6.4) при
![]() получаем
получаем![]() ,
т. е. требуемое число не превосходит
общего числа вершин первого яруса.
Значит, на этом ярусе можно выбрать
какие-то
,
т. е. требуемое число не превосходит
общего числа вершин первого яруса.
Значит, на этом ярусе можно выбрать
какие-то![]() вершин
в качестве концевых (
вершин
в качестве концевых (![]() равно 0, 1 или 2). Если это сделано, то из
общего числа вершин второго яруса (их
равно 0, 1 или 2). Если это сделано, то из
общего числа вершин второго яруса (их![]() )
для построения кода можно использовать
лишь
)
для построения кода можно использовать
лишь![]() .
Однако и этого числа вершин хватит, так
как из неравенства (6.4) при
.
Однако и этого числа вершин хватит, так
как из неравенства (6.4) при![]() вытекает
вытекает
![]()
Аналогично, при
![]() имеем
неравенство:
имеем
неравенство:
![]()
Правая часть его
вновь совпадает с допустимым для
построения префиксного
кода числом
вершин третьего яруса, если на первых
двух ярусах уже выбраны
![]() и
и![]() кодовых
вершин. Значит, снова можно выбрать
кодовых
вершин. Значит, снова можно выбрать![]() кодовых
вершин на третьем ярусе. Продолжая этот
процесс вплоть до
кодовых
вершин на третьем ярусе. Продолжая этот
процесс вплоть до![]() ,
мы и получим требуемый код. Теорема
доказана.
,
мы и получим требуемый код. Теорема
доказана.
Докажем, что если
для длин
![]() кодовых
слов выполняется равен - равенство
кодовых
слов выполняется равен - равенство![]() ,то
код является полным. Предположим
противное, то есть, что код не полный.
Тогда к нему можно добавить, по крайней
мере, одно кодовое слово (длины
,то
код является полным. Предположим
противное, то есть, что код не полный.
Тогда к нему можно добавить, по крайней
мере, одно кодовое слово (длины![]() )
и получить новыйпрефиксный
код, для которого,
с одной стороны,
)
и получить новыйпрефиксный
код, для которого,
с одной стороны,
![]() ,
а с другой стороны, в силу теоремы Крафта,
,
а с другой стороны, в силу теоремы Крафта,![]() Полученное
противоречие доказывает утверждение.
Полученное
противоречие доказывает утверждение.
Теоремы Крафта
доказаны для случая, когда рассматриваются
коды в алфавите
![]() .
Если кодовый алфавит содержит
.
Если кодовый алфавит содержит![]() символов,
то аналогичным образом можно доказать,
что необходимым и достаточным условием
для существованияпрефиксного
кода с длинами
слов
символов,
то аналогичным образом можно доказать,
что необходимым и достаточным условием
для существованияпрефиксного
кода с длинами
слов
![]() является
выполнение неравенства
является
выполнение неравенства
![]()
Оказывается, этому
неравенству обязаны удовлетворять и
длины кодовых слов произвольного
однозначно декодируемого кода. Поэтому,
если существует однозначно декодируемый
код с длинами слов
![]() ,
то существует ипрефиксный
код с теми же
длинами слов.
,
то существует ипрефиксный
код с теми же
длинами слов.
