Неравномерное кодирование. Средняя длина кодирования

В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.

Показателем экономичности или эффективности неравномерного кода является не длина отдельных кодовых слов, а "средняя" их длина, определяемая равенством:

где - кодовое слово, которым закодировано сообщение, а- его длина,- вероятность сообщения,- общее число сообщений источника. Для краткости записи формул далее могут использоваться обозначенияи. Заметим, что обозначение средней длины кодирования черезподчеркивает тот факт, что эта величина зависит как отисточника сообщений , так и от способа кодирования.

Наиболее экономным является код с наименьшей средней длиной . Сравним на примерах экономичность различных способов кодирования одного и того же источника.

Пусть источник содержит 4 сообщения с вероятностями. Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавитев соответствии с кодовой таблицей.

	00
	01
A_3	10
A_4	11

Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.

	0
	1
	10
	11

В этой таблице, в отличие от предыдущей, наиболее частые сообщения икодируются одним двоичным знаком. Для последнего варианта кодирования имеем

в то время как для равномерного кода средняя длина (она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.

При использовании неравномерных кодов появляется проблема, которую поясним на примере последней кодовой таблицы. Пусть при помощи этой таблицы кодируется последовательность сообщений , в результате чего она преобразуется в следующий двоичный текст: 010110. Первый знак исходного сообщения декодируется однозначно - это. Однако дальше начинается неопределенность:или. Это лишь некоторые из возможных вариантов декодирования исходной последовательности знаков.

Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.

Существо проблемы - в невозможности однозначного выделения кодовых слов. Для ее решения следовало бы отделить одно кодовое слово от другого. Разумеется, это можно сделать, но лишь используя либо паузу между словами, либо специальный разделительный знак, для которого необходимо особое кодовое обозначение. И тот, и другой путь, во-первых, противоречат описанному выше способу кодирования слов путем конкатенации кодов знаков, образующих слово, и, во-вторых, приведет к значительному удлинению кодового текста, сводя на нет преимущества использования кодов переменной длины.

Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).

Рассмотрим код (схему алфавитного кодирования) , заданный кодовой таблицей

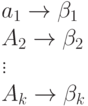
и различные слова, составленные из элементарных кодов.

Определение. Код называется однозначно декодируемым, если

и

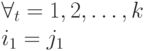
то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды.

Если таблица кодов содержит одинаковые кодовые слова, то есть если

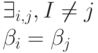
то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.