
- •Негосударственное образовательное учреждение высшего профессионального образования санкт-петербургский филиал росноу
- •Статистика
- •Раздел 1. Общая статистика 8
- •Раздел 2. Математическая статистика 70
- •Раздел 3. 107
- •Список использованной литературы……………………………...206 введение
- •Раздел 1. Общая статистика
- •Предмет и метод статистики. Источники статистической информации
- •1.1. Предмет, метод и задачи статистики
- •1.2. Статистическая информация
- •1.3. Закономерность и случайность
- •1.4. Статистические показатели
- •1.5. Способы представления закономерности
- •2. Современная организация государственной статистики. Источники статистической информации
- •2.1. Организация государственной статистики
- •2. 2. Источники статистической информации
- •2.3. Статистическое наблюдение
- •3.Статистическая сводка, метод группировок
- •3.1. Статистическая сводка
- •3. 2. Метод группировок
- •3.3. Ряды распределения
- •Основные аналитические показатели рядов динамики
- •4. Статистические таблицы. Статистические показатели и система статистических показателей
- •4.1. Статистические таблицы
- •Прогнозы цен сырьевых товаров
- •4. 2. Статистические показатели и система статистических показателей
- •5. Средние величины и показатели вариации
- •5. 1. Средние величины
- •5. 2. Понятие о моде и медиане
- •5. 3. Вариация признаков и способы ее измерения
- •Раздел 2.Математическая статистика
- •1. Обработка данных выборки
- •1. 1. Предмет математической статистики
- •1.2. Понятие о генеральной совокупности и случайной выборке
- •1. 3. Оценка надежности статистических характеристик
- •1.3.1. Определение числовых характеристик при малой выборке
- •1.3.2. Оценка надежности значенийи. Ошибка выборки.
- •1.4. Определение вида закона распределения случайной величины.
- •2. Установление закономерности развития процесса и прогнозирование
- •3. Статистическое изучение взаимосвязей
- •3.1. Вероятностные зависимости
- •3.2.Определение степени тесноты линейной зависимости параметрическим методом
- •3.2.1 Парная корреляция и парная регрессия
- •3.2.2. Множественная корреляция и множественная регрессия
- •3. 3. Непараметрический метод оценки связи
- •3.4. Внутригрупповая и межгрупповая вариация признака
- •4. Использование стандартных программ Excelдля решения прикладных задач
- •1. Средние величины и показатели вариации.
- •2. Построение гистограмм
- •3. Однофакторная аналитическая группировка
- •4. Метод наименьших квадратов
- •Раздел 3.
- •1.2. Агрегатный индекс
- •1.3. Агрегатный индекс количественных изменений
- •1.4. Агрегатный индекс качественных изменений
- •1.5. Основные соотношения между агрегатными индексами
- •1. 6.Средние индексы
- •1. 4. Ряды агрегатных индексов
- •2. Статистика труда
- •2. 1. Показатели численности работников
- •2.2. Характеристики затрат труда
- •3. Статистика производительности и оплаты труда
- •3.1. Производительность труда. Основные показатели и методы расчета
- •Изучение динамики производительности труда
- •Понятие о статистическом парадоксе
- •3.2. Производительность общественного труда
- •3.3. Статистика оплаты труда
- •4. Статистика себестоимости продукции
- •4.1. Задачи статистики себестоимости
- •4. 2. Методы изучения себестоимости продукции
- •4.3. Основные показатели и способы их расчета
- •4. 4. Пути снижения себестоимости
- •5. Статистика прибыли и рентабельности
- •3. Изменение рентабельности производства
- •6. Статистика доходов общества
- •6. 1. Оценка уровня и качества жизни населения
- •6. 2. Показатели доходов населения
- •6. З. Показатели потребления населением материальных благ. Понятие о прожиточном минимуме
- •6. 4. Статистика цен
- •7. Статистика торговли, общественного питания и научно-технического прогресса
- •7. 1. Статистика торговли
- •7. 2. Статистика общественного питания
- •7. 3. Статистика научно-технического прогресса.
- •8.Статистика социально-общественной эффективности общественного производства
- •8. 1. Статистика основных фондов
- •8. 2. Общественный продукт и его структура
- •8.3. Статистика продукции промышленности
- •8.4. Оценка качества продукции
- •Основные термины и определения
- •Тесты статистика
- •Вопрос 22. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 23. При изучении динамики изменения себестоимости продукции рассчитаны: индекс постоянного состава1,1; индекс структурных изменений1,2. В этом случае индекс переменного состава равен
- •Вопрос 24. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 26. Располагаемые доходы населения – это:
- •Список использованной литературы
3. Статистическое изучение взаимосвязей
3.1. Вероятностные зависимости
Исследуя экономические процессы, необходимо учитывать взаимозависимость различных факторов и уметь количественно оценить степень влияния одних факторов на другие. Оценка наиболее существенных причинно-следственных связей, а также воздействия одних факторов на другие является одной из основных задач статистики.
В школьном курсе изучают функциональные
зависимости,
школьном курсе изучают функциональные
зависимости,![]() ,
в которых каждому значениюх
соответствует определенное значение
у.
В экономике, опираясь на теорию
вероятностей, рассматривают вероятностные
зависимости, которые отражают, как в
среднем изменится у
при изменении х.
Например, на рисунке отражена вероятностная
зависимость, анализируя которую замечаем,
что при одном и том же значении х
значения у
могут быть совершенно разными, но, в то
же время, с увеличением х
значения у
в среднем увеличивается.
,
в которых каждому значениюх
соответствует определенное значение
у.
В экономике, опираясь на теорию
вероятностей, рассматривают вероятностные
зависимости, которые отражают, как в
среднем изменится у
при изменении х.
Например, на рисунке отражена вероятностная
зависимость, анализируя которую замечаем,
что при одном и том же значении х
значения у
могут быть совершенно разными, но, в то
же время, с увеличением х
значения у
в среднем увеличивается.
Если удается установить зависимость в среднем, то можно говорить о наличии связи между величинами. Чем больше разброс значение у при одном и том же значении х, тем слабее эта связь, чем меньше разброс значение у при одном и том же значении х, тем сильнее эта связь. В частном случае, когда каждому значению х соответствует только одно значение у, имеем функциональную зависимость.
Задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов: корреляционный анализ; регрессионный анализ.
Корреляционный анализ позволяет измерить силу связи между различными признаками и выделить факторы, оказывающие наибольшее влияние на результативный признак.
Регрессионный анализ позволяет установить форму зависимости, составить аналитическое уравнение, описывающее изменение процесса и тем обеспечить возможность прогнозирования.
3.2.Определение степени тесноты линейной зависимости параметрическим методом
3.2.1 Парная корреляция и парная регрессия
Величины бывают факторными и результативными, зависимыми и независимыми. Если случайных величин две, то говорят о парной зависимости результативной величины от факторной. Если случайных величин больше двух, то говорят о множественной зависимости результативной величины от нескольких факторных величин.
Зависимость между величинами может
быть более сильной или более слабой,
может быть функциональной, а может ее
и не быть вовсе. Очевидно, что силу связи
между величинами надо как-то измерять.
Для оценки связи между двумя случайными
величинами хиуиспользуется
числовая характеристика, которую в
теории вероятностей называюткорреляционный
моменти обозначают![]() .
В статистике его называют моментом
ковариации и обозначают –cov(xy).
Следовательно,
.
В статистике его называют моментом
ковариации и обозначают –cov(xy).
Следовательно,![]() =cov(xy).
=cov(xy).
По физическому смыслу корреляционный момент это математическое ожидание произведения центрированных случайных величин, т.е.
![]() .
.
Пример 3. 1. В результате опыта получены значения
|
|
1 |
2 |
3 |
4 |
5 |
|
|
3 |
5 |
7 |
9 |
11 |
Определить, являются ли зависимыми величины х и у.
Р е ш е н и е. 1. Находим средние значения х и у.
![]() .
. ![]() .
.
2. Рассчитываем
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
-4 |
-2 |
0 |
2 |
4 |
|
|
8 |
2 |
0 |
2 |
8 |
3. Вычисляем
![]() =
=![]() .
.
Выводы.
1.
![]() -
это значит, что связь междух
и у существует
(для независимых случайных величин
-
это значит, что связь междух
и у существует
(для независимых случайных величин
![]() ).
).
2.
![]() -
это значит, что связь положительная,
т.е. с увеличениемх
значение у
в среднем
возрастает.
-
это значит, что связь положительная,
т.е. с увеличениемх
значение у
в среднем
возрастает.
Как
видно из расчетной формулы, корреляционный
момент зависит от рассеивания. Чем
больше значения
![]() и
и![]() ,
тем больше значение
,
тем больше значение![]() .
Одной из характеристик рассеивания
является среднее квадратическое
отклонение. Чтобы избавиться от влияния
рассеивания на корреляционный момент
его делят на средние квадратические
отклонения. В результате имеем
.
Одной из характеристик рассеивания
является среднее квадратическое
отклонение. Чтобы избавиться от влияния
рассеивания на корреляционный момент
его делят на средние квадратические
отклонения. В результате имеем
![]() .
.
Полученное
значение
![]() называюткоэффициент
корреляции.
Коэффициент корреляции характеризует
степень тесноты линейной зависимости
между случайными величинами х
и у.
В отличии от корреляционного момента
значения коэффициента корреляции могут
изменяться от -1 до +1. Принято считать,
что если
называюткоэффициент
корреляции.
Коэффициент корреляции характеризует
степень тесноты линейной зависимости
между случайными величинами х
и у.
В отличии от корреляционного момента
значения коэффициента корреляции могут
изменяться от -1 до +1. Принято считать,
что если ![]() < 0,30, то связь
слабая; при
< 0,30, то связь
слабая; при ![]() = (0,3÷0,7) –
средняя; при
= (0,3÷0,7) –
средняя; при ![]() > 0,70 – сильная,
или тесная. Если
> 0,70 – сильная,
или тесная. Если![]() или
или![]() ,
то между случайными величинамих
и у
имеется линейная функциональная
зависимость. При этом, если
,
то между случайными величинамих
и у
имеется линейная функциональная
зависимость. При этом, если
![]() ,
то связь положительная, если
,
то связь положительная, если![]() ,
то связь отрицательная (знаки
,
то связь отрицательная (знаки![]() и
и![]() одинаковы). Если
одинаковы). Если![]() ,
то линейной вероятностной зависимости
между случайными величинамих
и у
не существует. Однако в этом случае
возможно нелинейное взаимодействие,
что требует дополнительной проверки и
других измерителей.
,
то линейной вероятностной зависимости
между случайными величинамих
и у
не существует. Однако в этом случае
возможно нелинейное взаимодействие,
что требует дополнительной проверки и
других измерителей.
Пример 3. 2. В условиях примера 1 определить коэффициент корреляции.
Р е ш е н и е. 1. Определяем значения средних квадратических отклонений:
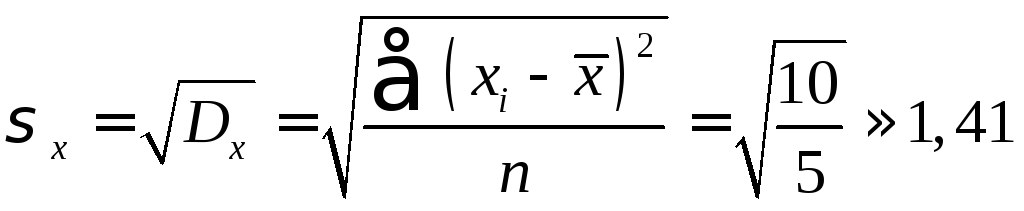 ;
; 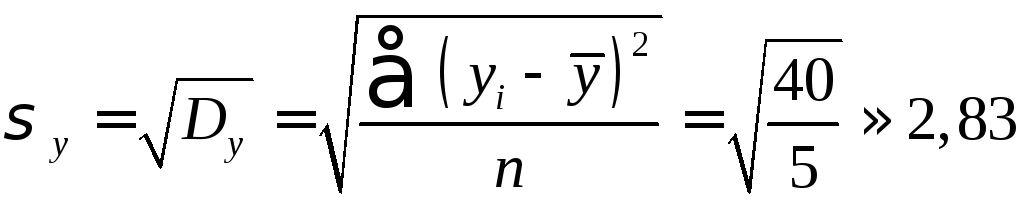
2.
Вычислим
![]() .
.
Выводы.
Между величинами х
и у
имеется линейная положительная
зависимость вида
![]() .
.
Порядок определения коэффициентов
![]() иbрассмотрен ранее.
иbрассмотрен ранее.
Напомним:
![]() ;
;![]() ,
где
,
где![]() .
.
Вычислим:
![]() .
.
|
Величины |
Значения |
Среднее значение | ||||
|
|
1 |
2 |
3 |
4 |
5 |
3 |
|
|
3 |
5 |
7 |
9 |
11 |
7 |
|
|
3 |
10 |
21 |
36 |
55 |
25 |
![]() .
.![]() .
.
Следовательно, уравнение регрессии имеет вид
![]() .
.
Пусть х= 3, тогда![]() ,
что соответствует исходным данным.
,
что соответствует исходным данным.
Выводы. 1 . Замечаем, как
![]() ,
так и
,
так и![]() ,
Это совпадение не случайное. Следовательно,
значение корреляционного момента можно
рассчитывать по любой из формул :
,
Это совпадение не случайное. Следовательно,
значение корреляционного момента можно
рассчитывать по любой из формул :
![]() или
или
![]() .
.
2.
Угол наклона линии регрессии равен ![]() .
.
3. Коэффициент kпоказывает, на сколько в среднем изменитсяу, при изменениехна одну единицу.
4.
При
![]() ,
значение
,
значение![]() .
.
В рассмотренных примерах присутствовали две случайные величины х и у. Связь двух признаков принято называть парной. Если рассматривается более двух переменных, говорят о множественной связи и описывают ее уравнением множественной регрессии.
Парная корреляция или парная регрессия могут рассматриваться как частный случай отражения связи одной из множества независимых переменных.
