- •Негосударственное образовательное учреждение высшего профессионального образования санкт-петербургский филиал росноу
- •Статистика
- •Раздел 1. Общая статистика 8
- •Раздел 2. Математическая статистика 70
- •Раздел 3. 107
- •Список использованной литературы……………………………...206 введение
- •Раздел 1. Общая статистика
- •Предмет и метод статистики. Источники статистической информации
- •1.1. Предмет, метод и задачи статистики
- •1.2. Статистическая информация
- •1.3. Закономерность и случайность
- •1.4. Статистические показатели
- •1.5. Способы представления закономерности
- •2. Современная организация государственной статистики. Источники статистической информации
- •2.1. Организация государственной статистики
- •2. 2. Источники статистической информации
- •2.3. Статистическое наблюдение
- •3.Статистическая сводка, метод группировок
- •3.1. Статистическая сводка
- •3. 2. Метод группировок
- •3.3. Ряды распределения
- •Основные аналитические показатели рядов динамики
- •4. Статистические таблицы. Статистические показатели и система статистических показателей
- •4.1. Статистические таблицы
- •Прогнозы цен сырьевых товаров
- •4. 2. Статистические показатели и система статистических показателей
- •5. Средние величины и показатели вариации
- •5. 1. Средние величины
- •5. 2. Понятие о моде и медиане
- •5. 3. Вариация признаков и способы ее измерения
- •Раздел 2.Математическая статистика
- •1. Обработка данных выборки
- •1. 1. Предмет математической статистики
- •1.2. Понятие о генеральной совокупности и случайной выборке
- •1. 3. Оценка надежности статистических характеристик
- •1.3.1. Определение числовых характеристик при малой выборке
- •1.3.2. Оценка надежности значенийи. Ошибка выборки.
- •1.4. Определение вида закона распределения случайной величины.
- •2. Установление закономерности развития процесса и прогнозирование
- •3. Статистическое изучение взаимосвязей
- •3.1. Вероятностные зависимости
- •3.2.Определение степени тесноты линейной зависимости параметрическим методом
- •3.2.1 Парная корреляция и парная регрессия
- •3.2.2. Множественная корреляция и множественная регрессия
- •3. 3. Непараметрический метод оценки связи
- •3.4. Внутригрупповая и межгрупповая вариация признака
- •4. Использование стандартных программ Excelдля решения прикладных задач
- •1. Средние величины и показатели вариации.
- •2. Построение гистограмм
- •3. Однофакторная аналитическая группировка
- •4. Метод наименьших квадратов
- •Раздел 3.
- •1.2. Агрегатный индекс
- •1.3. Агрегатный индекс количественных изменений
- •1.4. Агрегатный индекс качественных изменений
- •1.5. Основные соотношения между агрегатными индексами
- •1. 6.Средние индексы
- •1. 4. Ряды агрегатных индексов
- •2. Статистика труда
- •2. 1. Показатели численности работников
- •2.2. Характеристики затрат труда
- •3. Статистика производительности и оплаты труда
- •3.1. Производительность труда. Основные показатели и методы расчета
- •Изучение динамики производительности труда
- •Понятие о статистическом парадоксе
- •3.2. Производительность общественного труда
- •3.3. Статистика оплаты труда
- •4. Статистика себестоимости продукции
- •4.1. Задачи статистики себестоимости
- •4. 2. Методы изучения себестоимости продукции
- •4.3. Основные показатели и способы их расчета
- •4. 4. Пути снижения себестоимости
- •5. Статистика прибыли и рентабельности
- •3. Изменение рентабельности производства
- •6. Статистика доходов общества
- •6. 1. Оценка уровня и качества жизни населения
- •6. 2. Показатели доходов населения
- •6. З. Показатели потребления населением материальных благ. Понятие о прожиточном минимуме
- •6. 4. Статистика цен
- •7. Статистика торговли, общественного питания и научно-технического прогресса
- •7. 1. Статистика торговли
- •7. 2. Статистика общественного питания
- •7. 3. Статистика научно-технического прогресса.
- •8.Статистика социально-общественной эффективности общественного производства
- •8. 1. Статистика основных фондов
- •8. 2. Общественный продукт и его структура
- •8.3. Статистика продукции промышленности
- •8.4. Оценка качества продукции
- •Основные термины и определения
- •Тесты статистика
- •Вопрос 22. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 23. При изучении динамики изменения себестоимости продукции рассчитаны: индекс постоянного состава1,1; индекс структурных изменений1,2. В этом случае индекс переменного состава равен
- •Вопрос 24. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 26. Располагаемые доходы населения – это:
- •Список использованной литературы
1.4. Определение вида закона распределения случайной величины.
Вернемся к исходной таблице рассматриваемого примера, добавив еще одну строку в которой проставим частость одинаковых ответов
|
Размер, |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
Количество,
|
1 |
3 |
4 |
5 |
4 |
2 |
1 |
20 |
|
Частость,
|
0,05 |
0,15 |
0,2 |
0,25 |
0,2 |
0,1 |
0,05 |
1,00 |
П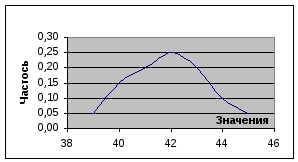 редставим
имеющиеся данные в виде графика. Как
видно из графика: - численные значения
изменяются не беспредельно; - чем больше
отклонение от среднего значения, тем
меньше частость ее появления и наоборот.
Следовательно, имеют место элементы,
присущие нормальному закону.
редставим
имеющиеся данные в виде графика. Как
видно из графика: - численные значения
изменяются не беспредельно; - чем больше
отклонение от среднего значения, тем
меньше частость ее появления и наоборот.
Следовательно, имеют место элементы,
присущие нормальному закону.
Выдвигаем гипотезу (Высказываем предположение): случайные величины распределены по нормальному закону. Но нормальный закон характерен для генеральной совокупности, а у нас выборка ограниченного объема. Насколько приемлема наша гипотеза?
Вполне очевидно, что при нормальном
законе распределения частости будут
иные. Если они отличаются от опытных
данных несущественно, то можно согласиться
с выдвинутой гипотезой, если отличия
существенные, то придется опровергнуть
гипотезу. Но что значит «несущественно»?
Видимо придется установить какой-либо
критерий. Существуют различные способы
установления критерия, который принято
называть «Критерий согласия». К числу
наиболее распространенных способов
относятся: критерий согласия Пирсона
![]() (
хи – квадрат); Романовского; Колмагорова
и Ястремского.
(
хи – квадрат); Романовского; Колмагорова
и Ястремского.
Сущность всех способов одинакова и
сводится к определению опытного значения
критерия согласия и сравнению его с
некоторым теоретическим значением.
Если опытное значение критерия согласия
превосходит теоретическое его значение,
то гипотеза отвергается, если не
превосходит, то принимается. Наиболее
распространенным является критерий
согласия Пирсона
![]() (
хи – квадрат). Рассмотрим порядок
проведения расчетов при использовании
этого способа.
(
хи – квадрат). Рассмотрим порядок
проведения расчетов при использовании
этого способа.
Формулируем основную гипотезу: опытное
распределение соответствуют теоретическому
распределению, что записывается в виде
![]() .
Тогда конкурирующая гипотеза
.
Тогда конкурирующая гипотеза![]() .
.
Опытное значение критерия согласия
рассчитывают по формуле
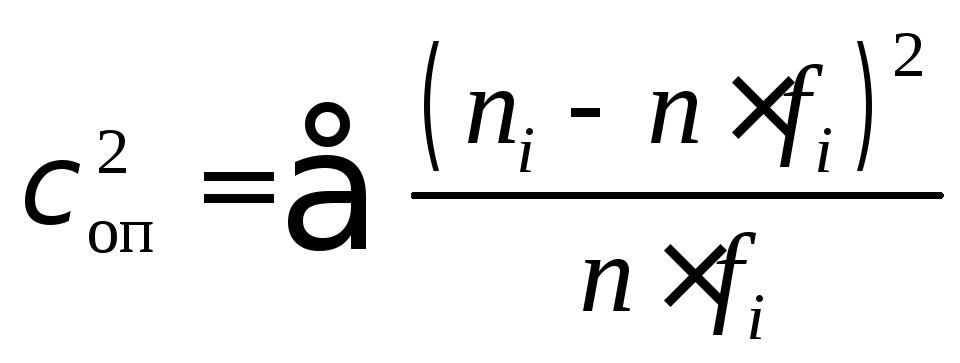 ,
,
|
где |
n |
– общее число опытов; |
|
|
|
– число значений, оказавшихся в i–м интервале по результатам опыта; |
|
|
|
– теоретическая частость попадания в i–ый интервал; |
|
|
|
– число значений в i–м интервале, которое соответствует теоретическому распределению. |
По физическому смыслу критерий согласия
Пирсона![]() -
это мера отклонений опытных данных от
теоретических.
-
это мера отклонений опытных данных от
теоретических.
Для того чтобы найти теоретическую
частость
![]() попадания вi–ый
интервал, необходимо сначала вычислить
отклонения от среднего значения и это
отклонение выразить в среднем
квадратическом отклонении для генеральной
совокупности, т.е.
попадания вi–ый
интервал, необходимо сначала вычислить
отклонения от среднего значения и это
отклонение выразить в среднем
квадратическом отклонении для генеральной
совокупности, т.е.![]() .
Например,
.
Например,![]() .
.
Результаты аналогичных расчетов сведем в таблицу
|
Размер, |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
-1,86 |
-1,22 |
-0,58 |
0,06 |
0,71 |
1,35 |
1,99 |
Затем, используя таблицу функции
распределения нормального закона
![]() найти соответствующие значения
найти соответствующие значения![]() .
Например, первому столбцу должно
соответствовать значение
.
Например, первому столбцу должно
соответствовать значение
f(39)=F(-1,86)–F(-1,22),
второму столбцу f(40)=F(-0,58)-F(-1,22) и т.д.
Примечание.При отсутствии таблицы
можно воспользоваться компьютером. Для
этого вExcelв какой-либо
столбец ввести значения![]() .Выделить
ячейку рядом с первым числом, вызвать
Статистические функции, НОРМСТРАСП и
в появившемся подменю указать первое
числох = –1,86. Ок. В ячейке появится
0,031, соответствующее
.Выделить
ячейку рядом с первым числом, вызвать
Статистические функции, НОРМСТРАСП и
в появившемся подменю указать первое
числох = –1,86. Ок. В ячейке появится
0,031, соответствующее
F(-1,86). Аналогично дляF(-1,22)= 0,111.
Вычитая, имеем
f(39)=F(-1,26)–F(-1,52)= 0,111-0,031=0,080.
Аналогичные и последующие расчеты заносим в таблицу
|
Размер, |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
-1,86 |
-1,22 |
-0,58 |
0,06 |
0,71 |
1,35 |
1,99 |
|
|
0,031 |
0,111 |
0,281 |
0,524 |
0,761 |
0,911 |
0,977 |
|
|
0.080 |
0.170 |
0.243 |
0.237 |
0.150 |
0.065 |
0.019 |
|
|
1 |
3 |
4 |
5 |
4 |
2 |
1 |
|
|
0,222 |
0,046 |
0,152 |
0,014 |
0,328 |
0,371 |
1,008 |
Суммируя последнюю строку, получим
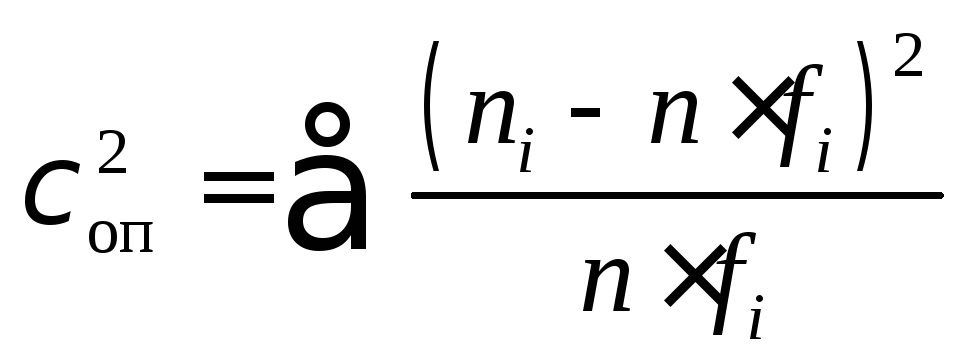 =2,142.
=2,142.
Необходимо сравнить опытное значение
с теоретическим значением. Теоретическое
значение![]() находят по специальным таблицам, Входом
в таблицу является гарантированная
вероятность и число степеней свободы.
Число степеней свободы находят по
формуле
находят по специальным таблицам, Входом
в таблицу является гарантированная
вероятность и число степеней свободы.
Число степеней свободы находят по
формуле![]() ,
гдеk– число разрядов
в таблице (в нашем случае число столбцовk=7);s–
число наложенных связей. Одна связь
присутствует всегда. Действительно,
если сумма вероятностей равна единице,
тоn-1 значений могут
быть любыми, а одна всегда равна
,
гдеk– число разрядов
в таблице (в нашем случае число столбцовk=7);s–
число наложенных связей. Одна связь
присутствует всегда. Действительно,
если сумма вероятностей равна единице,
тоn-1 значений могут
быть любыми, а одна всегда равна![]() .
Если потребуем равенства
.
Если потребуем равенства![]() ,
то это еще одна связь. Если потребуем
равенства дисперсий, то это еще одна
связь. Итого три. Следовательно, число
степеней свободы
,
то это еще одна связь. Если потребуем
равенства дисперсий, то это еще одна
связь. Итого три. Следовательно, число
степеней свободы![]() .
По таблице, для уровня значимости
.
По таблице, для уровня значимости![]() ,
при
,
при![]() ,
находим
,
находим![]() .
.
Вывод. Так как
![]() ,
то с вероятностью 90% можно утверждать,
что нет оснований для того, чтобы
отвергнуть гипотезу. Вероятность того,
что мы ошибаемся равна
,
то с вероятностью 90% можно утверждать,
что нет оснований для того, чтобы
отвергнуть гипотезу. Вероятность того,
что мы ошибаемся равна![]() .
.
Примечание. При отсутствии таблицы можно воспользоваться компьютером. Для этого вExcel вызвать Статистические функции, ХИ2ОБР и в появившемся подменю указать Вероятность 0,1, Степеней свободы 4. Ок. Прочитать ответ 7,77944.
Пример 1. 2.В казино поступила жалоба, что игральная кость с неравномерным выпадением очков. Необходимо проверить следуют ли экспериментальные данные закону равной вероятности. Для решения этой задачи проведен эксперимент, в котором произведено 600 бросаний.
Используем критерий χ2. Основная
гипотезаНо:![]() ,
конкурирующая гипотеза
,
конкурирующая гипотеза![]() .
Результаты эксперимента и промежуточные
расчеты отражены в таблице.
.
Результаты эксперимента и промежуточные
расчеты отражены в таблице.
|
Число
очков,
|
Их число в
эксперименте,
|
Теоретическое значение
|
|
Примечание |
|
1 |
101 |
100 |
0.01 |
|
|
2 |
86 |
100 |
1.96 |
|
|
3 |
107 |
100 |
0.49 |
|
|
4 |
94 |
100 |
0.36 |
|
|
5 |
97 |
100 |
0.09 |
|
|
6 |
115 |
100 |
2.25 |
|
|
Всего |
600 |
600 |
5,16 |
|
Суммируя, находим
![]()
Число степеней свободы:
![]() ;k=6 – число строк;s=3.
Следовательно, r
=6-3=3.
;k=6 – число строк;s=3.
Следовательно, r
=6-3=3.
![]() .
Так как
.
Так как![]() ,
то нет оснований для того, чтобы отвергнуть
гипотезу о равномерном выпадении очков.
Отклонения–следствие случайности.
Вероятность того, что мы ошибаемся
составляет 5%.
,
то нет оснований для того, чтобы отвергнуть
гипотезу о равномерном выпадении очков.
Отклонения–следствие случайности.
Вероятность того, что мы ошибаемся
составляет 5%.