
- •Негосударственное образовательное учреждение высшего профессионального образования санкт-петербургский филиал росноу
- •Статистика
- •Раздел 1. Общая статистика 8
- •Раздел 2. Математическая статистика 70
- •Раздел 3. 107
- •Список использованной литературы……………………………...206 введение
- •Раздел 1. Общая статистика
- •Предмет и метод статистики. Источники статистической информации
- •1.1. Предмет, метод и задачи статистики
- •1.2. Статистическая информация
- •1.3. Закономерность и случайность
- •1.4. Статистические показатели
- •1.5. Способы представления закономерности
- •2. Современная организация государственной статистики. Источники статистической информации
- •2.1. Организация государственной статистики
- •2. 2. Источники статистической информации
- •2.3. Статистическое наблюдение
- •3.Статистическая сводка, метод группировок
- •3.1. Статистическая сводка
- •3. 2. Метод группировок
- •3.3. Ряды распределения
- •Основные аналитические показатели рядов динамики
- •4. Статистические таблицы. Статистические показатели и система статистических показателей
- •4.1. Статистические таблицы
- •Прогнозы цен сырьевых товаров
- •4. 2. Статистические показатели и система статистических показателей
- •5. Средние величины и показатели вариации
- •5. 1. Средние величины
- •5. 2. Понятие о моде и медиане
- •5. 3. Вариация признаков и способы ее измерения
- •Раздел 2.Математическая статистика
- •1. Обработка данных выборки
- •1. 1. Предмет математической статистики
- •1.2. Понятие о генеральной совокупности и случайной выборке
- •1. 3. Оценка надежности статистических характеристик
- •1.3.1. Определение числовых характеристик при малой выборке
- •1.3.2. Оценка надежности значенийи. Ошибка выборки.
- •1.4. Определение вида закона распределения случайной величины.
- •2. Установление закономерности развития процесса и прогнозирование
- •3. Статистическое изучение взаимосвязей
- •3.1. Вероятностные зависимости
- •3.2.Определение степени тесноты линейной зависимости параметрическим методом
- •3.2.1 Парная корреляция и парная регрессия
- •3.2.2. Множественная корреляция и множественная регрессия
- •3. 3. Непараметрический метод оценки связи
- •3.4. Внутригрупповая и межгрупповая вариация признака
- •4. Использование стандартных программ Excelдля решения прикладных задач
- •1. Средние величины и показатели вариации.
- •2. Построение гистограмм
- •3. Однофакторная аналитическая группировка
- •4. Метод наименьших квадратов
- •Раздел 3.
- •1.2. Агрегатный индекс
- •1.3. Агрегатный индекс количественных изменений
- •1.4. Агрегатный индекс качественных изменений
- •1.5. Основные соотношения между агрегатными индексами
- •1. 6.Средние индексы
- •1. 4. Ряды агрегатных индексов
- •2. Статистика труда
- •2. 1. Показатели численности работников
- •2.2. Характеристики затрат труда
- •3. Статистика производительности и оплаты труда
- •3.1. Производительность труда. Основные показатели и методы расчета
- •Изучение динамики производительности труда
- •Понятие о статистическом парадоксе
- •3.2. Производительность общественного труда
- •3.3. Статистика оплаты труда
- •4. Статистика себестоимости продукции
- •4.1. Задачи статистики себестоимости
- •4. 2. Методы изучения себестоимости продукции
- •4.3. Основные показатели и способы их расчета
- •4. 4. Пути снижения себестоимости
- •5. Статистика прибыли и рентабельности
- •3. Изменение рентабельности производства
- •6. Статистика доходов общества
- •6. 1. Оценка уровня и качества жизни населения
- •6. 2. Показатели доходов населения
- •6. З. Показатели потребления населением материальных благ. Понятие о прожиточном минимуме
- •6. 4. Статистика цен
- •7. Статистика торговли, общественного питания и научно-технического прогресса
- •7. 1. Статистика торговли
- •7. 2. Статистика общественного питания
- •7. 3. Статистика научно-технического прогресса.
- •8.Статистика социально-общественной эффективности общественного производства
- •8. 1. Статистика основных фондов
- •8. 2. Общественный продукт и его структура
- •8.3. Статистика продукции промышленности
- •8.4. Оценка качества продукции
- •Основные термины и определения
- •Тесты статистика
- •Вопрос 22. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 23. При изучении динамики изменения себестоимости продукции рассчитаны: индекс постоянного состава1,1; индекс структурных изменений1,2. В этом случае индекс переменного состава равен
- •Вопрос 24. В минувшем году предприятием произведено и реализовано продукции
- •Вопрос 26. Располагаемые доходы населения – это:
- •Список использованной литературы
1.3.1. Определение числовых характеристик при малой выборке
Основными числовыми характеристиками выборки являются характеристика положения (среднее значение) и характеристика вариации признака (дисперсия).
Пример 1. 1.Предположим, решили создать мастерскую по пошиву мужской обуви. На какой размер обуви следует ориентироваться. Решили провести статистическое наблюдение: спросили у 20 случайных прохожих мужчин, какой размер обуви они носят. Оказалось
|
Размер,
|
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
|
Количество, |
1 |
3 |
4 |
5 |
4 |
2 |
1 |
20 |
Определить среднее значение измеряемой величины и дисперсию при малом числе измерений
Определяем средний размер обуви по формуле
![]() =
41,9.
=
41,9.
Находим дисперсию
![]() 2,29.
2,29.
Для прогнозирования необходимо оперировать параметрами генеральной совокупности, а не данными, полученными из случайной выборки. Каковы значения этих характеристик для генеральной совокупности ?
Теоретические положения.В соответствии с законом больших чисел, с увеличением числа измерений числовые характеристики, полученные в результате опыта, все более приближаются к числовым характеристикам генеральной совокупности.
Среднее значение для генеральной
совокупности обозначают
![]() и называют математическим ожиданием.
Вполне возможно, что в данном случае
и называют математическим ожиданием.
Вполне возможно, что в данном случае![]() .
Но если бы мы опросили других прохожих,
то получили бы другое значение
.
Но если бы мы опросили других прохожих,
то получили бы другое значение![]() ,
которое, вполне возможно, оказалось бы
,
которое, вполне возможно, оказалось бы![]() .
Следовательно,
.
Следовательно,![]() не
содержит систематической ошибки, т.е.
не
содержит систематической ошибки, т.е.![]() «является несмещенной оценкой». На
основании этого среднее значение
«является несмещенной оценкой». На
основании этого среднее значение![]() ,
полученное по результатам опыта, является
подходящей (приемлемой) характеристикой
случайных значений
,
полученное по результатам опыта, является
подходящей (приемлемой) характеристикой
случайных значений![]() .
.
В теории вероятностей доказано, что в
отличии от
![]() ,
дисперсия содержит систематическую
ошибку. Систематическую ошибку всегда
можно учесть с помощью коэффициента.
Введя поправочный коэффициент, формула
для определения дисперсии для малой
выборки принимает вид
,
дисперсия содержит систематическую
ошибку. Систематическую ошибку всегда
можно учесть с помощью коэффициента.
Введя поправочный коэффициент, формула
для определения дисперсии для малой
выборки принимает вид![]() .
.
Следовательно,
![]() и
и![]() .
.
Таким образом, в статистике принимают
|
Числовые характеристики | |
|
выборки |
генеральной совокупности |
|
|
|
|
|
|
1.3.2. Оценка надежности значенийи. Ошибка выборки.
Статистические характеристики всегда содержат ошибку. Предполагается, что ошибки определения статистических характеристик распределены по нормальному закону. Нормальный закон предполагается, что:
- ошибки не беспредельны;
- чем больше ошибка, тем меньше вероятность ее появления и наоборот;
- появление ошибки более 3
![]() –
практически невозможное событие.
–
практически невозможное событие.
Нормальный закон имеет место для
генеральной совокупности. Для выборки
ограниченного объема используют
распределение СТЬЮДЕНТА. Характерно,
что с увеличением числа опытов
распределение СТЬЮДЕНТА все более
приближается к нормальному закону. Так
как число измерений в нашем примере
всего n=20, то для оценки
точности![]() и
и![]() придется
использовать распределение СТЬЮДЕНТА.
придется
использовать распределение СТЬЮДЕНТА.
Для оценки точности статистических характеристик с использованием распределения СТЬЮДЕНТА составлены специальные таблицы.
Оценим точность значения
![]() =41,9,
рассчитанного по 20-ти измерениям:
=41,9,
рассчитанного по 20-ти измерениям:
1. Задаемся гарантированной вероятностью,
т.е. с какой вероятностью мы можем
утверждать, что полученный ответ верен.
Гарантированную вероятностью обозначают
буквой
![]() .
По физическому смыслу
.
По физическому смыслу![]() есть вероятность того, что найденное
значение
есть вероятность того, что найденное
значение![]() может
оказаться в области практически
невозможных событий. Вероятность такого
события должна быть небольшой. Пусть
может
оказаться в области практически
невозможных событий. Вероятность такого
события должна быть небольшой. Пусть![]() .
.
2.Рассчитываем среднее квадратическое отклонение для входа в таблицу по формуле
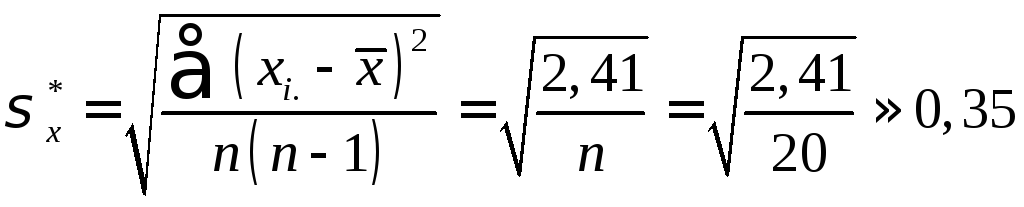 .
.
3. Используя специальную таблицу, находи
значение коэффициента СТЬЮДЕНТА, который
обозначают
![]() .
Входом в таблицу являются
.
Входом в таблицу являются![]() и число степеней свободы
и число степеней свободы![]() =19:
=19:
![]() .
.
Примечание.При отсутствии таблицы можно воспользоваться компьютером. Для этого вExcelвыделить любую ячейку, затем последовательно вызвать Статистические функции, СТЬЮДРАСПОБР и в появившемся подменю указать: Вероятность 0,1; Степени свободы 19, ОК. В выделенной ячейке появится число 1,729133 (значение коэффициента СТЬЮДЕНТА).
4. Рассчитывают величину доверительного
интервала
![]() .
.
Смысл полученного результата: вероятность того, что мы ошибаемся равна 0,1. С вероятностью 0,9 можно утверждать, что истинное значение mхне выходит за пределы доверительного интервала 41,9±0,6, т.е. находится в пределах 41,3 <mх< 42,5 или на рисунке
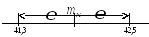
Аналогично рассчитывается доверительный интервал для дисперсии, но при этом используется другая таблица и несколько отличная методика.
Ошибка выборки. В теории вероятностей численное значение
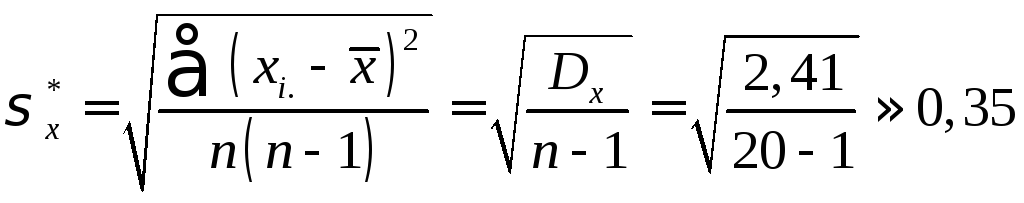 называют
среднее квадратическое отклонение, а
значение
называют
среднее квадратическое отклонение, а
значение
![]() –
доверительным интервалом.
–
доверительным интервалом.
В статистике введена другая терминология:
![]() –
средняя ошибка малой выборки;
–
средняя ошибка малой выборки;![]() –
предельная ошибка малой выборки.
–
предельная ошибка малой выборки.
