
- •Глава 1. Основные положения теории гиперкомплексных динамических сис тем 7
- •Глава 2. Целевые характеристики систем 30
- •Глава 3. Деятельность 83
- •Глава 4. Деятельностный анализ гиперкомплексных динамических систем 128
- •Глава 5. Особенности реализации и функционирования деятельностных си стем 162
- •Глава 1
- •1.1. Введение в теорию гдс
- •1.2. Основной закон гдс
- •1.3. Замкнутые и разомкнутые гдс
- •1.4. Соотношение гиперкомплексных неопределенностей
- •1.5. Относительность и принцип гомоцентризма
- •1.6. Концепция развития в теории гдс
- •1.8. Анализ взаимосвязи системных понятий
- •1.9. Разноаспектные характеристики систем
- •1.11. Ситуационный анализ и задача адекватности
- •1.12. Ограничения и область применения гдс-подхода
- •2.1. Особенности процесса введения новых понятий в инвариантном моделировании
- •2.2. Предпосылки процесса целеопределения систем
- •2.3. Общая характеристика процесса определения системной цели
- •2.4. Внутренняя цель гдс
- •2.S. Определение внешней цели
- •2.6. Пространство целей
- •2.7. Движение в пространстве целей
- •2.8. Пирамида целей в пространстве состояний
- •2.9. Определение массы пирамиды целей
- •2.10. Системная неопределенность и реализация целевой функции
- •2.11. Система ценностей в системе целей
- •2.12. Ограничения в применении целевых понятий и закономерностей
- •Глава 3 деятельность
- •3.2. Ортогональные компоненты деятельности
- •3.3. Деятельность в замкнутой гдс
- •3.4. Деятельностный анализ стационарного режима сложной гдс
- •3.6. Матричный учет результатов системной деятельности
- •3.8. Целеопределенная деятельность
- •3.9. Особенности деятельности как системного понятия
- •3.10. Общая характеристика составляющих системы деятельности
- •3.11. Функциональный аспект деятельностного анализа
- •3.12. Субъект и объект в системе деятельности
- •Глава 4
- •4.1. Введение в деятельностный анализ
- •4.2. Определение объекта деятельностного анализа в сложной системе
- •4.3. Оценка уровня системной организации
- •4.4. Определение нормативного базиса в задачах системного анализа
- •4.7. Анализ ротационной деятельности
- •3. Общие замечания.
- •4.8. Анализ оптимального процесса системной деятельности
- •4.9. Человек в системе деятельности
- •4.10. Особенности процессов целеполагания в системах человеческой деятельности
- •4.11. Контроль деятельности
- •5.1. Анализ управляемости доятельностной системы
- •5.3. Система деятельности с доминирующим центром
- •5.4. Гармонизация деятельности
- •5.10. Деятельностная интерпретация генезиса производных гдс
5.4. Гармонизация деятельности
Раскроем содержание процесса гармонизации деятельности путем перечислении следующих его свойств и особенностей,
1. При гармонизации обязателен учет всех компонентов деятельности по всем параметрам деятельностпого процесса. При этом, например, в сложном субъекте деятельности ни один из микросубъектов не игнорируется (как по составу микроцелей, так и по возможности их реализации в общей системе деятельности).
Сама деятельность всегда многомерна в своей реализации. Число щелевых траекторий при этом равно числу микроцелей, для реализации которых гарантируется пропорциональное ресурсообеспечение. Взаим ное исключение нелеп, так же как элементного состава, отсутствует.
Деятелыюстный процесс по направлениям отдельных микроце лей идет по оптимальному (с позиции ресурсных tarpai) пути ■-- в виде самореализации, конкретное видопроявление которой определяется без внешнего воздействия и лишь регламентируется габаритами допусти мой зоны деятельности (верхний и нижний пределы процесса самореали зации, допустимые орбиты u планетарной модели и т. д.).
Внутренние межэлементные взаимодействия в сложной системе деятельности идут с соответствии с основными закономерностями взаимодействия и развития сложных систем.
Устойчивость сложной системы обеспечивается за счет более •сильных внутренних взаимодействии между элементами нижнего уров ня по сравнению с межэлементным взаимодействием внутрисистемных макроэлементов. С ростом иерархии взаимодействие между элемен тами более высокого уровня падает сравнительно с взаимодействием на нижних уровнях.
Микродеятельностные процессы реализуются в состояниях, близких к замкнутым (по относительной оценке), что обеспечивает об щий деятельностный оптимум системы в целом.
Проанализируем особенности реализуемости сформулированных выше условий. Является очевидным, что при полной замкнутости сложной системы деятельности, рассматриваемой в целом, одновременный рост (реализация) всех деятелыюстных компонентов на всех уровнях невозможен. Это следует из соотношения гиперкомплексных неопределенностей, а также из ограничений, вызванных конечной величиной системообразующего ресурса. Такая особенность наиболее явно проявляется, когда анализируемая сложная система деятельности (близкая к изолированной) находится на завершающей ста тип своей деятельности и возможности ее дальнейшего развития полностью исчерпаны либо близки к нулю.
В условиях насыщения (исчерпания) деятелыюстного процесса возможны следующие варианты реализаций системной деятельности.
Разрыв замкнутости общей системы деятельности. При этом про исходит переход из стационарного в режим развития. Этот подход тре бует расширения запасов системообразующего ресурса, так как сопро вождается резким увеличением его потребления. Такой вариант можно назвать экстенсификацией деятельности с проявлением внешней экспансии.
Реорганизация деятельности без общего увеличения потребления системообразующего ресурса. Это путь взаимного качественного пре образования внутренних компонентов Например, такой вариант мо жет быть реализован средствами пуль-транспортпровки. При этом ре зультирующий уровень системного развншя никогда не превышает некоторого четко определенного предела, достижение которого яв ляется достаточным условием для начала процесса перехода всей систе мы либо ее компонентов в новое качественное образование.
В первом случае происходит удовлетворение гармоничности (сбалансированно-пропорционального развития) по амплитуде, во втором — по фазе (путем обеспечения цикличности в качественных преобразованиях).
Существование системы деятельности в виде идеального много мерного гнраюра. При у 1ом происходи i процесс камее iwиного преобра зования компонентов системы. Сбалансированность процесса приводит К уенжчпиому (по носпрпя I mo) eymeci iioiiainiio шдельпич компо нентов, так как такие преобразования (еаморл.чрушепня и саморазви тия) строго сбалансированы и находятся в динамически устойчивом равновесии.
Параллельный переход (одновременность) всех компонентов системы в повое, менее ресурсоемкое состояние (качесшо), чт обеспе чивает возможность дальнейшего экстенсивного развншя (кя общего увеличения расхода системообразующего ресурса. Этот переход может быть осуществлен при изменении имеющейся формы существования на более «тонкий» вариант се реализации. Например, аналогичные по сложности, уровню систематизации, адекватные по другим системным закономерностям системы деятельности могут быть реализованы из вещественной и половой субстанций. В данном примере полевой вариант может быть интерпретирован как более «топкий».
В силу невозможности одновременной реализации по всей совокупности системпых'аспектов (параметров, закономерностей) процесс гармонизации может проводиться, например, путем последовательной реализации во времени либо за счет избирательности и самоограничения числа гармонизируемых компонентов, а также па основе других корректировок, проводимых в соответствии с основными принципами и закономерностями системного развития.
На практике особенно существен учет и анализ подобных явлений в различных системах человеческой деятельности, субъектом п объектом в которых могут являться сами люди либо объекты, имеющие непосредственное отношение к жизни люден.
S.S. Кризис в системе деятельности
Кризис — это недоопределепно-переходпое состояние системы, отличающееся неустойчивостью и равновероятностью исхода альтернативных вариантов системной деятельности.
Под альтернативностью вариантов в процессах системного развития подразумевают, как правило, совокупность по крайней мере двух возможностей: продолжения дальнейшего развития н начала распада системы. По отношению к деятельности это может выражаться наличием двух потенциальных возможностей: полезной деятельности (прогнозируемой, желаемой, целеонределеппоп, upoi ресспвпой) и аптил.ен-телыюстн (непредвиденной, нежелательной, с аптицелями, регрессивной).
Кризисы в целом можно разделить на естественные, обусловленные совокупностью внутренних процессов развития системы, и искусственные, вызванные посторонним воздействием па процессы развития (на
состояние системы, деятельность и т. д.).
Рассмотрим примеры системных кризисов и некоторые причины, приводящие к их возникновению.
1.
Кризисы иерархического развития.
Деыльпые процессы иерархического
ciiciCMiioro
развития
и их зако-померпосш,
факгуемые в смысле теории
ГДС, изложены в 116], где кризисные
С0СЮЯ1ШЯ на графиках процессов СИС1СМ1ЮЙ
реализации для иерархиче ски
сложных систем обозначены как зоны
г. Простейший пример зоны г
представлен
на рис. 5.1, на котором отображен
двухуровневый (по иерархии) процесс
системной реализации с укрупненным
изображением области кризисного
развитии (зона г). Дадим кра гкое описание
генезиса кризисного явления в данном
варианте и отметим ряд его особенностей,
интерпретируя
их рис. 5.1. На рисунке приведен также
процесс развития произвольной
деятельности, где кривая Rx
отображает
деятельностный процесс
нижнего иерархического уровня. В сложной
системе деятельности может одновременно
пр.оислодшь конечное множество процессов
на определенном иерархическом уровне.
Общее число их в первом приближении
(при прочих благоприятных условиях)
определится запасами
системообразующего ресурса, который с
течением времени может
быть весь израсходован па микросистемы.
Просуществовав некоторое
время в условиях ресурсной недостаточности,
а также при наличии
определенной неполноты замкнутости,
микросистемы нижнего иерархического
уровня неизбежно будут либо распадаться
после определенного времени
стационарного состояния (распад
происходит по отрезку
АА'В
и
далее по штриховой кривой до нулевого
уровня), либо вступать
во взаимодействия между собой, образуя
следующий иерархический слой (кривая
R2).
Если
распад произойдет, то дальнейшим
вариантом
может бы гь только режим самоповтрспин,
возможно в ином качестве,
но на том же иерархическом уровне (кривая
R3).
Такое
развитие
процесса деятельности соответствует
принципу нуль-транспортировки
[15, 16] и может рассматриваться как один
из вариантов выхода системы
из кризисного состояния.
ски
сложных систем обозначены как зоны
г. Простейший пример зоны г
представлен
на рис. 5.1, на котором отображен
двухуровневый (по иерархии) процесс
системной реализации с укрупненным
изображением области кризисного
развитии (зона г). Дадим кра гкое описание
генезиса кризисного явления в данном
варианте и отметим ряд его особенностей,
интерпретируя
их рис. 5.1. На рисунке приведен также
процесс развития произвольной
деятельности, где кривая Rx
отображает
деятельностный процесс
нижнего иерархического уровня. В сложной
системе деятельности может одновременно
пр.оислодшь конечное множество процессов
на определенном иерархическом уровне.
Общее число их в первом приближении
(при прочих благоприятных условиях)
определится запасами
системообразующего ресурса, который с
течением времени может
быть весь израсходован па микросистемы.
Просуществовав некоторое
время в условиях ресурсной недостаточности,
а также при наличии
определенной неполноты замкнутости,
микросистемы нижнего иерархического
уровня неизбежно будут либо распадаться
после определенного времени
стационарного состояния (распад
происходит по отрезку
АА'В
и
далее по штриховой кривой до нулевого
уровня), либо вступать
во взаимодействия между собой, образуя
следующий иерархический слой (кривая
R2).
Если
распад произойдет, то дальнейшим
вариантом
может бы гь только режим самоповтрспин,
возможно в ином качестве,
но на том же иерархическом уровне (кривая
R3).
Такое
развитие
процесса деятельности соответствует
принципу нуль-транспортировки
[15, 16] и может рассматриваться как один
из вариантов выхода системы
из кризисного состояния.
Процесс образования следующего иерархического уровня, так же как и любой У?-процесс, находящийся в начальной фазе, всегда наиболее замедлен по скорости своего развития именно па начальном этапе. Такое замедление начального этапа переходного процесса в иерархическом развитии сопровождается в силу указанных выше причин образованием зоны неустойчивости, выделенной па рис. 5.1 окружностью. При этом назовем участок деятелыгастпою процесса, находящегося в окрестности отрезка ЛА', предкризисном областью; зону отрезка А'В — областью интенсивного развития кризиса; точку В— вершиной кризисного процесса; участок ВВ' — началом выхода из кризиса; точку С — окончанием кризисного процесса; заштрихованный участок,
находящийся между отрезками АА' и В'С — областью максимальной неопределенности кризисной зоны г\ точку А — теоретическим началом, а точку С - — теоретическим окончанием кризисного процесса.
В значительной мере указанные названия раскрывают суть и особенности различных аспектов кризисного процесса. Необходимо помнить, что зона неопределенное!п, рассматриваемая в целом, сосюитиз двух разнородных по качеству участков — верхнего участка допустимых значении /^-процесса для спсюм нижнего иерархическою уровня (интервал от 0,9/?! до I/?,) и участка (по нижнему порогу) допустимых значений /^-процесса для спетом второго иерархического уровня (кривая R.it иптерплл от |/\, до 0,1/ч'2). В пределах лих примыкающих друг к другу интервалов существуют не только качественные различия, обусловленные характером различных /^-процессов, но и количественные соотношения (масштабные, оценочные, и т. д.).
Данный вариант кризисного явления — ярко выраженный процесс с двумя альтернативными исходами, сопровождающимися двумя вероятностями реализации (распад и дальнейший рост).
Полное
вероятностное уравнение для сложной
системы, находящейся
в условии иерархического развития,
имеет вид (для каждой точки
графика на рис. 5.1)![]()
где
р1
—
вероятность пребывания в устойчивом
состоянии, например в
области стационарного развития; р2
—
вероятность системного распада;
р3
—
вероятность перехода в новое качество
(от систем нижнего иерархического
уровня — к системам следующего уровня
развития). Очевидна
и понята взаимосвязь указанных
вероятностей. При этом область
кризисной зоны характеризуется тем,
что в выражении (5.16) соотношения
между вероятностями примут
вид
примут
вид
С учетом (5.17) уравнение (5.16) можно в первом приближении переписать для кризисной зоны так:
Выражение
(5.18) дает![]() соотношение
между альтернативными вариантами.
При этом вероятность их осуществления
меняется с течением времени:
соотношение
между альтернативными вариантами.
При этом вероятность их осуществления
меняется с течением времени:![]()
По соотношениям (количественным) величии рг и ря, учитывая (5.19), можно определить характер протекания кризисного процесса и даже классифицировать кризисные участки.
При
выполнении условия (5.18) характерны
следующие зависимости между
вероятностями системных состояний и
соответствующими участками
зоны г:![]()

Следует отметить, что оценка вероятное гей вида (5.20) может происходить в данном случае по крайней мере с двух позиций (базисов). Одному базису может соответствовать любая система нижнего иерархического уровня, второму — верхнего. При эюм субъективная оценка вероятностей, следовательно, п степень определенности деятелт кого процесса для одного и того же момента времени будут различны. Например, участок ВБ' с позиций нижнего ба шел трактуется как явно соответствующий условию р2 ^ р3, ас позиции верхнего базиса вероятностная оценка будет рг ~ /;а или величина и взаимосвязь р2, рл оцс-
нипается определенмо.
Описанный кризис развития может быть предсказан теоретически путем системного прогнозирования или определен па основе эмпирических результатов наблюдении за реальном системой деятельности.
2. Кризисы вырождения деятельности. Нсли многомерная деятель ность реализуется, например, в виде системы с доминирующим цент ром, то при полном расходе системообразующего (деятелыюстиого) ресурса обязательно наступает кризисное состояние. Его альтерна тивные возможности для замкнутой ГДС - множество других реали заций с доминирующим центром (по числу нереализованных в первом случае составляющих). Kpiniicni.ii'i процесс по сноси форме поведения близок к процессу, описанному в п. 1 и отличается от него предысто рией (генезисом) большим качественным многое бразием альтернатив ных вариантов, усугубляющим степень неопределенности между ве роятностями исхода (сильная зависимость от внешних воздействий на систему деятельности), отсутствием возможности перехода на более высокий иерархический уровень (процесс развития возможен только в соответствии с принципом нуль-транспортировки).
Конкретный пример данного кризиса — диктатура (как форма деятельности), переворот (как кризисная зона), смена одной диктатуры другой (как результат выхода из кризиса). Это классический пример деятельностной системы с доминирующим центром.
В своем развитии подобные системы резко ограничены по уровню (минимальные возможности роста). Как следствие этого — деятельность в виде самоповторения (замкнутая окружность вместо спирали), с изменением «окраски» дея!елыюстп при тон же максимальной «амплитуде» достижений по всем альтернативным вариантам.
3. Кризисы замкнутой деятельности. Этот кризис по своим недо статкам может представлять сумму официальных моментов, приве денных в п. 1 и 2 кризисов, а именно: при иерархическом развитии жест ко замкнутой системы передаются по наследству при переходе с одного уровня иерархии па другой дефекты оболочки и тела системы [16], при чем с каждым уровнем дефект усугубляется, что неминуемо приводит к кризису, и если не будут принят специальные, внесистемные меры, такая система с Дефектом неминуемо распадется. Вероятность распада в подобной стуацнп пропорциональна числу иерархических уровней, времени пребывания в стационарном состоянии на каждом уровне (наи-
больший удельный вклад в вероятность распада), степени замкнутости, начальному количеству дефектов, числу дисгармонических и анизотропных явлений (микропроцессор связанных с неоднородное и.ю p.i t вития данной системы деятельности).
Конкретный пример подобной деятельности — вымирание замкнутых популяций; вырождение и деградация малочисленных семенеш, слоев, кланов при отсутствии внесистемных браков (смешанных семей) и т. д.
Рассмотренные примеры возникновения кризисов не единичны. Они приведены как иллюстрация того, что области неустойчивое!и - чго закономерные процессы в различных деятельностью системах. Знание закономерностей системного pa.inn i и я и опережающий .мыли t (и рот по зпронаппе п аи ищи наци я и системах деяю/и.носш) процтои функции пиромания могут помочь как предвидеть, так и и (бежать крншепых явлении за сче1 регулятивного воздействия на ход системных собыпш
5.6. Bz.-кризисная деятельность
1 кчюльзуя в качестве исходных данных примеры крп шеш t\ явлений, рассмотренные в параграфе 5.5, определим условия, при ко торых в ходе реализации системной деятельности можно было бы пред-отвратить волшкповение кризисов.
1. Устранение кризиса иерархического развития. Вариант бсекрп jiiuiui о pikinii 1 ни дли сложном трехуровневой сметены деятельное! и приведен па рис. 5.2, где буквами /1,, Л.,, Ля обозначены предельные уровни для трех /^-процессов (Rlt Rit Rs). Зоны кризисов zt и гг выделены окружностями, как и па рис. 5.1. Буквами /?2 и Ri обозначены потенциальные кризисные варианты иерархических переходов, которые предлагается устранить из общего процесса системного развития с целью избежания кризисов. Заштрихованными зонами выделены области перехода D, и D2 между иерархическими уровнями.
Суть
предлагаемого варианта видна
из рис. 5.2. Отметим ряд особенностей.
В отличие от педоопределен-ных
кризисных зон г области D
переопределены.
Это значит, что в одни и тот
же момент времени в пределах области
D
существует
независимо друг от
друга некоторое множество (минимум
— два, как эю видно из рис. 5.2) вариантов
деятелытостных процессов (переопределеиноегь),
которые не являются
альтернативно-взаимоисключающими
(как jto
есть
в зонах г)
и
имеют
одно усредненное направление (множество
нариапюи одной тенденции).
Аналитически эквивалентность
{оЛПОПЛПр.'ШЖЧНЮСТь) •1О11Д(ЧПип"| МОЖНО О11(4 III I I. ШИКОМ lipoll 111ОД11ЫХ --
п областях D все ироизиодпыо для любою n.i существующих а пей /^-процессов имеют один знак, а в зонах г знаки взаимно противоположные. Указанные явления в областях D можно назвать плюрализмом реализаций процессов системной деятельности.
Теоретически
бескризисный переходит RY
к
R.z
можегосущесшляться
на протяжении всего плоского участка
нижнего /^-процесса вплоть до
зоны г.
Особенностью
более позднего (по времени) начала
перехода является
то, что теряется деятельное! ный темп,
если переход (точка пересечения
нижнего и верхнего /^-процессов)
осуществляется слишком поздно.
Выражение «слишком поздно» может иметь
строгую математическую
интерпретацию — по абсолютной величине
(количественная оценка)
производных для кривых /?, и /<?2,
а ижже по разности этих величин.
Например, условием идеального (равномерно
иерархического) бескризисного
развития можно считать ситуацию, когда
в момент перехода![]()
В свою очередь неравномерность перехода, которую можно интерпретировать как неоднородность (аннзофопность) деятелыюстного процесса, можно оценить как .
![]()
В выражениях (5.21) и (5.22) величины типа —т~ —это производные
по времени соответствующего процесса системной реализации; А (/?„, Rn+i) — разность соответствующих производных для /^-процессов Ran Rn+\.
Используя изложенные выше методологические средства теории ГДС, можно дать более подробное описание (например, в символической форме) предлагаемого варианта бескризисного развития, а также сделать более глубокий системный анализ описываемого явления. Такой углубленный апллнз выходи т за пределы задач, решаемых и данной работе. Он предлагается в качестве упражнения тем читателям, которые захотят проверить на практике свой уровень понимания закономерностей теории ГДС. Здесь же отметим лишь некоторые особенности, важные при реализации предлагаемого подхода в многочисленных системах человеческой деятельности.
Выбор момента перехода, так же как и начало деятельностного процесса следующего иерархического уровня, в общем случае определяется целями реализуемой системы деятельности и условиями, в которых она функционирует. Серьезные ограничивающие факторы такие: запасы системообразующего ресурса, которых должно хватить на параллельную и многомерную одновременную деятельность в областях D; дея-тельностные возможности субьекта деятельности; внешние воздействия.
В сфере человеческой деятельности облас i и D можно интерпретировать как процессы демократизации деятельности. Действительно, рас-
ширение зоны денюлыюешых во 1можиос1сй приводиi к расширению возможных ii;ipu.in юн, чю важно для субьекта деятельное:и, осли им являемся человек И свою очередь расширение дея icjibiioci n сопровождаемся увеличением зоны дипуелнмого о|клоисиии по neon ip.iewiopiiu /^-процесса, причем допуск увеличивается по мерс перехода с нижнего уровня на высший. В системно-логическом смысле можно огмешгь, что такой способ реализации (при расширении допусков) приводи] к созданию устойчивой общей результирующей системы деиюлыюеш, гарантом чего являются именно указанный выше постепенный переход от «жестких» начальных конструкций (базовых, основных, скелсшых) нижнего уровня иерархии ко все более «мягким» системным образованиям высшего иерархического уровня.
2. Преодоление кризиса вырождения (на примере системы с доминирующим цепiром). Данный кризис можно предо! врапиь путем ухода от одномернои (доминирующей) деятельности к многомерной, реализуемость варианта котрои должна быгь близка к равновероятен и течение всего /^-процесса в сложной деятельностной системе. Очевидно, что масштабы О1дельиых многомерных реализаций бу/iyi в несколько раз (по числу многомерных вариантов) ниже масипаоов деятельности с доминирующим цен 1 ром Определяющие условия реалп ^смосш предлагаемого варианта избежания кризиса такие: сбалансированное распределение ресурса по всем одновременно реализуемым вариантам, гармонизация многомерной деятельности (но целям и траекториям реализации). Примером-аналогом для данного случая может быть переход от толстого, сплошного, монолитного оалмюго ipoca, поперечная трещппл п котром равносильна системно-деятелыюстНому кризису, к канату 1акого же сечения, по реализованному из мпожес1ва оiдельных, идущих в одном направлении тонких скальных нитей, что резко повышает прочность (кризисоусгойчиво^гь) каната. В системах человеческой деятельности близким примером может быть переход от индивидуальной деятельности одного человека к коллекгивпой хорошо организованной деятельности, в пределах которой нагрузка отдельного индивидуума существенно меньше (по общей оценке), чем нагрузка субъекта-единоличника. Живучесть такой многомерной системы выше, легко преодолеваются отдельные микрокризисы, например потеря отдельных мпкросубьек юп доя гельпосги и т. Д.
3. Преодоление кризисов замкнутости. Кардинальным средеibom в данной стуацин является разрушение системной замкнутости, проводимое па основе научно-аргумеп тированного upoi носшчеекого анализа сoipaGoiKoii возможных сшуацнн на миделях в ускоренном ц'мпе. Ликвидация замкнутости может идти как по любой системной ин-вариате, так и по набору инвариант одновременно.
В chciomcix человеческой деяюлыюсти выбор га >\т\ пы^чого компонента (системной иньирнапш) должен пронсхо'ипь па основе анализа внутренних закономерностей реконструируемой системы (путем тщательного учета человеческого факшра во всех дея1ельностных составляющих системы) и (О фовождагься постоянной ориентировкой проводимых преобразовании па поставленные перед человеком цели реконструкции.
Процесс системного размыкания должен быть управляем и контролируем для того, чтобы не привел размыкаемую систему в состояние самораспада. Особенно важен таком контроль, если исходная система находится в близкой к предельном падин развития, когда свободного системообразующего ресурса практически пег. К наиболее серьезным необратимым последствиям может привести реализация неконтролируемых структурных и эмергентных размыканий.
В заключение отмстим, что в глобальном смысле абсолютно полная ликвидация кризисных явлении (как идеальный вариант) невозможна. Реализуемы только компромиссные варианты, способные в значительной мере с помощью определенного набора системных параметров смягчить переходный процесс между различными системными состояниями. Выбор оптимального числа сглаживающих системных функций (составляющих, системных инвариант) приводится в процессе целепола-гания. Он может быть спрогнозирован но предполагаемому результату и реализован на основе конкретной метлики, ба шрующепся па закономерностях теории ГДС.
5.7. Предельные оценки в системе деятелькости
Рассмотрим общие положения, отображающие один из вариантов оценки предельных деятельное i пых возможностей системы. Для того чтобы суть подхода "была максимально ясной, приведем пример анализа изолированной (от внешнего воздействия) ГДС, находящейся в режиме аптпомпой деятельноеm (процесс самореализации в условиях конкретно заданного системообразующего ресурса).
Пусть в качестве исходных данных имеем системообразующий ресурс W, из которого необходимо в процессе дея1елыюетм носiроить систему S. TpeCyeini оценить копетрукпшные пределы многообразия возможных вариантов (реализаций) системы S.
Краткие замечания к исходным данным, формулировке задачи и подходам к ее решению следующие.
Из одного и того же ресурса можно построить некоторое мно жество систем \Sn |, которое назовем множеством возможных конкрет ных реализаций спемемы S па основе исходного ресурса W.
Наложение конкретных ограничений па какие-либо системные параметры в конкретно реализуемых системах позволяет определить однозначно размеры множества JS'"1). Иными словами, заданием на чальных ограничений можно варьирован, число п (возможное число конкретных реализации спск'мы S).
Опенка пределов системной деяк'лыюстп может проводиться только при наличии оценочных критериев и указании системных па раметров, подлежащих опенке.
В каждом копкрет ном случае (по мс ре необходимости) можно ого варивать дополнительные частные сисгемпые условия, в соответствии с которыми должен проходить оценочный процесс. Например, ого варивается базис, с позиций коюрого проводится оценка; задается ис ходная система ценностей, в пределах по горой проведенная оценка яв-

ляется достоверной и можег бы п> Minepnpei пропана суш.с к к>м дея uvn>-пости и т. д.
С учетом сделанных замечаний приступим к решению задачи. В качестве копкрешых исходных условий будем рассматрипагь ресурс W, преобразовав его в простейшую системную разновидность SK) с минимальным уровнем систематизации. Получим
![]()
- Раскроем содержание последовательности (5.23). Исходный ресурс W рассматриваем как системообразующую среду So для системы S; Систему S создаем па основе выражения (1.1), определяющего ГДС в общем виде, учитывая при этом общее требование минимальности уровня систематизации. Минимум находим, подставляя в (1.1) значения i = 1, / == 1. В результате получим ГДС с единственной системной инвариантой (гиперкомплексностыо), реализуемой в одном качестве: (SJ1. Полученную таким образом ГДС будем рассматривать как простейшую системную разновидность и обозначим ее S<0>. Конкретная система S<0) может теперь интерпретироваться (рассматриваться) как исходный (начальный) конструктивный базис для производимых из нее новых, более сложных вариантов системы S. Рассмотрим конкретные примеры таких вариантов.
Оценим пределы конструктивного системного многообразия путем расчета предельных размеров (габаритов) для ряда простейших реализаций системы S из ее исходной (начальной) конкретной разновидности S(U). Для этого проанализируем ряд системных образований, изображенных па рис. 5.3, где окружностями условно обозначены элеметы, порядковый помер которых стоит рядом с окружиопыо. Существующие взаимодействия элементов и соответствующие им расстояния обозначены стрелками. При этом рис. 5.3, а отображает простейшую линейную ГДС без взаимодействий, рис. 5.3, б— цепочку из исходных элементов (линейная ГДС с взаимодействием), рис. 5.3, в — линейное замкнутое, однородное системное образование (линейный цнркулятор).
Остальные
буквенные обозначения будут разъясняться
по мере необходимости
п ходе анализа данных примером.
1. Линейная ГДС низшего иерархического уровня, без взаимодейст вий элементов (рис. 5.3, а). Исходная система S'0' — это несвязанный набор (совокупность) простейших элементов, число которых конечно и может быть однозначно определено (при конкретизации качествен ной разновидности ресурса и указания ресурсных расходов па одна элемент). Обозначим это исходное число п. Заданные п исходных эле ментов могут быть размещены в пространстве, например, в виде одно мерной линейной последовательности из плотно приставленных друг к другу элементов. Длина LL такого системного образования
В
(5.24) элементы рассматриваются![]() в
виде сферы радиусомг
(диаметр
d).
В
общем случае идеальный элемент ГДС —
это многомерный сфероид.
В частности, могут быть регламентированы
параметры тела и оболочки
исходного элемента (как частные исходные
условия). Здесь же для
простоты рассматриваем элементы в виде
одинаковых сфер. Длина Lx
в
(5.24) может интерпретироваться наряду с
диаметром d
как
габариты простейшей плохо
структурированной, без взаимодействий,
линейной
системы, собранной из S'01.
в
виде сферы радиусомг
(диаметр
d).
В
общем случае идеальный элемент ГДС —
это многомерный сфероид.
В частности, могут быть регламентированы
параметры тела и оболочки
исходного элемента (как частные исходные
условия). Здесь же для
простоты рассматриваем элементы в виде
одинаковых сфер. Длина Lx
в
(5.24) может интерпретироваться наряду с
диаметром d
как
габариты простейшей плохо
структурированной, без взаимодействий,
линейной
системы, собранной из S'01.
2. Линейная
ГДС со взаимодействием (рис. 5.3, б).
Более
сложное
образование
— линейная цепочка из последовательно
i
з
шмодействую-
щих
п
элементов.
При этом у(шкнн-1>
— взаимодействие элемента т
с
элементом (т -\-
1).
В первом приближении длину L2
такой
цепочки
можно
оценить,![]() пренебрегая
размерами элементов, по соотношению
пренебрегая
размерами элементов, по соотношению
где
R<mym+\)
—
системное расстояние между элементами
т
и
(т + 1), в
первом приближении определяемое по
соотношению (1.31)
при выполнении
условия (1.33). Дательно системное
определение понятия «расстояние»
и его интерпретация изложены в 1151.
В данном примере используем
простейшую разновидность ГДС-попятия
— «расстояние» Rnm,
определяемое
так:![]()
где Ynm взаимодействие элементов п \\ т в направлении от п к т.
Выражение (5.25) упростится, если цепочка взаимодействующих элементов однородна и все расстояния одинаковы:
![]()
С
учетом (5.20) можно пореипсап.![]() (~>.25)
в виде
(~>.25)
в виде
где (п — 1) общее число одинаковых расстояний, равное числу взаимодействий в простейшей системе.
Следует отметить, что в наиболее общем случае расстояние может оцениваться в относительных ед/ницах (снятие качества за счет операции нормирования).
3. ГДС в виде линейного циркулятора (рис. 5.3, о). В качестве предельных величин в данном примере можно принять длину стороны ^<ш)(ш-|-и правильного miioi оушлышка, составленною п.* шаимо-действующих (последовательно) элементов, замкнутых в едином цикле, и радиус Ra.m окружности, в которую вписано данное системное образование. Для простоты расчетов считаем линейный циркуля тор однородным (все взаимодействия одинаковы, окружность без деформаций). Расчеты ведем но соотношениям
где
/?<т)(ш-н) —
длина стороны многоугольника, образованного
элементами
циркулятора; а — центральный угол
многоугольника; л -число
сторон многоугольника; R{)m—
радиус многоугольника (расстояние
между базисом, обозначенным как нулевой
элемент, и произвольным
элементом т).
—
длина стороны многоугольника, образованного
элементами
циркулятора; а — центральный угол
многоугольника; л -число
сторон многоугольника; R{)m—
радиус многоугольника (расстояние
между базисом, обозначенным как нулевой
элемент, и произвольным
элементом т).
Сделаем следующие замечания к рассмотренным примерам.
Рассчитанные габариты могут быть уточнены, например, путем учета наряду с межэлементными расстояниями размеров самих эле ментов, анизотропных явлений, деформаций и т. д.
Расстояние удобно оценивать (при расчете) в относительных еди ницах. Для этого необходимо провести нормировку (по качеству и ко личеству) используемых величин Af<m)(m+o- Снятие качества может проводиться путем деления всех используемых при расчете значений AVuxm+i1' lia максимальное из них (шах (W(m)(m+i)}) либо на специаль но введенное единичное расстояние. Для перехода от обезличенного расчета к качественному анализу используемые относительные величи ны R(m)(m+\) перенормировываются и приобретают конкретную раз мерность.
В качестве объекта для предельных оценок могут быть использо ваны другие (геометрические, функциональные и т. д.) параметры, а также исследованы более сложные системные образовани я, вид которых определяется условиями конкретно решаемых задач.
Оценку системно-деятельностных пределов можно проводить не только путем расчета рассмотренных выше габаритных размеров, по и например, па основе определения граничных возможностей процессов системного развития. В частности, можно оценить предельно достижимые значения уровня систематизации для всего набора возможных реализаций, если в качестве исходного системообразующего материала рассматривать конкретную систему S<0>, которую можно интерпретировать как совокупность простейших одноэлементных систем.
Проведем такую оценку и укажем граничные уровни системной сложности, которых можно достичь (реализовать), используя системное множество S<0), состоящее из п одноэлементных систем.
Конкретизируя оцениваемые параметры формулируем пашу задачу в виде вопроса: каково максимальное число иерархических уровней

может быть реализовано на основе имеющихся исходных данных? Оценку будем проводить по системной инварианте — гиперкомплексности. Это тем более удобно, чш исходные данные сами по себе являются именно этой системной инвариантом (гипсркомплексностыо) и имеют однозначно определенную исходную оценку (число элементов (п) — как количественная оценка сложности по гиперкомплексности).
Рассмотрим последовательно ялапы решения, использовав для этого рис. 5.4.
Очевидно, чго наибольшее числи иерархических уровней может быть тогда, когда каждый ил реализуемых уровней максимально прост. При этом содержательный аспект «максимальной простоты» является понятием относительным и зависит от условий и ограничений, имею щихся в исходных данных.
В общем случае, при отсутствии специальных оговорок, наиболее простой из допустимо возможных является система из двух элементов. Это следует из того, что одноэлементная система (или система, состоя-
щая из изолированных друг от друга одинаковых элемептв) не- может сама по себе рассматриваться ни при каких условиях как снуема с иерархическими уровнями (перлрмпшооь по плрамефу «пшеркоми-лексноегь»). Именно такой системой без иерархии можно ечпипь исходно 1,'1Д,1|Инк' сиг Н'мпос множгс I in) о . Копкре I iiiiiM примером i.iko
го системного множества можно считать нижний иерархический слой 6" \ состоящий из восьми элементов, представленных па рис. 5.4, а. Обозначим чисто элементов в S(0) как п0 -- 8.
3. Ьсли 'i,'i,laiio пп эчемеигов, то п.ч них можно сочдап. конечное чис ло nL минимально простых (днухэлсмешпыл) ciicicm с иерархией, обь- единепных в системное множество S(1), которое оюбражепо во втором, начиная снизу, слое па рис. 5.4, а. При -ном
так как
в и,пнем примере![]() /(„
S
'2/п
-
//t
1,
осьпка пек ! >jm
нечетном
/;„ неиспользованным остаемся (для
предельного случая) один
элемеш нижнею уровня.
/(„
S
'2/п
-
//t
1,
осьпка пек ! >jm
нечетном
/;„ неиспользованным остаемся (для
предельного случая) один
элемеш нижнею уровня.
4. Рассуждая аналогично, получаем для нашего примера трети иерархический слой — системное множеспю S[2>, содержащее два сложных одинаковых компонента, из которых мо/<по построить четвер тый уровень (высший) — множество S(3), гостящее пл'очпого э.чемсчиа максимально возможной сложности (по числу иерархических уровней).
При этом для каждого рассматриваемого иерархического уровня, отображаемого множеством S'"', исходной системообразующей средой является системное множество S(/l—1>, относящееся к предыдущему слою (иерархическому уровню).
Для нашего конкретного примера получили искомый ответ: из ис-
ходпой системы S(0) можно носiроить систему с четырьмя иерархическими уровнями (если за элементы первого уровня иерархии принять исходно заданные элементы системы S(0)).
В символической форме найденные пределы системной сложности (по гнперкомплекспости) для системы 5 также могут быть записаны в виде условных габаритов — как произведение длины / (максимальное число элементов, равное исходному, заданному п„ == /) на высоту h (равна числу уровней иерархии) системной пирамиды, изображенной на рис. 5.4, «, аналогично тому, как это сделано в гл. 2 и 3. Такую оценку можно записать в виде
![]()
где Г (S) -- условное обозначение габарппкш оценки по системной пирамиде. Для нашего конкретного примера (рис. 5.4) Г (5) = 8 х 4.
5. В упрощенной форме, где указаны только последовательность операций и требуемые иерархические уровни (в виде горизонтальных линий) с числом элементов па них (по количеству точек па каждом уровне), рассмотренный конкретный пример представлен в виде схемы реализации на рис. 5.4, б. Процедура построения и конечный вид схе-
мы реализаций апалошчны процедуре дихотомического расчленения сложного объекта с последующим отображением лого процесса на основе его структурного графа. Там же, па рис. 5.4, б, с целью преемственности выделены общие контуры системной пирамиды.
Проведя обобщенным аналнл (по англогип с рассмотренным примером), представим в символической (Ьопме соотношение, позволяющее дать оценку предельных во шп.ынк ieu iijiuiirci .i шу.ф.чичеекот \ n.t-вития системы i' из исходно ладнппы.х // ш-мемти. Опуская детальные выкладки, выделяем некоторые момешы такого обобщенного анализа.
1. В первом приближении зависимость между п (число исходно за данных элементов) и N (порядок высшего реализуемого иерархическо го уровня) можно записать в виде соотношения
где
б (п)
—
остаток исходных![]() элементов,
не входящий в состав оптимально
организованной из 2N
элемеиюв
(по двоичному принципу) наиболее
сложной иерархической струюуры.
элементов,
не входящий в состав оптимально
организованной из 2N
элемеиюв
(по двоичному принципу) наиболее
сложной иерархической струюуры.
В свою очередь ил ft (//) оскишыхея мемснюг» также могут быть организованы аналогично конструируемые двоичные структуры, хотя и обязательно менее сложные по иерархии, чем iV-уровпевое образова ние. Отсюда следует, что и остаток сям по себе может быть проанализи рован и символически описан собсп;енным соотношением, аналогич ным (5.32).
В развернутом виде остаток и наиболее сложная компонента имеете с п исходно заданных элементе могут быть записаны в виде соотношения

где N — порядок иерархического уровня (см. рис. 5.4); п — число исходных элементов нулевого уровня; :г — целочисленный коэффициент, определяющий наличие (к, -= 1) или отсутствие (/гг — 0) соответствующей составляющей в сумме (5.33).
4. В
соответствии с (5.33) синтезированную по
двоичному принципу
систему
S
в
ее предельно сложном варианте развития
можно отобразить
в
виде числового ряда, состоящего из нулей
и единиц. Число членов
ряда
будет равно (N
+
1), а каждый член (по позиции и значению)
бу
дет
идентичен коэффициенту![]() /<■,:
/<■,:
Для нашего конкретного примера (рис. 5.4), в котором п Я, согласно (5.34) получим:
![]()
Выражение (5.35), соотнося его с (5.33) и учитывая изложенное выше, можно интерпретировать так: система 5 представляет собой четырехуровневое образование (если исходный уровень считать первым),

о чем говорит первая единица. При этом других образований (без оста; ка) нет (о чем говорит присутствие нулей).
Выражение (5.34) п его конкретная форма (5.35) могут быть iirun,iiib' двоичным генетическим кодом предельного развития.
Двоичную систему назовем опншалыюй, если для нес соблюден nv условие
При
соблюдении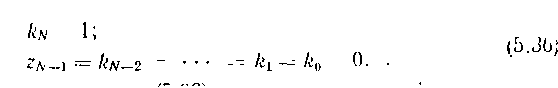 условия(o.iibj
система
условно-графически може! быть
представлена в виде правильной пирамиды.
условия(o.iibj
система
условно-графически може! быть
представлена в виде правильной пирамиды.
При
несоблюдении условия (5.36) конечный
продукт системной деятельности
может быть представлен набором правильных
пирамид раз ной
высоты. Число таких пирамид равно
количеству единиц в генетическом
коде, а высота каждой пирамиды определяется
позицией соответствующей
единицы. Сказанное проиллюстрируем
рис. 5.5, где отображены
схемы реализаций для двух различных
исходных ентуа ций
при таких![]() условиях:
условиях:
Как видно из данного примера, система S., (рис 5.5,6) является с и тимальной, а рис. 5.5, а отображает множество разноуровневых систем (для реализации оптимального варианта не хватило нсего лишь одно1с элемента!) — от одноэлементной пирамиды с нулевым иерархическиv утовпем до сложного образования с четырьмя уровнями (включая нуле юй уровень в общее число уровней). Отметим, что порядок (ранг) урошш и общее число уровней ра ишчаюк-я пп слшшпу, как ото гидт из pnec'Moiрепных примеров.
Проведенным анализ предельных возможностей (оценка по гипер комплексности) процесса системного развития не является единственно возможным, хотя и может быть рекомендован в качесте базового варианта. Аналогичным образом можно давать оценку по другим систем иым .инвариантам. В частности, учитывая взаимообусловленный ха-
рактер связи основных системных инвариант, можно либо приводить все другие оценки к их пшеркомплексному эквиваленту, либо указывать соотношение (плпрнме]), функциональное) между используемой системной инвариаптой п гпиеркомплскепсстыо.
Выбор двоичных систем в качеспзе базового примера обусловлен их большой распространенноеi ыо и значимое! ыо во многих теоретических и практических исследованиях, а также явным соответствием их свойств условиям ои'пшалыюсш, трак1}емым с нилщий теории ГДС в различных ситуациях.
5.8. Условие реализуемости системной деятельности
PaccMinpei пые в преды.!} щем параграфе подходы к опре делению предельных возможности рлоыпин систем деятельности могут служить основой для формулировки одного из общих критериев реализуемости системной ДСЯ1СЛЫЮС1П.
Действительно, найденные предельные возможности развития системы могут в сво.о очередь расами фь^иься как вариант максимально сложного продукта (результата дся 1СЛ]Л!осги), реализуемого исследуемой системной деятельности. Опеппгля ыкоп млкепмлльпып результат по каким-то обобщенным, пригодным для широкого класса систем параметрам, можно сформулировать ксикремные критерии системной реализуемости и использовать их па начальной стадии исследования -определенного класса деятельности их систем Целью начального исследования может быть выяснение такого важнейшего вопроса в ходе деятельностного анализа: возможно ли в принципе создание требуемого продукта из имеющихся исходных данных? При этом под требуемым продуктом можно понимать либо отдельную составляющую (результат) деятельностного процесса, в ходе которого создается этот продукт, либо всю систему деятельности в целом, которую на ее предельной ступени развития можно рассматривать также как вариант желаемого продукта деятельности. В качестве конкретных примеров отдельных составляющих (результатов) деятельностного процесса можно рассматривать отдельные пирамиды, приведенные па рис. 5.5, а. Полным (предельным, максимальным) результатом можно назвать либо всю совокупность пирамид (рис. 5.5, а), либо пирамиду (5.5, б).
Так как приведенные примеры конечных результаюв системной деятельности получены из определенных конкретно заданных исходных данных и являются иллюстрацией предельных возможностей системного развития, то па их основе молено решить и обратную задачу: по предельно возможным результатам сформулировать критерий, позволяющий априори, до реализации требуемой системной деятельности, оценить возможность такой реализации.
Опустив детальное изложение решения такой обратной задачи, приведем конечный результат, отмешв при этом ряд особенностей.
В данном случае конечным результатом будет формулировка искомого условия реализуемости системной деятельности, которое сформу-.лируем в виде следующего утверждения; системная оценка требуемого
продукта системной деятельности не может прсиышлп> тон же оценки, полученной по уровню предельного развития исходной гиен мы дея ц'ль-телыюст.
Приведем примечания к определению.
1. Наиболее часто оценочные варианты отображают в колпчех ты п- ной или качественной форме меру системною (в теории ГДС) разнооб разия в каждом конкретном случае проведения оценочных работ. В тео рии ГДС шюдп'к я понятие информации как меры I ДС-ра шо< dp л шя [151, которое может определяться как по отдельным системным иппа- рпащам (илрлмефлы, хлрак и'рнстиклм), так и но п\ югок} шкк 11: Например, рассмотренные предельные опенки норармиткот рлшп- тня (см. рис. 5.5) позволяют определит ь (гиепн и») стс пень рллпе cQ.a.'uiH по системной инварианте •— иерархичность. С учетом определения по нятия информации (в сг/ь.сле теории ГДС) и предлагаемых подходов к определению оценок, мгжио пригедеппсе i ып суп ерждепне в его част ном вариаые реализации рассматривай кал и.фор:.* иным ып KpiM- рнй роалп !\ем(;етп системной деятельности.
2. Пргскп ческая реализация с^ермульгетаппого уелсьнм ij4(>ui обязательною указания icx системных иш аригип, для кок рых опре делялась ia пли иная системная мера в каждом кош.рем ном сл}ч.к\ Промзг.о.'н мый перенос (цепочных речу.'м.тл ion с о nioi'i i- ;i чс> т i eimnii разновидноеiи системною параметра (ншарнанш) га другие) U\t \ка- заппя взаимосвязи между этими параметрами являемся ошибкой. На пример, более высокая степень разнообразия в конечном (предельном) продукте системной деятельности, соотгетствуютая конкретно задан ному качеству, является необходимым, по недостаточным условием для реализуемости в границах данной системы требуемого продукта друго го качеава даже при его зпачптел! но более низкой оценке по избран ному параметру.
3. Предложенное условие можно рассматривать кгк метатеоретн- ческнй, системный аналог известного закона необход! юго разнообра зия, сформулированного У. Р. Эшби [33]. Предлагаемый в теории ГДС вариант являемся более общим, так как можем бьпь реализован не толь ко па уровне информационного подхода, но и в виде набора рлзнокп- чествепных ГДС-оцепок, например, на основе определения «крнтиче-
t ской массы» как минимально требуемого системообразующего ресурса, необходимого для реализации конкретного продукта (или системы в целом) системной деятельности. Очевидно, что конкретизация «критической массы», например, информационными запасами есть частный случаи из широкого множества возможных ГДС-оцепок.
Переход от ГДС-условия системной реализуемости к его конкретной разпог.иднести, например, в виде информационного критерия, можно также осуществить, используя уже известные классические подходы к определению понятия игформлцш, и (е опенок i К), 32, 331, учшьп'ая при этм выражении (5.3.3) п (5.34). 11роиллюсфируе'м один из карп.ш-тов такой возможней: in, 1!ыделии при эюм еле 'укнцие моменты.
1. Величина п и (5.33)- исходная, которую и контексте пашей задачи можно рассматривать как ресурсный эквивалент исследуемой системы деятельности. В указанном смысле п можно считать продуктом,
полученным на основе ресурса W, что можно отобразить, например, в виде зависимости
Соотношение
(5.37) можно![]() получить
путем чисто абстрактно-логического
рассуждения: число /; всегда mojkci
бьпь
представлено как логарифм,
например двоичный, от числа W,
такого,
чтобы выполнялось соотношение
получить
путем чисто абстрактно-логического
рассуждения: число /; всегда mojkci
бьпь
представлено как логарифм,
например двоичный, от числа W,
такого,
чтобы выполнялось соотношение![]()
2. Рассуждая подобным образом, можно противопоставить каждому слагаемому в правой части (5.33) также свои логарифм. Например, для первого слагаемого запишем следующее соси ношение:

Учитывая![]() (5.37)
— (5.39), перепишем (5.33) в виде
(5.37)
— (5.39), перепишем (5.33) в виде
В традиционном, классическом смысле слагаемые в (5.40) можно интерпретировать как информационные оценки 1ц, шюдя соответствующие обозначении
С учетом
(5.41) выражения![]() (5.33)
и (5.40) перепишем в виде
(5.33)
и (5.40) перепишем в виде
![]()
В простейшем случае, учитывая, чю к, можег принимать значение 1 или 0 (иными словами, включать или не включать в состав суммы соответствующую информационную оценку) вмесю (5.42) для произвольной системы деятельности можно записать
![]()
Выражение (5.43) тождественно по своему содержанию закону сохранения информации в замкнутых ГДС 115, 101.
С учетом изложенного можно информационный критерий системной реализуемости записать в виде следующею соошошения:
![]()
где / (S) — информационная оценка требуемого продукта системной деятельности; / (So) — предельная информационная оценка исходной системы деятельности, средствами ко юрой предполагается получить требуемый продукт.
Проведенная конкретизации условия реализуемости системной деятельности не единственно возможная, а лишь иллюстративная. Используя другие системные оценки и закономерности, можно получить
требуемые
условиями конкретной деятельности
соотношения, обладающие
критериальным харак1ером. Например,
обобщая изложенное, а также
учитывая соотношение гпперкомплексных
неопределенностей, можно получить для
замкнутых систем деяк'лыюеш следующее
мета-теоретическое
кри i
ер
п алы![]() юсcooi
ношение.
юсcooi
ношение.
где АКОл — ншервал колпчес!штишп оценки спсюмного разнообразия; А,(,ч — интервал оценки по кпчосшу.
Выражение
(Ь.45) можно па.ibai
ь
законом сохранения и преобразования
системного разнообразия и учитывать
его в ходе функционирования
деятельноегных систем при определении
их граничных оценок. При эюм![]()
где t— время, за которое изменение компонент происходит противоположно и носит взаимообусловленный характер.
Наполнение сомножителей в (5.45) и (5.46) копкрешым смыслом может быть проведено в ходе решения частных задач Например, при проведении информационных оценок величины в (5.45) приобретают смысл КОЛПЧОС1ВСПП010 и качесчвеппого информационных iniiepi алой. Для случая определения условия реализуемое!и либо нахождении граничных оценок знак равенства в (5.45) должен бьпь вменен па з:.ак «больше» пли «меньше» аналогично тому, к.ж при no'i\ чппш eooinoiiio пин (5.4 1).
Одним из важнейших следе шин из (Г> '!.')) при реализации па нракш-ке систем деятельности можно считать еле тощее: для реализации конкретно заданной спечемы степень разтоираапя в исходных данных (например, по оценке системообразующего ресурса) не должна быть меньше определенного порогового значения — критической величины системного ['..ьнообра'Л'н
Данный вывод хорошо иллюстрируется рис. 5.5, когда расхождение исходных данных всего лишь на единицу (разнообразие по гипер-комплекепостн) делае! нереализуемой задачу построения сложного объекта (рис. 5 5,6), если рассматривать этот объект как требуемый результа! процесса функционирования копкрепюн епечемы деятельности.
Соотношения (5.44) и (5.45), так же как и сформулированные критерии реализуемости системной деятельности (в общей и частной формах), могут применяться не юлько для общесистемной4 анализа деятельнесг-иых процессов, по и для оценок сьойст и ovnC iinocieu фупкцпопаль пых составляющих произвольной СНС1СМЫ деи1елыюсп1, uikiix, как субьект, объек!, сродежа и резулыаты до я юлыюстн. Например, апа-лотчпо изложенному выше можно оцешиь н|)Н1однос1Ь копкрепюго субъекта деятсльпеечи (допустим, по психофизическим, интеллектуальным, ннформацпот ым и другим характорнечнклм к г'ьню.шоппю коп крешых pa6oi в пределах заданной спермы деянмыюсы.
При пеполь touaiiiin расемофеппых условии и кршерпси следуем помни i ь, чю они являю[ся необходимыми, по не всем да достаючпы-
ми условиями реализуемости. Оценка достатчностн должна проводиться дополнительно с учсчом копкрешо .ыдлнпыч исходных л.'ншых и ограничений, накладываемых на исследуемую спаему деятельности.
5.9. Деятельность и уровень системной организации
Системная деятельность, начатая с какого-то определенного уровня и стремящаяся в своем развитии к достижению предельных значений, может обладать различными потенциальными возможностями по реализации продуктов деятельности, что записи г как от исходных данных, так и от способа системной организации, а также or той фазы системного развития, в которой рассматривается эта деятельность.
Оценим нотепцналыю-деяюлыкк.iиыс возможиосш снечемш и зависимости от уровня сесплемпоп организации. 3ia задача шкже может быть отнесена к исследованиям, направленным па установление предельных возможностей систем деятельности, чго позволяет рассматривать ее в общей совокупности вопросов, критериев п оценок, связанных с гранично-деятелыюстной проблемашкоп.
Для выделения главных аспектов в гнои задаче в качестве исходных данных будем рассматривать изолированную систему деятельности, общесистемным эквивалентом которой може( служить замкнутая ГДС. Вследствие этого продуктивность такой системы будет полностью определяться только ее собственными потепциалыю-деятелыюстными возможностями, анализ зависимости которых от уровня системной организации показал следующее.
Деятелыюстные возможности системы находится в прямой зависимости от уровня системной организации. В первом приближении сказанное можно записать так:
![]()
где A (S) — деятельностная характеристика системы в целом; At (5,-) — деятельностная оценка по системной инварианте 5;; Aj — деятельностная оценка по /'-й качественной реализации системы S (или ее отдельных инвариант).
Выражение (5.47) может иметь прямую и обратную интерпретации. Если при создании снечемы i\ обладающей заданным уровнем снек'ма-тизации (определяется величинами i и /), затрачен определенный ресурс W (S), то в скрытой форме этот ресурс (для системы без потерь) распределен по всем системным инвариантам. Данную интерпретацию назовем прямой. Обратная интерпретация: если в системе S скрыты деятельностью возможности вида A (S), то именно их может реализовать система, если рассматривать ее с позиций оценки потенциалыю-деятельностных возможностей.
При этом отделяемый от системы продукт деятельности может быть получен (в отсутствие внешних источников) за счет саморагхода (па-пример, саморазрушения) системы. Б первом приближении взаимосвязь между системой деятельности и ее ироду к i ом может быть отобра-
жена соотношением гнперкомплсксных неопределенноеicii с дп)м> сомножителями:

где A (S) — полная деятельпостиая составляющая; A (R) — деятель-постная составляющая системного продукта (результата системной деятельности); t — время.
Из (5.47) можно сделать следующие выводы.
1. При прочих равных условиях, например при одних и тех же ис ходных данных по гиперкомплексности (числу элементов в системе), деятельностпые возможности системы с более высокой оргашппппеп выше, чем jiki.toi ичиой сисюмы с более низким орыпизацноиным уровнем.
2. Использование замкнутой ГДС в качестве системы деятельности с выдачей внешнею продукта, отчуждаемого от системы, ведет к необ ратимым системным потерям (в отсутствие внешнего источника ресур сов). Поэтому с целью сохранения спсюмы допельпоешьн! расход ее должен быть контролируемым и регламентируемым.
3. Исходная ГДС, рассматриваемая в кячестс- доятслы'остпоп, имеет наибольшую продуктивноегь в начальной фаче споет /ч-ироцстеа, что объясняемся ее максимальной разомкпутостыо в -л он (\,л,,г. По мере приближения к фазе стационарности (рост полноты замкнуто и) впеш- ная отдача системы падает, стремясь к нулю при достижении сопоянпя идеальной замкну 1ОСШ. В 'лом случае полностью нрекрлщлен'и шкчн- няя отдача, п система начинает работать в режиме самоиотреблення (сама на себя), переходя от дивергентной деятельности к ротационной. Без нарушения системной целостности получить отторгаемый от такой системы деятелыюстный продукт невозможно. Системная продуктив ность (с позиций внешнего потребления) имеет противоположные знаки в фазах развития и распада для ^-процесса одной и той же ГДС, рас сматриваемой в качестве системы деятельности.
Деятелыюстный эффем, определяемый уровнем системной организации, можно оцепить, если сравнить деятелыюстные возможности бессистемного (либо с минимально возможным уровнем системной организации) образования с возможностями высокоорганизованной системы дея 1елыюс| и (при одном н км же числе исходных элемсчм'Ш и прочих равных условиях). Разность между полученными оценками определит деятелыюстный эффект, обусловленный уровнем системной организации. Используя (5.47), запишем эту разность в виде АЛ (S(L2)) для систем S(" и S(2):

В выражении (5.50) индексы i п / начинаемся с шк|)ры 2, так как сравниваемые системы S(1) (низ fi уровень opi аппзацнн) и S<2) (выс шим уровень) совпадают в данном примере лишь по первой инварианте. Как следует из (5.50), именно оргашинцпоппо-дсяк'лыюешая состав ляющая вносит максимальным вклад в общий деятелыюстный потен циал исследуемой системы деиюлыюпн. При этом в конкретных практических ситуациях этот эффект может стать определяющим фак тором для развития реальных процессов. Например, толпа людей мо жет рассматриваться как бессистемное образование (либо как система с минимальным уровнем оркшпзацип). Хороню организованная груп па людей (система с высоким уровнем организации), находящаяся в этой толпе и значительно меньшая по численности, чем толпа, может полностью управлял, поведением и ликчмплмм киимч) бессистемного образования.
Важным практическим слечепшем ич оценки (5.50) может быть тракншка поручаемом рашоеш k.ik i нмемпо-деи к-лыюп пого резерва повышения производи слышен! труда (оффекгишюсти систем деятельности) в экономических, народнохозяйственных, социальных, производственных и других системах, включающих в свой состав большое число людей. При этом без привлечения каких-либо существенных технических средств и других дополнительных затрат, а лишь за счет оптимизации организационных cipyiuyp можно получить значительный эффект.
Для ориентировочной и бисiрои оценки оргапизациоино-деятель-ностного эффекта можно использовать полученное на основе анализа содержания выражений (5.47) п (5 50) следующее соотношение:
![]()
где k = kjki — обобщенный нормирующий коэффициент, содержащий качественную (k,) и количественную (к,) составляющие; A (S) — дея-тельностная оценка высокоорганизованной системы (с индексами i и /), определяемая по выражению (5.47); A (So) — оценка того же объекта в бессистемном состоянии.
В простейшем случае (при р.пшоресурспом обеспечении процесса ргализаичи всех системных инвариант по всем их качественным разно-видност:.м) значение коэффициентов в (5.51) можно принять равным единице.
Если вместо индексов i и / д.им опенка уровни енеюмпой организации (например, в виде величины о, рассмотренной в параграфе 4.3), то организационный э<|х|)ект для снек-мы деятельности, представленной выражением (1.1) и соотнесенной с ее бессистемным образованием, можно оценить следующим прпближишым соотношением:
![]()
где y — нормирующий коэффициент.
В соответствии с (5.52) имеем две крайние ситуации.
При ситуации, выраженной -лом форму -
той,![]() деятелыюстпые
возможности неорганизованной системы
сонпа-1ают с деятелыюстнымн возможностями
системообразующей среды.
деятелыюстпые
возможности неорганизованной системы
сонпа-1ают с деятелыюстнымн возможностями
системообразующей среды.
Выражение означает, что максимально
)ргапизованпая![]() система
имеет бесконечно большой потенциал
деятель-юстных
возможностей. Реализовать эту ситуацию
полностью, как эго ;ледует
из анализа выражения (1.1),
невозможно. Поэтому на практике
цеителыюстпые
оценки ограничиваются промежуточными
значениями. Например,
для а = 0,9 в (5.52) получим число десять
(десятикратное превышение
деятельпостных возможностей
высокоорганизованной системы
над ее бессистемным образованием).
система
имеет бесконечно большой потенциал
деятель-юстных
возможностей. Реализовать эту ситуацию
полностью, как эго ;ледует
из анализа выражения (1.1),
невозможно. Поэтому на практике
цеителыюстпые
оценки ограничиваются промежуточными
значениями. Например,
для а = 0,9 в (5.52) получим число десять
(десятикратное превышение
деятельпостных возможностей
высокоорганизованной системы
над ее бессистемным образованием).
Введя дополнительные условия и ограничения, можно перейти or ориентировочных опенок к более точным. I lanpiiMcp, переходя oi ана-лиза замкнутой ГДС к исследованию разомкнутой, можно учитывать влияние внешних воздействий на систему деятельности и компенсационные процессы за счет возобновления расходуемых системообразующих ресурсов, а также проводить одновременный анализ нескольких взаимодействующих систем деятельности и т. д.
