Лекції 4, 5

Скалярний, векторний та мішаний добутки векторів. Їх властивості та застосування.

План.

1. Скалярний добуток двох векторів. Властивості. Застосування.

2. Означення векторного добутку. Основні властивості даної операції та її застосування до розв’язування задач.

3. Поняття мішаного добутку трьох векторів. Властивості. Застосування до розв’язування задач.

1

. Розглянемо на площині або в просторі два довільні вектори та. Нехай.

К

утомміж векторами таназвемо кут між променямита. Причому з двох кутів, які при цьому утворюються, вибиратимемо той, який не перевищує, тобто (рис. 1).

Означення 1. Скалярним добутком векторів таназивають число.

Позначатимемо скалярний добуток символом або. Отже, згідно з означенням,=.

Розглянемо деякі властивості цієї операції.

Властивість 1. (комутативність скалярного множення).

Властивість 2. .

Властивість 3. , звідки(зауважимо, що виразназиваютьскалярним квадратом вектора ).

Доведення властивостей 1 – 3 безпосередньо випливають із означення скалярного добутку.

Два вектори домовимось називати ортогональними та записувати , якщо вони утворюють кут.

Властивість 4. Два ненульові вектори ортогональні тоді і тільки тоді, коли їхній скалярний добуток рівний нулю.

Для доведення скористаємось рівністю =. Якщо, то з неї випливає, що, тобто. Якщо, то, тому=0.

Властивість 5. Якщо >0, то кут міжвекторами тагострий. Якщо<0, то кут між векторами тупий.

Д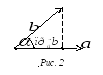оведення даної властивості випливає із означення скалярного добутку та властивостей функції.

Число називаютьпроекцією вектора на вектор

та позначають .(рис. 2). Тобто=.

Властивість 6. =.

Доведення властивості 6 випливає із означення скалярного добутку.

Знайдемо співвідношення для обчислення скалярного добутку у випадку, коли вектори та задані своїми координатами. Розглянемо вектори . Вважаючи їх не колінеарними, розглянемо трикутниктакий, що. За теоремою косинусів, де- кут між сторонамита. Оскількиі, то, використавши формулу, яка виражає довжину вектора через його координати, дістаємо

,

звідки

. (1)

Покажемо, що співвідношення (1) вірне також у випадку колінеарності векторів. Отже, нехай вектори таколінеарні та виконується векторна рівність. Запишемо її у координатній формі у виді рівностей,,.

При кутміжвекторами тарівний 0, тому

=++=.

При кутміжвекторами тарівний, тому

=++=,

тобто рівність (1) виконується для довільних векторів та

Використаємо рівність (1) для доведення інших властивостей скалярного добутку.

Властивість 7. (дистрибутивність скалярного множення).

Для доведення властивості 7 припустимо, що вектор задано у виді. Тоді. Із рівності (1) дістаємо

.

Властивість 8. для довільного числового множника .

Доведення даної властивості пропонуємо виконати самостійно.

Наступні властивості фактично повторюють деякі із попередніх, тільки подаються в координатній формі. Ми пропонуємо їх без доведення.

Властивість 9. Вектори таортогональні тоді і тільки тоді, коли

Якщо , то кут між векторамитагострий (тупий). При потребі кут між векторамитаможна обчислити, користуючись співвідношенням

. (2)

Властивість 10. Проекція вектора на векторобчислюється за формулою

. (3)

Зауважимо, що розглянуті властивості та одержані співвідношення мають місце також у випадку, коли кожний із векторів задається двома координатами. Зокрема, якщо задані вектори , то

, , _.

Розглянемо приклади задач, при розв’язуванні яких використовується операція скалярного множення.

Задача 1. У прямокутному трикутнику з катетами таобчислити кутміж медіаною, проведеною до гіпотенузи, та бісектрисою прямого кута.

Розв’язання. Нехай у прямокутному трикутнику - медіана, проведена до гіпотенузи. Зафіксуємо ортонормований базис, вибравши векторна променіта векторна промені. Тоді, оскільки, то. Виберемо один із векторів, які задають напрям бісектриси прямого кута, наприклад, вектор. Скориставшись формулою (1), дістаємо

.

Відповідь:.

Задача 2. Знайти ортогональну проекцію відрізка з кінцями в точках на пряму, яка проходить через точки.

Розв’язання. Введемо в розгляд вектори таі позначимо довжину шуканої проекції через. Тоді, скориставшись рівністю (3), дістаємо

.

Відповідь:.

Задача 3. Обчислити кут між мимобіжними діагоналлю куба та діагоналлю його бічної грані.

Розв’язання. Нехай - заданий куб. Знайдемо кут між його діагоналлюта діагоналлю бічної грані. Для цього введемо в розгляд прямокутну декартову систему координат, вибравши точкупочатком координат, а променівибравши за додатні напрямки осей відповіднота. Нехай ребро куба рівне 1. Тоді дістаємо,,,, звідки. Якщо шуканий кут позначити через, то.

Відповідь: .

Задача 4. (Теорема Стюарта). Сторони трикутника рівні та.Обчислити довжину відрізка, який сполучає вершину трикутника із точкою, вибраною на стороні, знаючи, що ця точка ділить сторону на відрізки з довжинамита.

Розв’язання. Нехай у трикутнику ,,,- шуканий відрізок. Очевидно, що. Тоді

, ,

звідки

, .

Помноживши першу з одержаних рівностей на , а другу – ната додавши одержані співвідношення, дістаємо

,

оскільки вираз у круглих дужках рівний , як сума двох векторів із однаковими довжинами та протилежними напрямками. Рівність

виражає зміст теореми Стюарта та дає відповідь на поставлену задачу.

2. Нехай у просторі задано два вектори та. Знайдемо, використовуючи дані вектори, третій вектор, який задовольняє певним умовам – так званий векторний добуток векторівта. Оскільки нам доведеться користуватись поняттямоднакової орієнтованості двох трійок векторів, то введемо наступне означення.

Означення 2. Нехай задана впорядкована трійка некомпланарних векторів , відкладаних із спільного початку. Із кінця третього вектора розглядається поворот першого з них до суміщення з напрямком другого вектора найкоротшим шляхом (тобто на кут, який не перевищує). Якщо цей поворот здійснюється за годинниковою стрілкою, то кажуть, що целіво орієнтована трійка векторів, а коли проти – право орієнтована трійка. На рисунку 4_а зображена ліво орієнтована, а на рисунку 4_б – право орієнтована трійка векторів .

Рис. 4_а Рис. 4_б

Означення 3. Дві впорядковані трійки векторів таназиваються однаково орієнтованими, якщо вони одночасно право або ліво орієнтовані.

Означення 4. Вектор називаєтьсявекторним добутком векторів та, якщо він задовольняє наступні умови:

1. вектор ортогональний до кожного з векторівта;

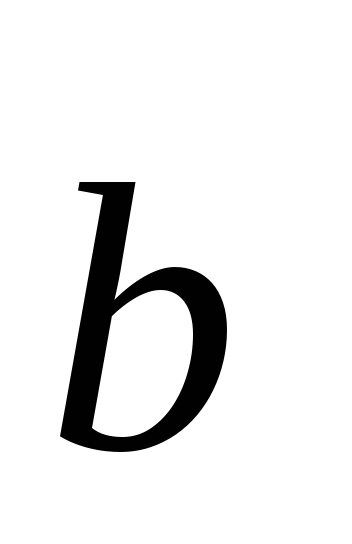2. , де - кут між векторамита;

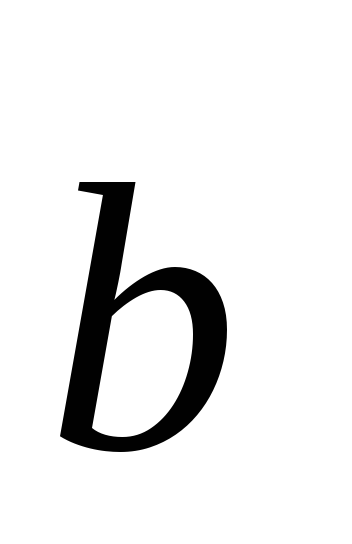3. трійки векторів таоднаково орієнтовані (рис. 5).

Векторний добуток векторів тапозначають символомабо. Безпосередньо з означення випливають перші властивості векторного множення.

Властивість 1. =-(антикомутативність векторного множення).

Властивість 2. Довжина вектора дорівнює площі паралелограма, побудованого на векторахта.

Властивість 3. Векторний добуток двох ненульових векторів рівний нульовому вектору тоді і тільки тоді, коли вони колінеарні.

Доведення властивості 1 фактично випливає з третьої умови означення, оскільки перші дві умови виконуються одночасно для векторів та. При перестановці у векторному добутку двох множників поворот першого з них до суміщення з напрямком другого вектора найкоротшим шляхом здійснюється в протилежному напрямку. Оскільки векторитаколінеарні (обидва одночасно перпендикулярні до векторівта), мають однакові довжини та протилежно напрямлені, то=.

Властивість 2 випливає із формули, яка виражає площу паралелограма через дві сторони та кут між ними та відома читачам із шкільного курсу геометрії.

Щоб довести властивість 3 зауважимо, що якщо вектори таколінеарні, то кут між ними рівний 0 або. В обох випадках, оскільки, то. Навпаки, якщо=, то, оскільки. Тому векторитаколінеарні.

Для формулювання та доведення інших властивостей векторного добутку виведемо співвідношення, яке дозволяє знаходити координати вектора через координати векторівта.

Нехай в базисі векторитазадані своїми координатами:,. Вважатимемо, що=. Згідно з умовою 1) означення маємота, томута. Одержані рівності запишемо у виді системи

,

розв’язуючи яку, дістаємо ,,, де- довільне дійсне число. Для відшукання значеннявикористаємо другу умову означення:

=

=

=. (5)

З іншого боку

. (6)

Легко перевірити, що підкореневі вирази у записах (5) та (6) рівні, тому , або. Щоб вибрати з двох одержаних значеньпотрібне, використаємо відомий з курсу лінійної алгебри факт, що визначник матриці переходу від одного базису до іншого відмінний від нуля. При цьому базиси будуть однаково орієнтовані тоді і тільки тоді, коли визначник додатній. Вважатимемо, що векторитане колінеарні, тому трійка векторівтаутворює базис. У випадку, коли векторитаколінеарні,, тому необхідність визначення знаку числавідпадає. Знайдемо визначник матриці, складеної із координат векторівта, а також вимагатимемо, щоб він був додатнім. Дістаємо

.

Звідси випливає, що число додатне, тому . Таким чином,

(, ,).

Для одержаного вектора часто вибирають іншу, більш зручну для запам’ятання форму запису у виді визначника:

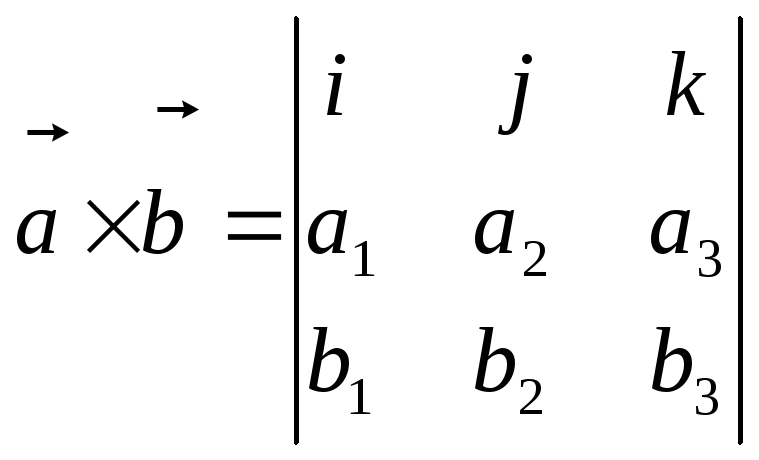. (7)

У цьому випадку координати вектора обчислюють, як алгебраїчні доповнення до елементів першого рядка.

Перейдемо до вивчення інших властивостей та застосувань векторного добутку.

Властивість 4. .

Властивість 5. (дистрибутивність векторного множення).

Доведення властивостей 4 та 5 випливає з відомих властивостей визначників.

Властивість 6. Площу трикутника, вершини якого розташовані в точках ,,, можна обчислити за формулою

. (8)

Справді, оскільки площа паралелограма, побудованого на векторах та, дорівнюєі

,,

то, скориставшись рівністю (7), дістаємо

=.

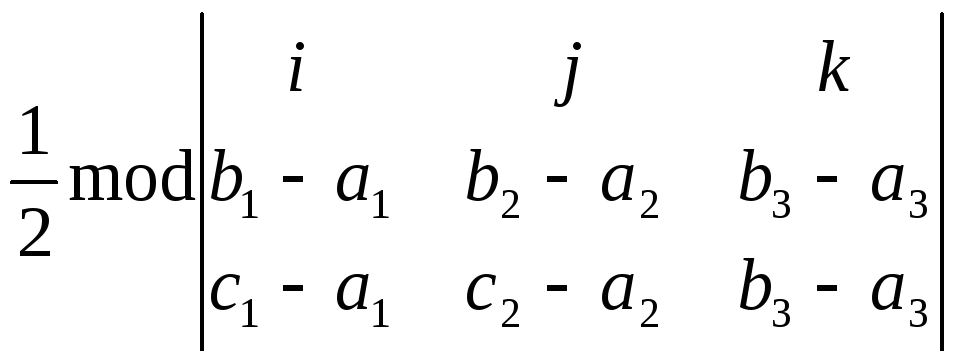Наслідок. Якщо вершини трикутника знаходяться в точках ,,, то площу трикутника можна обчислити за формулою

.

Для доведення розглянемо точки ,,в тримірній системі координат. Скориставшись рівністю (8), дістаємо

=,

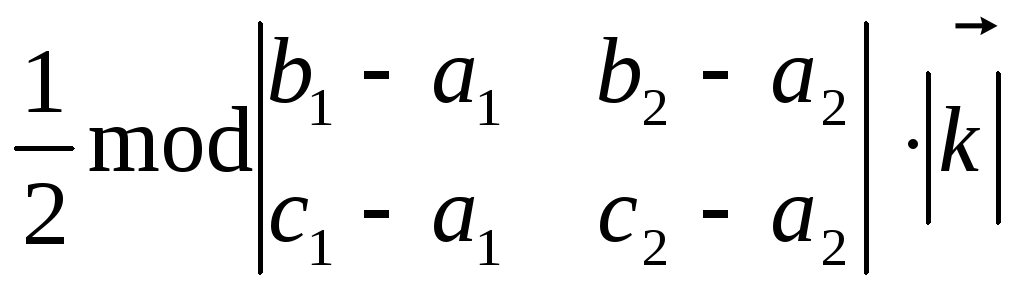
що і потрібно було довести.

Розглянемо приклади деяких задач.

Задача 5. Обчислити площу паралелограма, побудованого на векторах та, знаючи, що, а кут між векторамитарівний.

Розв’язання. На основі доведених властивостей дістаємо ()()=.Тоді

=.

Відповідь: 66.

Задача 6. Обчислити відстань від початку координат до прямої, яка проходить через точки.

Розв’язання. Шукану відстань знайдемо як висоту трикутника , опущену із вершини. Для цього спочатку обчислимо площутрикутника . Використовуючи співвідношення (7), дістаємо ==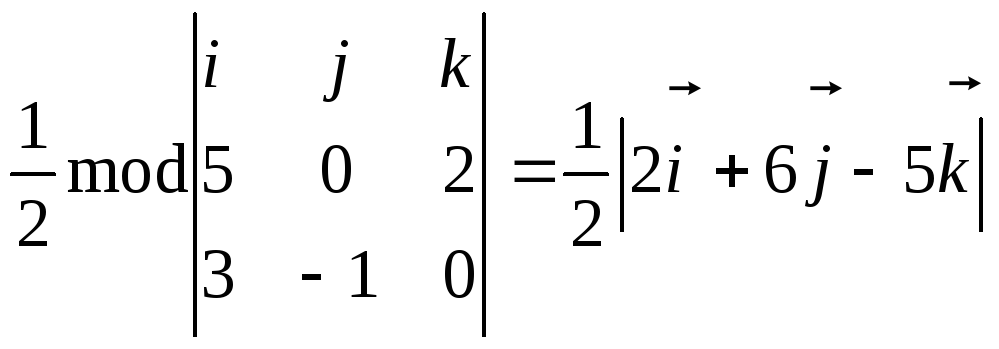. Тепер, оскільки, то.

Відповідь:.

Задача 7. У трикутній піраміді перпендикулярно до кожної грані назовні відносно піраміди проведено вектори, довжина кожного з яких дорівнює площі відповідної грані. Обчислити їхню суму.

Розв’язання. Нехай - задана піраміда,, а також- вектори, які задовольняютьумову задачі та проведені до граней відповідно (рис. 5). Обчислимо вектори, як половини векторних добутків векторів, напрямлених по ребрах піраміди. Орієнтацію трійок векторів вибираємо праву. Дістаємо

,

Рис. 5

,

.

Очевидно, що сума знайдених векторів дорівнює . Відповідь:.

3. Розглянемо три довільні вектори таз векторного просторута введемо означення ще одної операції над векторами – так званий мішаний добуток.

Означення 5. Мішаним добутком векторів таназивається скалярний добуток векторана вектор, який є векторним добутком векторівта.

Позначатимемо мішаний добуток векторів тасимволом. Отже, згідно з означенням,. Зауважимо, що мішаний добуток векторівтає число. Дослідимо властивості введеної нами нової операції. Для цього спочатку знайдемо співвідношення, яке виражає мішаний добуток через координати векторів. Нехай відомо, що,,. Тоді, оскільки, то, що зручно записувати у вигляді визначника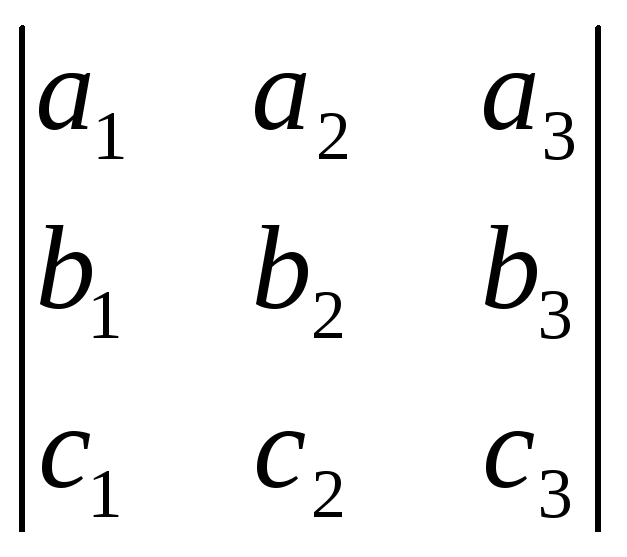. Отже,

(9)

Циклічною перестановкою(перестановкою по колу) скінченої впорядкованої множини елементів називають перестановку, коли кожний елемент займає місце наступного, а останній – першого, або навпаки: кожний елемент займає місце попереднього, а перший–останнього.

Властивість 1. Циклічна перестановка не змінює величини мішаного добутку, тобто виконуються рівності .

Властивість 2. , де- довільне число.

Властивість 3. +.

Доведення перерахованих властивостей випливає з властивостей визначників. Зокрема, в першому випадку доводиться двічі міняти місцями рядки визначника, що не змінює його величини. У другому випадку з одного із рядків перед знак визначника виноситься сталий множник , наякий множиться кожнакоординатавектора.У третьому випадку перший рядок визначника є сумою двох рядків, що дозволяє записати цей визначник у вигляді суми двох визначників, у кожному з яких ці рядки записані окремо.

Зауважимо, що з рівності випливає, що мішаним добутком векторівтаможна назвати також скалярний добуток векторного добутку векторівтана вектор.

В

ластивість 4. Об’єм паралелепіпеда, побудованого на векторах та, дорівнює модулю мішаного добутку цих векторів.

Доведення. Згідно з означеннями мішаного та скалярного добутків дістаємо , де- кут між векторамита (рис.6).

О

Рис. 6

скільки числовиражає площупаралелограма, побудованого на векторахта, а добутокрівний висоті паралелепіпеда, якщо кутгострий та, якщо- тупий, то об’єм паралелепіпеда.

Наслідок 1. Три вектори компланарні тоді і тільки тоді, коли їхній мішаний добуток рівний нулю.

Справді, якщо три вектори компланарні, то , отже,. Навпаки, якщо, то, тому, тобто вектори компланарні.

Наслідок 2. Три вектори ,,лінійно залежні тоді і тільки тоді, коли виконується умова.

Зауважимо, що наслідок 2 можна використовувати у тих випадках, коли потрібно довести, що вектори таутворюють базис простору. Для цього достатньо показати, що виконується умова.

Наслідок 3. Нехай вершини трикутної піраміди розташовані в точках . Тоді її об’ємможна обчислити за формулою

.

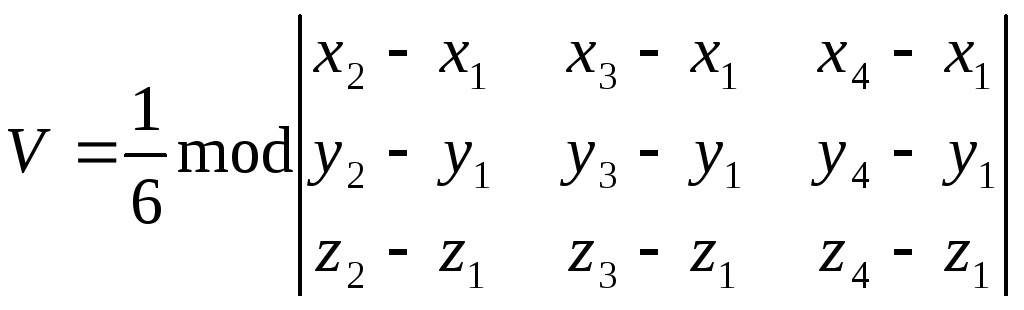Доведення цього твердження випливає з того, що об’єм паралелепіпеда, побудованого на векторах ,та, як на ребрах, дорівнює

, а об’єм піраміди становить від нього частину.

Наведемо приклади розв’язання окремих задач.

Задача 8. Обчислити об’єм паралелепіпеда, побудованого на векторах, якщо об’єм паралелепіпеда, побудованого на векторахта, рівний 5.

Розв’язання. Використавши властивості 2, 3 та 4, дістаємо

. Тому . Зауважимо, що в процесі обчислень були опущені деякі доданки, оскільки вони являють собою мішані добутки компланарних векторів і рівні нулю.

Відповідь: 5.

Задача 9. Вивести формулу для обчислення висоти трикутної піраміди, побудованої на векторахта. Вважається, що висота проведена з вершини, яка є спільним початком заданих векторів.

Розв’язання. З шкільного курсу геометрії відомо, що , де- об’єм піраміди, а- площа її основи. З попереднього. Для обчислення площі основи візьмемо два вектори, які напрямлені по сторонах трикутника, який лежить в основі, нехайі, та скористаємось векторним добутком. Маємо

.

Підставляючи одержані значення тау формулу для обчислення висоти, дістаємо шуканий результат.

Відповідь:.

Задача 10. По двох мимобіжних прямих ковзають два відрізки сталої довжини. Як змінюється об’єм трикутної піраміди, яка утворюється після сполучення кінців відрізка?

Розв’язання. Нехай заданими відрізками є відрізки та, які після переміщення переходять у рівні відрізкита. Введемо векторні позначення: ,. Тоді об’єм пірамідибуде, а об’єм піраміди-. Оскільки(тутта- деякі числові коефіцієнти), то

.

Отже, об’єм піраміди не змінюється.