30

Прикарпатський національний університет імені Василя Стефаника

Кафедра алгебри та геометрії

Р. І. Собкович

Лекції з аналітичної геометрії

(для студентів, які навчаються за спеціальностями «прикладна математика» та «інформатика»)

Івано-Франківськ

2010

Зміст

Лекція 1. Вектори. Лінійні операції над векторами.

План.

1. Поняття вектора. Основні означення. Колінеарні та компланарні вектори.

2. Додавання та віднімання векторів. Властивості даних операцій.

3. Множення вектора на скаляр. Властивості.

4. Приклади розв’язання задач.

Лекція 2. Лінійна залежність та незалежність векторів.

План.

1.Поняття лінійної залежності та незалежності векторів. Основні теореми.

2. Базис системи векторів.

3. Координати вектора. Дії над векторами в координатній формі.

4. Ортонормовані базиси. Довжина вектора.

5. Приклади розв’язання задач.

Лекція 3. Загальна афінна та прямокутна декартова системи координат. Координати точки. Поділ відрізка у даному відношенні.

План.

1. Поняття загальної афінної системи координат. Координати точки.

2. Прямокутна декартова системи координат. Відстань між двома точками.

3. Поділ відрізка у даному відношенні.

4. Теорема Чеви.

5. Приклади.

Лекції 4, 5. Скалярний, векторний та мішаний добутки векторів. Їх властивості та застосування.

План.

1. Скалярний добуток двох векторів. Властивості. Застосування.

2. Означення векторного добутку. Основні властивості даної операції та її застосування до розв’язування задач.

3. Поняття мішаного добутку трьох векторів. Властивості. Застосування до розв’язування задач.

Лекція 6. Зв'язок між координатами точки в різних системах координат. Поняття порядку лінії та поверхні.

План.

1. Зв'язок між координатами точки в різних системах координат на площині.

2. Зв'язок між координатами точки в різних системах координат у тривимірному просторі.

3. Поняття порядку лінії.

4. Поняття порядку поверхні.

5. Приклади.

Лекція 7. Пряма на площині. Різні способи задання прямої на площині.

План.

_{1. Геометричні образи рівнянь першого степеня з двома змінними.}

_{2. Різні способи задання прямої на площині.}

_{3. Частинні випадки загального рівняння прямої.}

_{4. Приклади.}

Лекція 8. Взаємне розташування прямої та деяких геометричних фігур.

План.

1. Відстань від точки до прямої.

2. Взаємне розташування кола та прямої.

3. Взаємне розташування двох прямих на площині. Умова паралельності. Кут між двома прямими. Умова перпендикулярності.

4. Відстань між двома паралельними прямими.

5. Геометричний зміст знаку виразу .

6. Пучок прямих.

7. Задачі.

Лекція 9. Різні способи задання прямої та площини в просторі.

План.

1. Геометричні образи рівнянь першого степеня з трьома змінними.

2. Різні способи задання площини.

3. Загальне рівняння площини та його частинні випадки.

4. Різні способи задання прямої в просторі.

5. Задачі.

Лекція 10. Відстань від точки до площини. Взаємне розташування площин.

План.

1. Відстань від точки до площини.

2. Геометричний зміст знаку виразу .

3. Взаємне розташування двох площин. Умова паралельності. Кут між двома площинами. Умова перпендикулярності.

4. Відстань між двома паралельними плошинами.

5. Взаємне розташування трьох площин.

6. Приклади.

Лекція 11. Взаємне розташування прямої та площини. Дві прямі в просторі

План.

1. Пряма і площина в просторі. Кут між прямою та площиною.

2. Взаємне розташування двох прямих в просторі.

3. Рівняння спільного перпендикуляра. Відстань між двома мимобіжними прямими.

4. Задачі.

Лекція 12. Канонічні рівняння еліпса, гіперболи та параболи.

План.

1. Поняття загального рівняння другого порядку.

2. Означення еліпса. Канонічне рівняння. Вирази для фокальних радіусів.

3. Означення гіперболи та її канонічне рівняння. Вирази для фокальних радіусів.

4. Означення параболи та її канонічне рівняння.

5. Приклади.

Лекції 13, 14. Вивчення властивостей еліпса, гіперболи та параболи за канонічними рівняннями.

План.

1. Найпростіші властивості еліпса та його зображення.

2. Найпростіші властивості гіперболи та її зображення.

3. Властивості та зображення параболи.

4. Поняття ексцентриситету.

5. Поняття директрис. Директоріальна властивість ліній другого порядку.

6. Дотична до лінії другого порядку.

7. Оптичні властивості ліній другого порядку.

Лекція 15. Поняття полярних координат. Рівняння конічних перерізів у полярних координатах.

План.

1. Поняття полярних координат.

2. Зв'язок між полярними та прямокутними декартовими координатами.

3. Відстань між двома точками та площа трикутника у полярних координатах.

4. Рівняння деяких ліній у полярних координатах.

5. Рівняння конічних перерізів.

6. Історія виникнення назви конічних перерізів.

Лекція 16. Деякі поверхні другого порядку. Їхні канонічні рівняння, властивості та зображення.

План.

1. Загальне рівняння поверхні другого порядку. Сфера та її рівняння.

2. Дослідження поверхні другого порядку за допомогою плоских перерізів.

3. Еліпсоїд. Властивості. Зображення.

4. Однопорожнинний гіперболоїд. Властивості. Зображення.

5. Двопорожнинний гіперболоїд. Властивості. Зображення.

6. Еліптичний параболоїд. Властивості. Зображення.

7. Гіперболічний параболоїд. Властивості. Зображення.

Лекція 17. Циліндричні та конічні поверхні. Поверхні обертання. Прямолінійні твірні поверхонь другого порядку.

План.

1. Поняття циліндричної поверхні. Рівняння циліндричних поверхонь. Приклади.

2. Поняття конічної поверхні. Рівняння конічних поверхонь.

3. Поверхні обертання.

4. Прямолінійні твірні поверхонь другого порядку.

5. Приклади розв’язання задач.

Лекція 18. Загальне рівняння лінії другого порядку.

План.

1. Поняття загального рівняння лінії другого порядку.

2. Перетин лінії з прямою. Частинні випадки.

3. Центр лінії.

4. Рівняння дотичної та нормалі.

Лекції 19 – 20. Деякі властивості ліній другого порядку та їх застосування до зображення ліній.

План.

1. Теорема про середини паралельних хорд лінії другого порядку.

2. Спряжені напрямки та спряжені діаметри.

3. Спряжені напрямки нецентральних ліній.

4. Головні напрямки та головні діаметри. Рівняння осей симетрії.

5. Рівняння асимптот лінії другого порядку.

6. Орієнтовна схема вивчення властивостей лінії другого порядку.

7. Приклади побудови ліній за їхніми рівняннями.

Лекція 21 .Спрощення рівняння лінії другого порядку за допомогою геометричних перетворень.

План.

1. Спрощення рівняння лінії за допомогою паралельного перенесення системи координат.

2. Спрощення рівняння лінії за допомогою повороту системи координат.

3. Застосування геометричних перетворень для побудови ліній другого порядку.

Лекція 22. Інваріанти рівняння кривої другого порядку. Застосування інваріантів для побудови ліній та їх класифікації.

План.

1. Інваріанти рівняння лінії.

2. Характеристичне рівняння.

3. Класифікація ліній другого порядку.

4. Застосування інваріантів для побудови ліній другого порядку.

Лекція 23. Загальне рівняння поверхні другого порядку.

План.

1. Поняття загального рівняння поверхні другого порядку.

2. Перетин поверхні з прямою. Частинні випадки.

3. Центр поверхні.

4. Рівняння дотичної площини та нормалі.

Лекція 1

Вектори. Лінійні операції над векторами.

План.

1. Поняття вектора. Основні означення. Колінеарні та компланарні вектори.

2. Додавання та віднімання векторів. Властивості даних операцій.

3. Множення вектора на скаляр. Властивості.

4. Приклади розв’язання задач.

1. Із курсу елементарної фізики відомо, що деякі фізичні величини, зокрема такі, як довжина, площа, об’єм, температура, маса, густина, відстань виражаються одним числом, яке характеризує відношення цієї величини до відповідної одиниці вимірювання. Такі величини називають скалярними. Для характеристики ряду інших величин (сили, переміщення, швидкості, прискорення і ін.) одного числа недостатньо. Крім кількісної оцінки вони характеризуються також направленістю в просторі. Такі величини називають векторними. Абстрагуючись від конкретних фізичних величин, введемо математичне поняття геометричного вектора або просто вектора.

Означення 1. Вектором називається напрямлений відрізок.

Вектор визначається впорядкованою парою точок. Перша з них називається початком, друга – кінцем вектора. Якщо початком вектора є точка , а кінцем точка, то його позначають символом. Іноді використовують позначення у вигляді малої букви латинського алфавіту (наприклад,). На рисунку вектор зображають відрізком із стрілкою в кінці вектора.

Вектор, початок та кінець якого співпадають, називається нульовим і позначається грецькою буквою (тета).

Основними характеристиками вектора є його довжина та напрям.

Довжиною (модулем) вектора називають довжину відрізка, яким він зображається. Позначають довжину вектора символом Наприклад,. Якщо довжина вектора рівна одиниці, то його називаютьодиничним або ортом. Очевидно, що .

Під напрямом вектора розуміють напрям променя. Нульовому вектору присвоюють довільний напрям.

Означення 2. Два вектори називають колінеарними, якщо вони паралельні деякій прямій.

Означення 3. Три вектори називають компланарними, якщо вони паралельні деякій площині.

Означення 4. Два колінеарних вектори називають однаково (протилежно) напрямленими, якщо вони лежать в одній півплощині (в різних півплощинах) відносно прямої, яка сполучає їхні початки. Якщо два вектори талежать на одній прямій, то їх називають однаково напрямленими, якщо всі точки одного із променівабоналежать іншому. Якщо жоден із променівтацілком не належить іншому, то вектоританазивають протилежно напрямленими.

Однаково напрямлені вектори тапозначають символом. Протилежно напрямлені векторитапозначають.

Два вектори, які мають однакові довжини та протилежні напрямки, називають протилежними. Протилежним до вектора є вектор. Вектор, протилежний до, позначають символом. Доцільність саме такого позначення стане зрозумілою після введення у пункті3 означення добутку вектора на число.

Означення 5. Два вектори називають рівними, якщо вони однаково напрямлені та мають рівні довжини.

Умову рівності векторів тазаписують так:. Від будь-якої точки площини чи простору можна відкласти вектор, рівний даному і причому тільки один. На рисунку 1 зображено ромб, на якому показані рівні вектори=та протилежні векториі. Векториі, незважаючи на рівність довжин відрізківта, не рівні, оскільки вони мають різні напрямки.

2.Введемо означення лінійних операцій над векторами. Під лінійними операціями над векторами розуміють дії додавання векторів, а також множення їх на числа.

Означення 6. Сумою векторів таназивають вектор, проведений з початку векторадо кінця векторапри умові, що кінець вектораспівпадає з початком вектора(рис.2).

Суму векторів тапозначають символом. Для довільних трьох точокта, згідно із означенням суми векторів, виконується рівність.

Означений таким чином спосіб додавання векторів називають “правилом трикутника”.

Якщо вектори тавідкласти із спільного початку та на одержаних відрізках, як на сторонах, побудувати паралелограм, то вектор, який співпадає з діагоналлю та має початок у спільному початку даних векторів, буде їхньою сумою (рис.3). Такий спосіб знаходження суми векторів називається“правилом паралелограма” Очевидно, що додавання векторів за “правилом трикутника” та “правилом паралелограма” дають у результаті один і той же вектор.

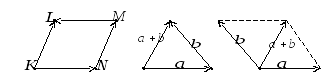
Рис. 1 Рис. 2 Рис. 3

Послідовне додавання векторів …, тау результаті дає вектор. В математиці такі суми записують за допомогою великої грецької букви(сигма). Зокрема, попередню рівність можна записати у виді

.

Якщо , то це означає, що точкитаспівпадають, тобто многокутникзамкнутий.

Очевидно, що для довільного трикутника виконується рівність. Навпаки, якщо дано три векторита, серед яких є хоча б два неколінеарних, то із них можна утворити трикутник, якщо виконується рівність, або коли один із векторів є сумою двох інших.

Зупинимося на деяких властивостях операції додавання векторів. Зокрема,

1) (комутативність додавання або переставна властивість);

2) (асоціативність додавання або сполучна властивість);

3) ;

4) .

Доведення властивості 1) випливає із рисунка 3.

Для доведення властивості 2) покладемо . Тоді

, ,,,

тобто .

Доведення властивостей 3) та 4) очевидне.

Означення 7. Різницею векторів таназивають вектор, який є розв’язком рівняння.

Такий розв’язок існує і єдиний. Справді, розглянемо вектор . Підставляючи його в рівняннята використовуючи властивості 2), 4) і 3), переконуємось, що він є розв’язком рівняння.

Різницю векторів тазаписують у виді. Отже, запис, згідно з означенням різниці векторів, означає, що. Звідси випливає спосіб побудови вектора, який є різницею векторівта, а саме: векторитавідкладають із спільного початку, а потім, сполучивши кінці векторів,та вибравши напрям шуканого вектора від кінцядо кінця вектора, одержують вектор(рис. 4). Очевидно, що різницю векторівтаможна одержати, додаючи векторита(рис. 5), тобто для різниці векторів виконується рівність.

Рис. 4 Рис. 5

3. Нехай заданий деякий вектор та дійсне число.

Означення 8. Добутком вектора на число називають вектор, який задовольняє наступні умови:

1) довжина цього вектора ,

2) , якщота, якщо.

При згідно з пунктом 1) означення, тому результатом множення довільного вектора на 0 є нульовий вектор. Добуток векторана числозаписують у виді.

Множення вектора на число має ряд властивостей, зокрема такі:

1) ;

2) ;

3) ;

4) ;

5) (асоціативність множення відносно числових множниківта);

6) (дистрибутивність множення відносно числового множника);

7) (дистрибутивність множення відносно векторного множника).

Доведення властивостей 1) – 4) очевидне. Для доведення властивості 5) потрібно розглянути наступні випадки: а) ; б); в); г); д) одне з чиселl i t або обидва ці числа дорівнюють нулю. У випадку а), оскільки , то. Враховуючи те, що, дістаємо, що. Отже,. Очевидно, що, тобто векторитаспівнапрямлені. Рівність їхніх довжин випливає із рівності. Згідно з означенням рівності векторів властивість 5) у випадку а) доведена. Випадки б), в) та г) розглядаються аналогічно. У випадку д) рівність 5) виконується, оскільки обидві частини рівності є нульовими векторами. 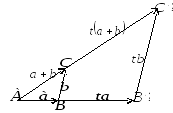Властивість 6) випливає з подібності трикутниківта(див. рис. 6 прита рис. 7 при). Доведення властивості 6) приочевидне.

Рис. 6 Рис. 7

Для доведення властивості 7) потрібно розглянути випадки, коли числа таl одного знаку (обидва додатні або від’ємні ) або різних знаків. Нехай та. Тодіі. Векторитапротилежно напрямлені, а також. ТомуВектормає напрям вектора, тобто співнапрямлений з вектором. Отже, в обох частинах рівності 7) маємо співнапрямлені вектори однакової довжини, тобто ці вектори рівні.

Аналогічно розглядається випадок та випадок, коли. Якщо одне із чиселt або l рівне нулю, або вони обидва дорівнюють нулю, то рівність 7) очевидна.

Зауважимо, що якщо , то вектородиничний і має напрям вектора. Справді,

.

4. Наведемо приклади розв’язання задач.

Задача 1. Довести, що точка є центром ваги трикутника(точкою перетину медіан) тоді і тільки тоді, коли виконується рівність.

Д

оведення. Нехай точка є точкою перетину медіанта(рис. 8).Тоді, де– діагональ паралелограма. Оскільки точка– середина відрізківта, то. За відомою властивістю медіан трикутника, тому. Отже,

Рис. 8

.

Навпаки, нехай виконується рівність , тобто. Тоді, де– середина відрізка. З рівностівипливає, що точкиталежать на одній прямій, а також, що– медіана трикутника. Оскільки, то точкає точкою перетину медіан.

Задача 2. У п’ятикутнику ABCDE точки K,L,M,N – середини відповідно сторін AB, BC, CD та DE, а точки R і S – середини відрізків KM та LN. Довести, що та(рис. 9).

Д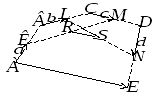оведення. Введемо позначення: . Тоді

. Знайдемо вектор .

. Оскільки та, то

Рис. 9

. Із одержаної рівності випливає, що та.

Задача 3. В опуклому чотирикутнику точкита– відповідно середини сторіні. Довести, що якщо, то.

Доведення. Очевидно, що та. Додавши одержані рівності, дістаємо, звідки. Але за умовою. Рівністьможлива тільки тоді, коли векторитаспівнапрямлені, тобто, коли відрізкитапаралельні. Отже,.