10.Обернений простір. Обернена гратка. Зони Бріллюена.

На даному етапі розгляду періодичних структур целесообразно, нарешті, ввести поняття зворотного простору і зворотної решітки. Точно так само як будь-яку величину, вимірюв-няющая в часі, можна представити у вигляді суми фур'є-компонент у частотній області, так і будь-яку просторових характеристику кристала можна записати у вигляді суми компонент у фур'є-просторі, або зворотному пространстве. Для ідеального монокристала (що представляє собою набір повторюваних в тривимірному просторі іден ¬ тичних блоків) зворотна решітка в фур'є-просторі образуется нескінченним безліччю точок, періодично расположені в тривимірному просторі, відстані між якими обернено пропорційні відстаням між плоскостями в прямій решітці . Тому очевидно, що відстані в зворотній решітці можна пов'язати з умовою дифракції.

Оскільки в реальному просторі вектори мають розмірність довжини, у зворотному просторі вектори мають розмірність (довжина) -1. Вектори зворотного простору можна співпоставити з хвильовими векторами збуджень (таких, як фотони, коливання грати або рухомі вільні електрони). Множення кожної координати на Й перетворює об ¬ ратну простір в простір імпульсів. Поняття про ратної решітки ми будемо часто використовувати у наступних розділах (гл. 2-4). У цій же главі ми розглянемо насамперед питання про те, які нові переваги дає поняття оберненої решітки з точки зору умови дифракції Брегга.

(1.38)

Нехай а, Ь і с - примітивні вектори трансляції трьохмірної решітки в реальному просторі. Тоді основні вектори оберненої гратки можна визначити наступним чином:

Можна записати наступні співвідношення для векторів прямого і зворотного грат:

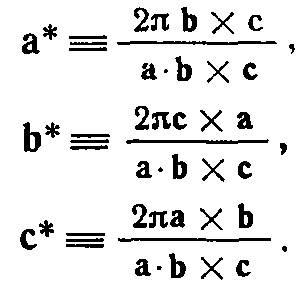
Зворотне перетворення до прямої решітці можна записати аналогічно виразами

зони Бріллюена

Якщо пряма грати строго періодична, то зворотна решітка, тобто безліч точок, які відповідають умові (1.43), також періодична і нескінченна. Однак у тих завданнях фізики твердого тіла, де зручно використовувати уявлення обратної решітки, досить буває обмежитися кінцевим об 'ємом зворотного простору, або до-простору. Так йде справа в задачах, пов'язаних з визначенням дисперсійних законів для електронів або елементарних збуджень у кристал.

Першу зону Бріллюена визначають як область в обрат ¬ ном просторі, навколишнє один з вузлів зворотного решітки і обмежену набором площин, що проходять через середини векторів, що з'єднують у зворотній решітці дану точку з її найближчими сусідами. На рис. 1.52 показана зона Бріллюена для двовимірної косокутній решітки. Аналогічно визначається зона Бріллюена і в тривимірних гратах (за ¬ дача 1.19). Будь-якій точці Л '(до') у зворотному просторі відповідає точка А (к) у першій зоні Бріллюена, так що виконується співвідношення

2Частина зворотного простору для двовимірної косокутній решітки

11.Електронний газ у металахТермодинамічні властивості електронного газу в металах.

Нам необхідно розрахувати властивості основного стану системи із N електронів, що знаходяться в об’ємі V. Оскільки електрони не взаємодіють один з одним, основний стан цієї системи можна знайти вичисливши спочатку рівні енергії окремого електрона в об’ємі V і заповнюючи потім всі рівні знизу вверх у відповідності з принципом Паулі, який забороняє двом електронам одночасно займати один електронний рівень.

Фермі-газ утворений з ферміонів — частинок, які не можуть перебувати в станах із однаковими квантовими числами. Ферміони підкоряються статистиці Фермі-Дірака. Прикладом ідеального Фермі-газу є електрони в металах.

Рівняння стану Фермі-газу записується в параметричному вигляді

,

,

де параметром є величина хімічного потенціалу μ. Інші позначення в цій формулі: g — фактор виродження (2 для електронів, у яких спін 1/2), —зведена стала Планка. Міняючи параметр μ і обчислюючи інтеграли, можна побудувати залежність тиску від об'єму для будь-якої температури й будь-якого числа частинок.

При високих температурах Фермі-газ поводить себе аналогічно класичному газу. Перша поправка до рівняння стану має вигляд

.

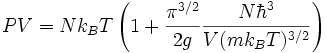Таким чином, тиск при тому ж об'ємі для Фермі-газу збільшується завдяки зумовленому принципом Паулі відштовхуванню між частками.

При низьких температурах та високих густинах Фермі-газ стає виродженим, і втрачає схожість із класичним ідеальним газом. Умова виродження задається нерівністю

.

Температура називаєтьсятемпературою виродження.

При виконанні цієї умови рівняння стану ідеального електронного газу має вигляд:

.

Це рівняння справедливе також і для абсолютного нуля температури. Тиск виродженого Фермі-газу не залежить від температури.