
- •1. Різні способи задання прямих та пллощин в просторі. Взаємне розташування двох прямих, прямої та площини. Пряма в просторі
- •Дві прямі в просторі Задані дві прямі:
- •Непорожню підмножину h групи g називають підгрупою цієї групи, якщо н є групою відносно бінарної операції, визначеної в групі g.
- •3. Системи лінійних рівнянь та точні методи їх розв’язування
- •4. Лінійна залежність та ранг системи векторів.
- •6. . Лінійні оператори дійсних векторних просторів,їх матриці ранг і дефект.
- •7) Власні вектори та власні числа лінійних операторів.
1. Різні способи задання прямих та пллощин в просторі. Взаємне розташування двох прямих, прямої та площини. Пряма в просторі
Нехай
задана точка
![]() і напрямний вектор
і напрямний вектор
Скласти
рівняння промої, що проходить через
точку
![]() і яка // вектору
і яка // вектору![]() .
М(x,y,z)
біжуча точка.
.
М(x,y,z)
біжуча точка.
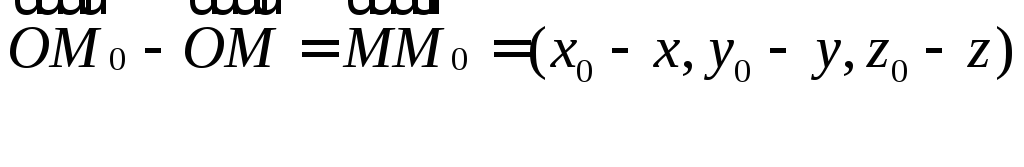 Якщо
точка М(x,y,z)
належить прямій d
то вектори
Якщо
точка М(x,y,z)
належить прямій d
то вектори
![]() колінеарні, а іхні координати пропорційні
.
колінеарні, а іхні координати пропорційні
.![]()
![]() – канонічне рівняння прямої в просторі.
– канонічне рівняння прямої в просторі.
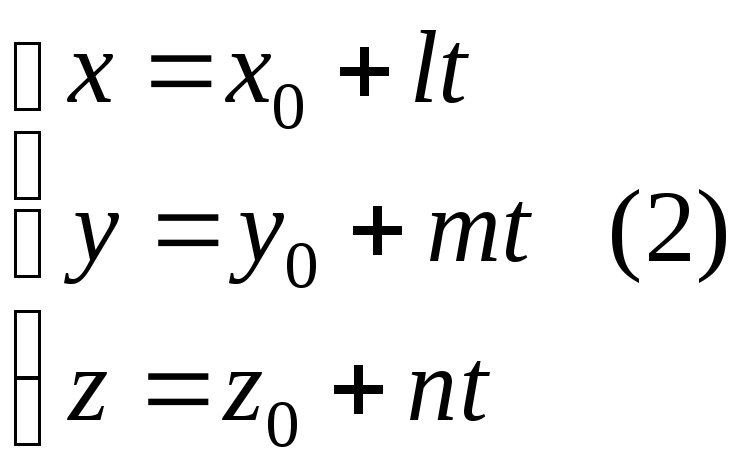 –параметричні
рівняння прямої в просторі.
–параметричні
рівняння прямої в просторі.
![]() – параметр.
– параметр.
З
(1) дістаємо:
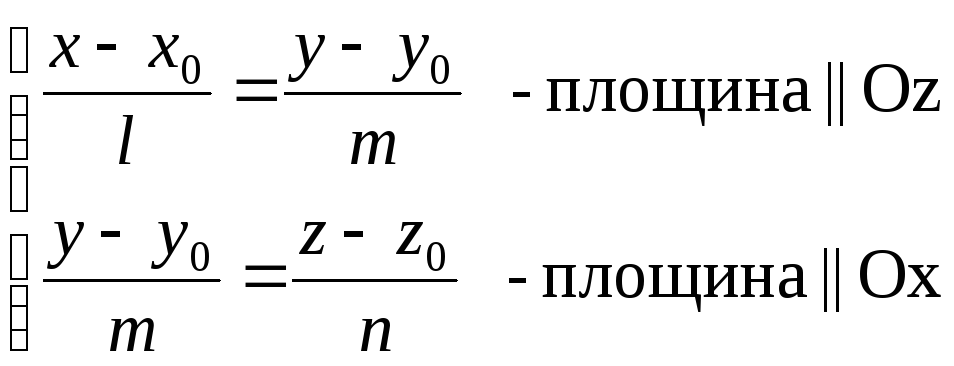
Канонічне рівняння задає пряму, як перетин трьох площин, кожна з яких паралельна координатній осі.
![]() –р-ня
прямої, що проходить ч/з дві точки в
просторі.
–р-ня
прямої, що проходить ч/з дві точки в
просторі.
Дві прямі в просторі Задані дві прямі:
![]()
![]() ;
;
![]()
![]()
Умова
паралельності:
![]()
![]() (1’)
(1’)
Якщо крім (1’) виконується також рівність (2’), то прямі співпадають:
![]()
![]()
Умова
перетину прямих:
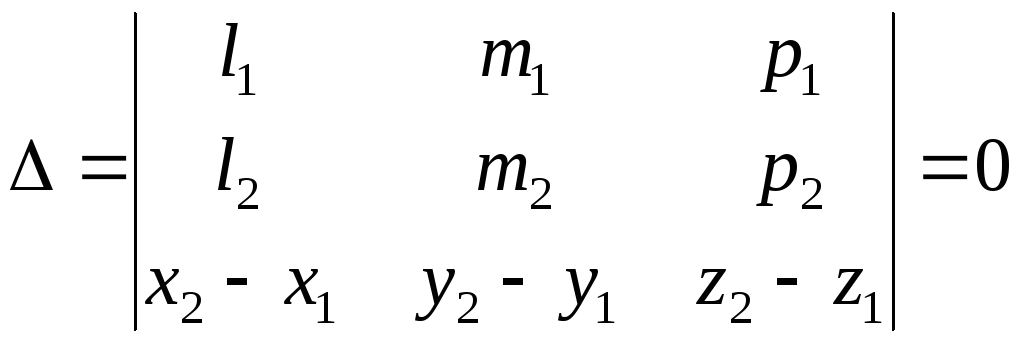 .
.
Умова
мимобіжності прямих:
![]()
Кут
між прямими рахують як кут між напрямними
векторами .
.
Кут між двома мимобіжними – це кут між паралельними до них прямими.
Площина в
просторі ![]()
![]()
![]() ;
;![]() ;
;![]() n–пер-р
до пл.
n–пер-р
до пл.
Дві площини в
просторі ![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
(![]() *)-
умова паралельності, якщо вона не
виконується, то площини перетинаються;
*)-
умова паралельності, якщо вона не
виконується, то площини перетинаються;
умова спів падання
Кут
між площинами:
![]() =
=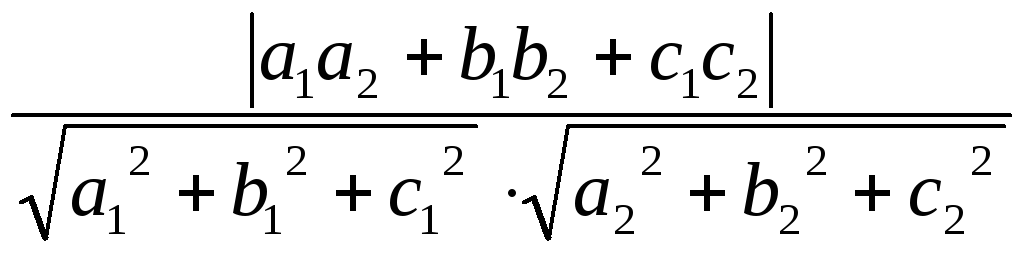
![]() =0
– площини перпендикулярні
=0
– площини перпендикулярні
Пряма і площина в просторі
![]()
![]()
![]()
![]()
![]() d;
d;
![]()
2)
![]()
2’)
якщо крім цього
![]()
![]()
1)
![]()
1’)
![]() –
колінеарні.
–
колінеарні.
![]() .
.
![]() –кут
між прямою і площиною.
–кут
між прямою і площиною.
2. Основні алгебраїчні структури: група, кільце, поле.
а)Група
Непорожня
множина із визначеною в ній бінарною
операцією
![]() ,
називаєтьсягрупоїдом.
Групоїд, в якому визначена асоціативна
операція, називається півгрупою.
Півгрупа, в якій існує одиничний
(нейтральний) елемент, називається
моноїдом.
Одиничний елемент позначають е:
для будь-якого g
,
називаєтьсягрупоїдом.
Групоїд, в якому визначена асоціативна
операція, називається півгрупою.
Півгрупа, в якій існує одиничний
(нейтральний) елемент, називається
моноїдом.
Одиничний елемент позначають е:
для будь-якого g![]() G
[g
G
[g![]() e
= e
e
= e![]() g
= g].
Моноїд, кожен елемент якого оборотний,
називається групою.
Оборотним називається
такий елемент множини, для якого в цій
множині існує обернений. Оберненим
до елемента
g
g
= g].
Моноїд, кожен елемент якого оборотний,
називається групою.
Оборотним називається
такий елемент множини, для якого в цій
множині існує обернений. Оберненим
до елемента
g![]() G
називається такий елемент g-1
цієї ж множини, для якого g
G
називається такий елемент g-1
цієї ж множини, для якого g![]() g-1=
g-1
g-1=
g-1![]() g
= e.
g
= e.
Повне
означення групи:
Непорожня множина G,
на якій визначено бінарну операцію
![]() , називаєтьсягрупою,
якщо
виконуються наступні умови:
, називаєтьсягрупою,
якщо
виконуються наступні умови:
операція
 асоціативна;
асоціативна;в множині G існує одиничний елемент ;
кожний елемент g
 G
множиниG
оборотний.
G
множиниG
оборотний.
Якщо
операція
![]() , визначена в групі, є комутативною, то
групаG
називається комутативною
або абелевою.
, визначена в групі, є комутативною, то
групаG
називається комутативною
або абелевою.
Група G називається скінченною, якщо кількість її елементів (порядок групи) скінченна.
Непорожню підмножину h групи g називають підгрупою цієї групи, якщо н є групою відносно бінарної операції, визначеної в групі g.
Перевірка того, чи непорожня підмін-на Н групи G є підг-ю групи G, включає:
чи містить Н разом із будь-якими своїми елементами g1 та g2 і результат операції між ними, тобто елемент g1
 g2;
g2;чи містить Н разом із будь-яким своїм елем-м g і обернений йому еле-т g-1.
Т(про
перетин підгруп).Якщо
Н1
і Н2
– підгрупи групи G,
то їх перетин Н1![]() Н2
теж є підгрупою групи G.
Н2
теж є підгрупою групи G.
Д.
Якщо елементи a
i
b
належать перетину Н1![]() Н2,
то вони
містяться в кожній з підгруп Н1
та
Н2,
тому елементи ab
та a-1
теж містяться
в кожній з підгруп, а тому і в їх перетині.
Отже, Н1
Н2,
то вони
містяться в кожній з підгруп Н1
та
Н2,
тому елементи ab
та a-1
теж містяться
в кожній з підгруп, а тому і в їх перетині.
Отже, Н1![]() Н2
– теж
підгрупа групи G.▲
Н2
– теж
підгрупа групи G.▲
Підгрупа,
що складається з усіх степенів елемента
g![]() G,
називається циклічною
підгрупою групи G,
породженою елементом g.
Позначається <g>.
G,
називається циклічною
підгрупою групи G,
породженою елементом g.
Позначається <g>.
Група G називається циклічною, якщо вона складається тільки зі степенів одного із своїх елементів g, тобто збігається з однією із своїх циклічних підгруп <g>. Елемент g називають твірним елементом циклічної групи <g>. Кожна циклічна група є абелевою.
Групи
G
i
G1
називаються
ізоморфними,
якщо між їх елементами можна встановити
таку взаємно однозначну відпов-ть, що
коли будь-яким елементам a,b![]() G
відповідають елементи a1,b1
G
відповідають елементи a1,b1![]() G1,
то результату операції a
G1,
то результату операції a![]() b
між елементами групи G
відповідає результат операції a1
b
між елементами групи G
відповідає результат операції a1![]() b1
між елем-ми групи G1.
b1
між елем-ми групи G1.
Тут
![]() – позначення операції в групіG,
– позначення операції в групіG,
![]() – в групіG1.
– в групіG1.
При ізоморфному відображенні груп G та G1:
одиничний елемент групи G відображається в одиничний елемент групи G1;
будь-яка пара взаємнообернених елементів g та g-1 групи G відображається в пару взаємнообернених елементів групи G1.
Кільце Непорожня множина К, на якій визначено операції додавання і множення, називається кільцем, якщо виконуються такі умови:
множина К є адитивною абелевою групою;
множина К є мультиплікативною півгрупою;
операція множення дистрибутивна відносно додавання, тобто
![]() a,b,cєK
[(a+b)c
=
ac+bc;
c(a+b)
=
ca+cb].
Позначається (К,+, •).
a,b,cєK
[(a+b)c
=
ac+bc;
c(a+b)
=
ca+cb].
Позначається (К,+, •).
Кільце наз-ть комутативним, якщо операція множення в кільці комут-на.
Ненульове кільце, в якому є один-й ел-т е, наз-ть кільцем з одиницею.
Елементи
а,b
кільця К називаються дільниками
нуля, якщо
а![]() θ,b
θ,b![]() θ,
але ab
= θ. θ
– нульовий елемент кільця.
θ,
але ab
= θ. θ
– нульовий елемент кільця.
Комутативне кільце з одиницею, в якому немає дільників нуля, називається цілісним кільцем (областю цілісності).
Підмножина К1 кільця К називається підкільцем кільця К, якщо К1 є кільцем відносно операцій додавання і множення, визначених в кільці К.
Перевірка того, що дана підмножина кільця є його підкільцем, включає вияснення, чи різниця й добуток довільних двох елементів підмножини К1 належить до К1.
Кільця
К і К1
називаються ізоморфними,
якщо між їх елементами можна встановити
таку взаємно однозначну відповідність,
що для будь-яких елементів a,b![]() К
і відповідних їм елементів a1,b1
К
і відповідних їм елементів a1,b1![]() К1
сумі a+b
відповідає сума a1+b1,
добутку ab
відповідає добуток a1b1.
К1
сумі a+b
відповідає сума a1+b1,
добутку ab
відповідає добуток a1b1.
Поле Комутативне кільце з одиницею, в якому кожен ненульовий елемент є оборотним, називається полем. Позначають (Р,+, •).
Поле (Р,+, •) являє собою поєднання в тій самій множині Р двох абелевих груп – адитивної (Р,+) та мультиплікативної (Р\{0},•).
Характеристикою поля Р називають:
число нуль, якщо ne=θ лише при n=0;
нат-не число р, якщо pe = θ і немає такого кєN, меншого ніж р, що ке= θ.
Підмножину Р1 поля Р називають підполем цього поля, якщо вона сама є полем відносно бінарних операцій, визначених у полі Р. Поле Р при цьому називають розширенням поля Р1.
