4. Факторний аналіз.

Факторний аналіз (факторний експеримент). Теоретичні основи закладені англійським математиком Р.Фішером в кінці 20-х років. Результати такого експерименту обробляють за деяким оптимальним алгоритмом з метою складання математичної моделі процесу у вигляді лінійного полінома. Суть факторного експерименту полягає в одночасному варіюванні всіх параметрів (факторів) за деяким планом, причому значення параметрів (факторів) встановлюють тільки в декількох точках допустимої області їх зміни і позначають символами (кодами) +1 (верхній рівень), -1 (нижній рівень) та 0 (середній рівень). План зміни значень факторів складає так звану матрицю планування.

Повним факторним експериментом (ПФЕ) називається такий, в якому реалізуються всі можливі комбінації (набори) рівнів факторів. Якщо n факторів варіюються на двох рівнях, то кількість всіх можливих наборів – N₂ = 2ⁿ (такий екперимент називають ПФЕ типу 2ⁿ), якщо на трьох рівнях, то N₃ = 3ⁿ (такий експеримент називають ПФЕ типу Зⁿ).

Кодування здійснюється за очевидним співвідношенням

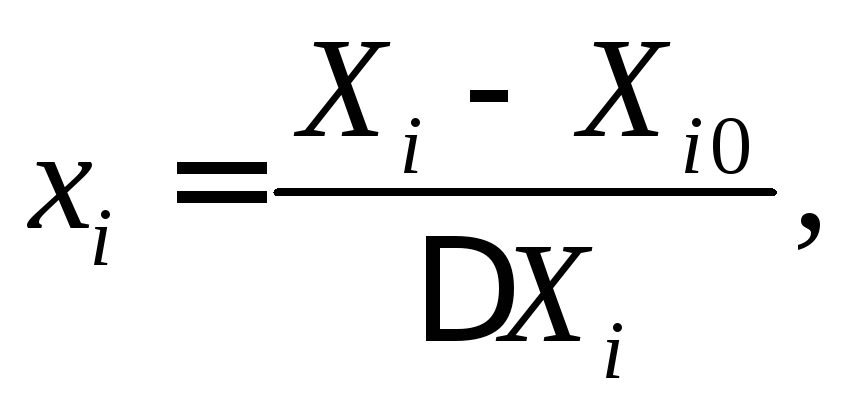де х_і - кодоване значення і - го фактора на верхньому або нижньому рівні, X_i0 - нульовий рівень натуральної (фізичної) змінної, X_i - верхній або нижній рівень натуральної змінної, ΔX_i - інтервал варіювання натуральної змінної відносно нульового рівня. Наприклад, при оцінці властивостей плоских оптичних фільтрів необхідно встановити залежність між довжиною хвилі λ, товщиною δ пластини фільтра та відносним пропусканням фільтра Α, тобто A=f(λ,δ) в діапазоні частот з довжиною хвилі λ = 600 - 700нм, δ = 1 - 2мм. Визначимо спочатку нульовий рівень факторів

λ₀=650 нм, δ=1,5 мм.

Тоді всі можливі комбінації факторів при варіюванні на двох рівнях (мінімальному та максимальному) будуть визначені чотирма дослідами, а на трьох рівнях необхідні 8 дослідів.

Результати експериментального дослідження для ПФЕ занесемо в таблицю.

Таблиця Матриця планування ПФЕ тину 2

N досліду	Рівні факторів		Вихідний параметр А, %
	λ |	δ
1	+1	+1	90
2	-1	+1	4
3	+1	-1	100
4	-1	-1	10

В кожній точці проводять декілька дослідів, які називаються паралельними, а значення вихідного параметра одержують усередненням всіх його значень в кожній з точок. Кількість паралельних дослідів встановлюють, як правило, рівним 2  4.

Розглянемо тепер особливості складання моделі на основі даних ПФЕ (спочатку на прикладі ПФЕ типу 2²).

Рівняння простої двофакторної моделі спочатку подамо так:

y = a₁ x₁ + a₂ x₂

Але в такому вигляді модель не відображає постійної складової рівняння, тому вводять поняття фіктивної змінної х₀ (тотожно рівної +1), а в матриці планування рівні змінних подамо відповідно + та - замість +1 та -1.

Таблиця Матриця ПФЕ типу 2² з фіктивною змінною

N досліду	Рівні факторії			Вихідний параметр
	x0 хо	x1	х2
1	+	+	+	y1
2	+	-	+	y2
3	+	+	-	y3
4	+	-	-	y4

Тоді, з врахуванням фіктивної змінної, лінійну модель для двох факторів подамо так:

y = a₀ x₀ + a₁ x₁ + a₂ x₂

Скористаємось методом найменших квадратів для визначення a₀, a₁, a₂.

_,Проаналізуємо коефіцієнти при a₀, a₁,та a₂. цієї системи. Виходячи з матриці планування ПФЕ типу 2², бачимо, що XXX завжди дорівнює кількості дослідів - 4, тобто

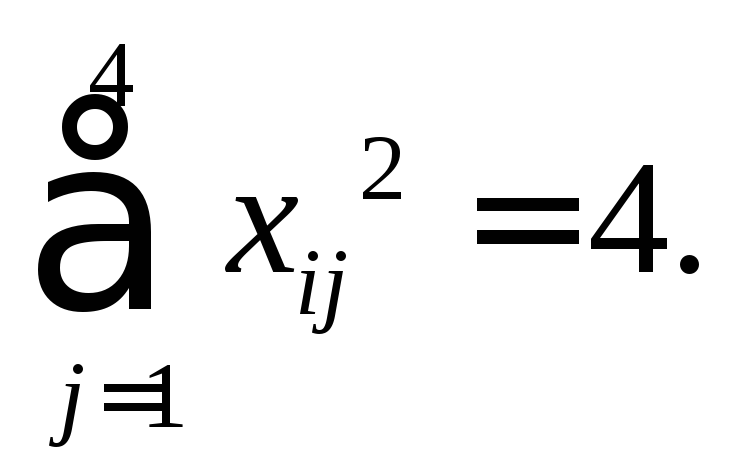Ця властивість називається властивістю нормування. Аналогічно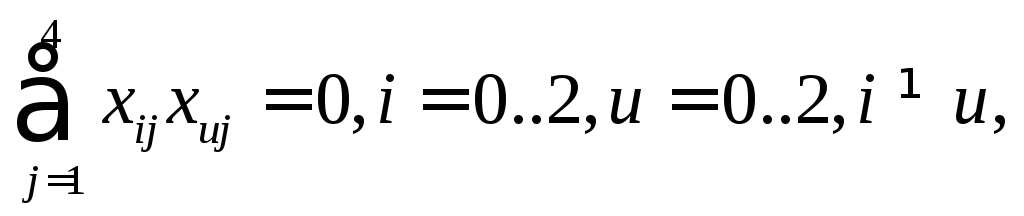

де i та u номер фактора.Ця властивість називається властивістю ортогональності.

В теорії планування експерименту показано, що цими властивостями володіють будь-які матриці ПФЕ типу 2².

Застосовуючи наведені властивості зобразимо систему у вигляді

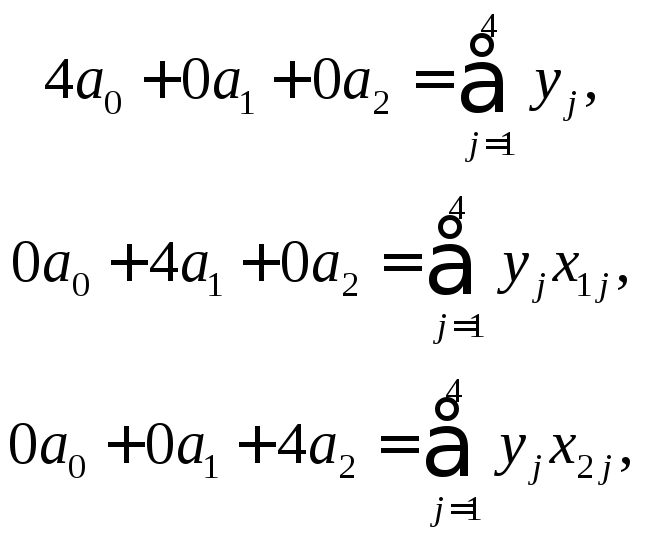коефіцієнтів регресії

або в загальному вигляді

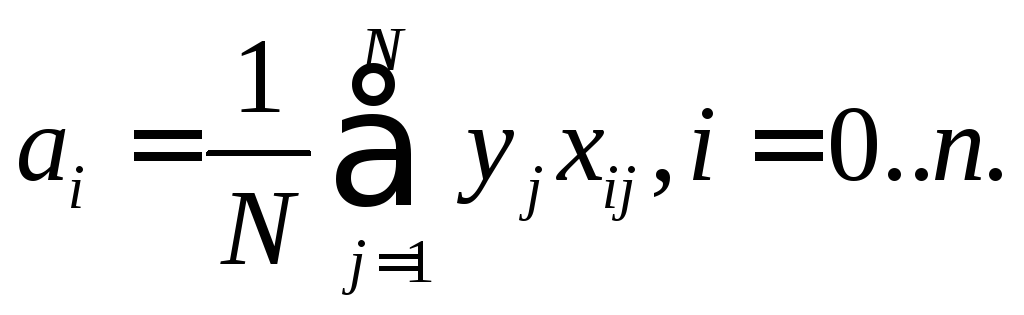Отже, а₀ - коефіцієнт регресії, що за змістом відповідає усередненому значенню вихідного параметра.