
1. Кореляційний аналіз. Характеристики парного та множинного статистичного зв'язку кількісних даних.
Матриця даних
Довільні об'єкти
дослідження характеризуються набором
параметрів, і за результатами спостереження
за їх функціонуванням формуються
багатовимірні сукупності (матриці)
експериментальних даних (ЕД) Величини,
що характеризують різні властивості
об'єктів, можуть бути незалежними або
взаємозв'язаними. Розрізняють два види
залежностей між величинами (чинниками):
функціональну і статистичну.
Величини,
що характеризують різні властивості
об'єктів, можуть бути незалежними або
взаємозв'язаними. Розрізняють два види
залежностей між величинами (чинниками):
функціональну і статистичну.
Рядки такої матриці відповідають результатам реєстрації всіх спостережуваних параметрів об'єкта в одному експерименті, а стовпці містять результати спостережень за одним параметром (фактором, варіантою) у всіх експериментах. Позначимо кількість параметрів через m (m>1), а кількість спостережень – через n.У матриці елемент хij відповідає значенню j-й варіанти в i-м спостереженні. Матриця може містити порожні значення деяких елементів, наприклад, через пропуски в реєстрації значень параметрів. У багатовимірному аналізі бажано усунути пропущені значення. Для цього існують спеціальні прийоми, зокрема, викреслювання відповідних рядків матриці або занесення середніх значень замість відсутніх. Надалі вважатимемо, що матриця не містить порожніх елементів, а параметри об'єкту характеризуються безперервними випадковими величинами.
Перехід від початкової до стандартизованої матриці здійснюється таким чином.
1.
За кожною із варіант j=1, 2 ..., m обчислюються
мат. очікування:
![]() і дисперсію
і дисперсію![]()
2.
Обчислюються елементи стандартизованої
матриці
![]() .Елементи
матриці U є безрозмірними величинами.
Саме матриця U буде об'єктом подальшої
обробки.Важливішим частным випадком
статистичної залежності є кореляційна
залежність, що характеризує взаємозв'язок
значень одних випадкових величин з
середнім значенням інших, хоча у кожному
окремому випадку будь-яка взаємозв'язана
величина може набувати різних значень.
.Елементи
матриці U є безрозмірними величинами.
Саме матриця U буде об'єктом подальшої
обробки.Важливішим частным випадком
статистичної залежності є кореляційна
залежність, що характеризує взаємозв'язок
значень одних випадкових величин з
середнім значенням інших, хоча у кожному
окремому випадку будь-яка взаємозв'язана
величина може набувати різних значень.
Якщо ж у взаємозв'язаних величин варіацію має лише одна змінна, а інша є детермінованою, то такий зв'язок називають не кореляційним, а регресійним. Наприклад, при аналізі швидкості обміну з жорсткими дисками можна оцінювати регресію цієї характеристики на певні моделі, але не слід говорити про кореляцію між моделлю і швидкістю.
Кореляційна залежність визначається різними параметрами, серед яких найбільшого поширення набули показники, що характеризують взаємозв'язок двох випадкових величин (парні показники): кореляційний момент, коефіцієнт кореляції.
Оцінка кореляційного моменту ( коефіцієнта коваріації ) два варіант xj і xk обчислюється по вихідній матриці Х
![]()
Цей показник незручний для практичного вживання, оскільки має розмірність, рівну добутку розмірності варіант, і по його величині важко судити про залежність параметрів.
Коефіцієнт коваріації rjk нормованих випадкових величин називають коефіцієнтом кореляції, його оцінка
![]() ,Коефіцієнт
кореляції залежить не від значень
випадкових величин, а від їх варіацій,
так якщо значення величини збільшити
на порядок, то коефіцієнт не зміниться.
Значення коефіцієнта кореляції лежить
в межах від – 1 до +1.В цілому інтерпретація
коефіцієнта кореляції полягає в
наступному: відхилення однієї випадкової
величини від середнього значення на
величину середнього квадратичного
відхилення наводить в середньому по
сукупності до відхилення іншої випадкової
величини від свого середнього значення
на величину її середнього квадратичного
відхилення.Оцінка коефіцієнта кореляції,
обчислена по обмеженій вибірці, практично
завжди відрізняється від нуля.Використовуючи
поняття коефіцієнта кореляції, матриці
ЕД можна поставити у відповідність
квадратну матрицю оцінок коефіцієнтів
кореляції (кореляційну матрицю)
,Коефіцієнт
кореляції залежить не від значень
випадкових величин, а від їх варіацій,
так якщо значення величини збільшити
на порядок, то коефіцієнт не зміниться.
Значення коефіцієнта кореляції лежить
в межах від – 1 до +1.В цілому інтерпретація
коефіцієнта кореляції полягає в
наступному: відхилення однієї випадкової
величини від середнього значення на
величину середнього квадратичного
відхилення наводить в середньому по
сукупності до відхилення іншої випадкової
величини від свого середнього значення
на величину її середнього квадратичного
відхилення.Оцінка коефіцієнта кореляції,
обчислена по обмеженій вибірці, практично
завжди відрізняється від нуля.Використовуючи
поняття коефіцієнта кореляції, матриці
ЕД можна поставити у відповідність
квадратну матрицю оцінок коефіцієнтів
кореляції (кореляційну матрицю)
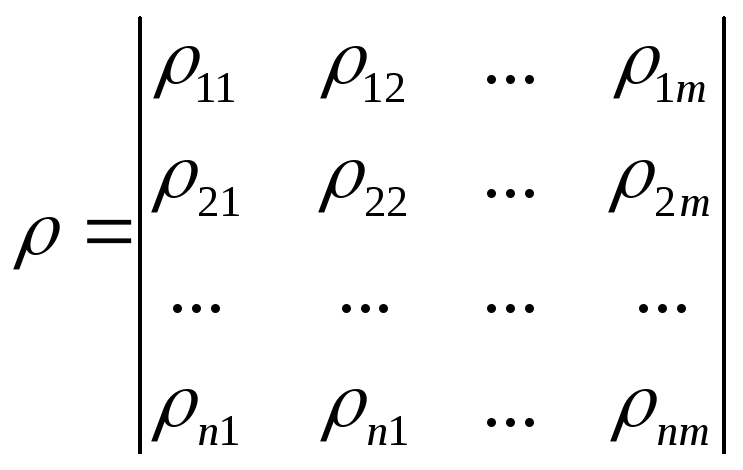 Діагональні
елементи матриці = 1, а симетричні відносно
діагоналі рівні між собою.
Діагональні
елементи матриці = 1, а симетричні відносно
діагоналі рівні між собою.
Перевірка гіпотези про значущість оцінки коефіцієнта кореляції вимагає знання розподілу цієї випадкової величини. Розподіл величини ik вивчено лише для окремого випадку, коли випадкові величини Uj и Uk розподілені по нормальному закону.
Як
критерій перевірки нульової гіпотези
Н0
застосовують випадкову величину
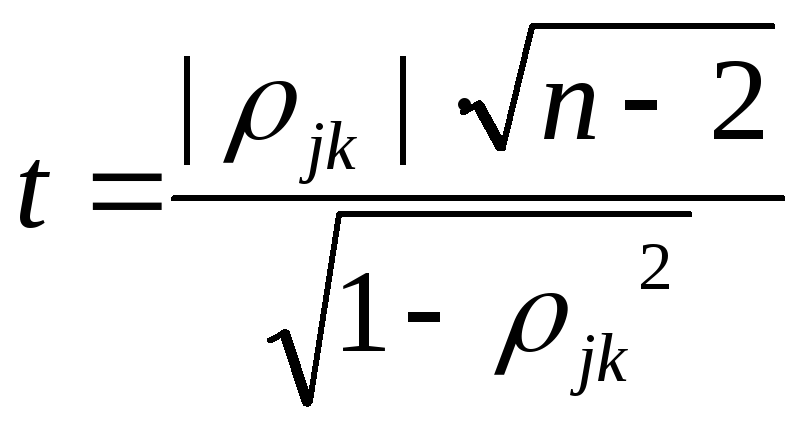 .Якщо
модуль коефіцієнта кореляції відносно
далекий від одиниці, то величина t при
справедливості нульової гіпотези
розподілена згідно із законом Стьюдента
з n–2 мірами свободи. Конкуруюча гіпотеза
Н1
відповідає твердженню, що значення ik
не
дорівнює нулю (більше або менше нуля).
Тому критична область двостороння.
Перевірка гіпотези Н0
про рівність нулю генерального коефіцієнта
парної кореляції двовимірної нормально
розподіленої випадкової величини
здійснюється в наступній послідовності:
.Якщо
модуль коефіцієнта кореляції відносно
далекий від одиниці, то величина t при
справедливості нульової гіпотези
розподілена згідно із законом Стьюдента
з n–2 мірами свободи. Конкуруюча гіпотеза
Н1
відповідає твердженню, що значення ik
не
дорівнює нулю (більше або менше нуля).
Тому критична область двостороння.
Перевірка гіпотези Н0
про рівність нулю генерального коефіцієнта
парної кореляції двовимірної нормально
розподіленої випадкової величини
здійснюється в наступній послідовності:
1. обчислюється значення статистики t;
2. при рівні значущості для двосторонньої області визначається критична точка розподілу Стьюдента tкр(n–2; ), таблиця. П.4;
3. порівнюється значення статистики t з критичним значенням tкр(n–2; ). Якщо
t< tкр(n–2; ),
то немає підстав відкинути нульову гіпотезу, інакше гіпотеза Н0 відкидається (коефіцієнт кореляції значимий).
