ТЕСТИ_ЗНО_МАТЕМ

35.43.З точки А, що розміщена на колі, радіус якого дорівнює 2, побудований перпендикуляр AK завдовжки 1 до площини круга. З точки А проведено діаметр АВ, а з точки В під кутом 45° до діаметра — хорду ВС. Знайти у сантиметрах відстань від точки K до хорди ВС.

35.44.Основи трапеції дорівнюють 18 см і 12 см. Через більшу основу проведено площину на відстані 5 см від меншої основи. Знайти у сантиметрах відстань від точки перетину діагоналей трапеції до цієї площини.

35.45.З точок А і В, які лежать у двох перпендикулярних площинах, опущено перпендикуляри АА1 і

ВВ1 на лінію перетину площин. Знайти АВ, якщо АВ1 = 7, ВА1 = 5, A1B1 = 10 .

35.46. Рівнобедрені трикутники АВС і АВD зі спільною основою АВ лежать у різних площинах, кут між якими дорівнює α. Знайти у градусах кут α, якщо АВ = 6, СD = 21 , АС = АD = 4.

35.47. Дано куб АВСDА1В1С1D1. Знайти площу перерізу куба площиною, яка проходить через верши-

35.49.Дано куб АВСDА1В1С1D1 Знайти площу перерізу куба з точністю до 0,01 площиною, яка проходить через центр куба і середини ребер АВ і АD, якщо ребро куба дорівнює 1.

35.50.Через центр основи правильної трикутної піраміди паралельно до двох ребер, які не перетинаються, проведено площину. Визначити площу утвореного перерізу, якщо бічне ребро піраміди дорівнює 9, а ребро основи — 7.

35.51.У правильній чотирикутній піраміді проведено площину через діагональ основи паралельно до

бічного ребра. Сторона основи дорівнює 2 , а бічне ребро — 5. Визначити площу утвореного перерізу.

35.52.У правильній чотирикутній піраміді SABCD через середини сторін АВ і АD проведено площину, яка паралельна бічному ребру SA. Знайти площу утвореного перерізу, якщо сторона основи дорівнює 2 , а бічне ребро — 5.

35.53.Площина трикутника АВС, сторони якого дорівнюють 18 см, 20 см і 34 см, паралельна до пло-

щини α. Світло, що виходить з точки S, утворює на площині α тінь А1В1С1 від трикутника АВС. Обчислити у квадратних сантиметрах площу тіні, якщо SA : A1A = 5 : 3.

261

ТЕМА 36. ПРИЗМА

Завдання 36.1–36.30 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.

36.1.Сторона куба дорівнює 10 см. Знайти площу поверхні куба.

36.2.Діагональ грані куба дорівнює 4 2 см. Знайти об’єм куба.

36.3.Обчислити довжину ребра куба, діагональ якого дорівнює 2 3 .

36.4.Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 6 см.

36.5.Сторони основи прямокутного паралелепіпеда дорівнюють 5 см і 12 см, а діагональ паралелепіпеда нахилена до площини основи під кутом 45°. Знайти бічне ребро паралелепіпеда.

36.6.У правильній трикутній призмі радіус кола, вписаного в основу, дорівнює 2 3 см. Діагональ бічної грані утворює з площиною основи кут 45°. Обчислити площу бічної поверхні призми.

36.7. Основою прямої призми є прямокутний трикутник з гіпотенузою 10 см і катетом 6 см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5 см.

36.8. Площа бічної грані правильної трикутної призми дорівнює 96 см2, а периметр основи — 12 см. Обчислити бічне ребро призми.

36.10.У правильній трикутній призмі діагональ бічної грані дорівнює 5 см. Обчислити висоту призми, якщо висота основи дорівнює 2 3 см.

262

36.11.Сторона основи правильної трикутної призми дорівнює 4 см, а бічне ребро дорівнює 2 3 см. Знайти об’єм призми.

36.12.В основі прямої призми лежить ромб зі стороною 5 см і діагоналлю 8 см. Обчислити об’єм призми, якщо діагональ бічної грані дорівнює 13 см.

36.13.Сторона основи правильної трикутної призми дорівнює 12 см, а діагональ бічної грані дорівнює 13 см. Знайти бічну поверхню призми.

36.14. В основі прямої призми лежить прямокутний трикутник з катетами 8 см і 6 см. Діагональ бічної грані, що містить гіпотенузу цього трикутника, дорівнює 26 см. Обчислити площу бічної поверхні призми.

36.15. Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює а, а висота — Н.

36.16.В основі прямої призми лежить рівнобічна трапеція з основами 4 см і 10 см і бічною стороною 5 см. Бічне ребро призми дорівнює 10 см. Обчислити повну поверхню призми.

36.17.В основі прямої призми лежить прямокутна трапеція з основами 9 см і 14 см і більшою бічною стороною 13 см. Обчислити об’єм призми, якщо менша її діагональ дорівнює 25 см.

36.18.Основою похилої призми є паралелограм зі сторонами 6 см і 3 см і гострим кутом 45°. Бічне ребро призми дорівнює 4 см і нахилене до площини основи під кутом 30°. Знайти об’єм призми.

36.19.Бічне ребро похилої чотирикутної призми дорівнює 12 см, а перпендикулярним перерізом є ромб зі стороною 5 см. Знайти площу бічної поверхні призми.

36.20.Куб з ребром 1 м поділили на кубики з ребром 1 см й усі ці кубики поставили в стовпець. Чому дорівнює висота стовпця?

263

36.21. Площа діагонального перерізу куба дорівнює 4 2 см2. Знайти площу поверхні куба.

36.22.Основою прямого паралелепіпеда є ромб. Площі його діагональних перерізів дорівнюють S1 і S2. Визначити висоту паралелепіпеда, якщо його об’єм дорівнює V.

36.23.Діагональ правильної чотирикутної призми дорівнює 13 см, а діагональ бічної грані дорівнює 12 см. Знайти площу основи призми.

36.24.У правильній чотирикутній призмі площа діагонального перерізу дорівнює S. Визначити площу бічної поверхні.

36.25.Діагональним перерізом правильної чотирикутної призми є квадрат, площа якого дорівнює S. Визначити об’єм призми.

36.26.Основою прямого паралелепіпеда є ромб, площа якого дорівнює S, а площі діагональних перерізів паралелепіпеда — S1 і S2. Визначити висоту паралелепіпеда.

36.27.Бічна поверхня правильної чотирикутної призми дорівнює 32 м2, а повна її поверхня — 40 м2. Знайти висоту призми.

36.28.Бічна поверхня правильної чотирикутної призми дорівнює Q, а її об’єм — V. Визначити сторону основи призми.

36.29.Розгорткою бічної поверхні правильної чотирикутної призми є квадрат зі стороною 8 дм. Знайти об’єм призми.

264

36.30.Площі трьох граней прямокутного паралелепіпеда дорівнюють S1, S2 і S3. Визначити об’єм паралелепіпеда.

Завдання 36.31–36.34 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).

36.31.Установити відповідність між сторонами основи та діагоналями (1–4) бічних граней правильних трикутних призм та площами їх бічних поверхонь (А–Д).

36.32.Основою прямої призми є рівнобедрений трикутник, бічна сторона якого дорівнює 10 см, а кут при основі дорівнює arcsin0,8. Бічне ребро призми дорівнює 4 см. Установити відповідність між площами фігур (1–4) та їх числовими значеннями (А–Д).

36.33.Установити відповідність між площами діагональних перерізів (1–4), які є квадратами у правильних чотирикутних призм, та об’ємами цих призм (А–Д).

36.34. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).

4У куб вписано кулю, діаметр якої дорівнює 2. Обчислити площу повної поверхні куба

265

Розв’яжіть завдання 36.35–36.53. Відповідь запишіть десятковим дробом.

36.35.Сторона основи правильної трикутної призми дорівнює 12, а висота призми — 6. Знайти площу перерізу цієї призми площиною, яка проходить через сторону нижньої основи і протилежну вершину.

36.36.Діагональ правильної чотирикутної призми утворює з площиною основи кут 45°. Знайти у градусах кут, утворений цією діагоналлю з площиною бічної грані.

36.37.Основою паралелепіпеда є ромб. Діагоналі паралелепіпеда дорівнюють 8 см і 5 см, а висота — 2 см. Знайти у сантиметрах сторону основи.

36.38.Діагоналі граней прямокутного паралелепіпеда мають довжини 2, 2 i 2 6 . Визначити діагональ паралелепіпеда.

36.39.Визначити об’єм прямокутного паралелепіпеда, основою якого є прямокутник зі сторонами 3 і 4, а площа діагонального перерізу 20.

36.40.У прямому паралелепіпеді сторони основи 2 і 8, а кут між ними 30°. Бічна поверхня паралелепіпеда дорівнює 20. Визначити об’єм паралелепіпеда.

36.41.Периметри двох граней правильної трикутної призми дорівнюють 48 см і 30 см. Знайти об’єм

V призми у кубічних сантиметрах. У відповідь записати V .

3

36.42. Основа призми — правильний трикутник АВС зі стороною 6 см. Вершина призми А1 проектується в центр нижньої основи, а ребро АА1 нахилено до площини основи під кутом 60°. Визна-

чити площу бічної поверхні Sб.. У відповідь записати ( 39 − 12)Sб..

36.43.У похилій трикутній призмі відстані між бічними ребрами дорівнюють 37 см, 13 см і 40 см. Знайти відстань між бічною гранню з найбільшою площею і протилежним бічним ребром.

36.44.Знайти у кубічних сантиметрах об’єм похилої трикутної призми, якщо відстані між її бічними ребрами дорівнюють 3,7 см, 1,3 см і 3 см, а площа бічної поверхні — 480 см2.

36.45.У похилій трикутній призмі дві бічні грані рівні між собою, а кут між ними дорівнює 60°. Їх спільне ребро віддалене від протилежної бічної грані на відстань 3 дм. Довжина бічного ребра дорівнює 4 3 дм. Визначити об’єм призми.

36.46.Основою похилого паралелепіпеда є ромб зі стороною 4 см і гострим кутом 60°. Бічне ребро паралелепіпеда дорівнює 4 см й утворює з ребрами основи, які виходять з цієї ж вершини, кути 45°. Знайти об’єм паралелепіпеда у кубічних сантиметрах.

36.47.Площина, яка проходить через сторону основи правильної трикутної призми і середину протилежного ребра, утворює з основою кут 45°. Сторона основи дорівнює 2 см. Обчислити в кубічних сантиметрах об’єм призми.

36.48.Висота правильної чотирикутної призми дорівнює 5, а кут між діагоналями, проведеними з однієї вершини основи у двох суміжних бічних гранях, — 60°. Визначити площу бічної поверхні призми.

36.49.Основою похилої призми є правильний трикутник, сторона якого дорівнює 2 см. Довжина бічного ребра призми дорівнює 4 см, а одне з бічних ребер утворює з прилеглими ребрами кути по 45°. Обчислити в кубічних сантиметрах об’єм призми.

36.50.Основою призми є правильний трикутник зі стороною 4. Одна з бічних граней перпендикулярна до основи і є ромбом, діагональ якого дорівнює 6. Знайти об’єм V призми. У відповідь записати 21V .

36.51.Основою похилого паралелепіпеда є прямокутник зі сторонами 4 і 6. Бічне ребро дорівнює 2 й утворює із суміжними сторонами основи кути в 60°. Знайти об’єм V паралелепіпеда. У відпо-

відь записати 2V .

36.52.Для зберігання 1,8 м3 води на присадибній ділянці виготовили резервуар у формі прямокутного паралелепіпеда з квадратним дном, сторона якого дорівнює 1,2 м. Обчислити висоту резервуару.

36.53.Діаметр кулі, описаної навколо куба, дорівнює 3 3. Обчислити об’єм куба.

266

ТЕМА 37. ПІРАМІДА

Завдання 37.1–37.29 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.

37.1.Сторона основи правильної трикутної піраміди дорівнює b 3 , а висота піраміди — Н. Визначити бічне ребро піраміди.

37.2.Площа бічної поверхні правильної трикутної піраміди дорівнює 144 см2, а сторона основи — 4 см. Обчислити апофему піраміди.

37.3.Сторона основи правильної чотирикутної піраміди дорівнює а. Бічна грань нахилена до площини основи під кутом β. Визначити апофему піраміди.

37.4.Діагональний переріз правильної чотирикутної піраміди — правильний трикутник, площа якого дорівнює 9 3 см2. Обчислити площу основи піраміди.

37.5.Сторона основи правильної трикутної піраміди дорівнює 6 см, а бічне ребро — 5см. Знайти бічну поверхню піраміди.

37.6.Ребро куба ABCDA1B1C1D1 дорівнює 6 см. Знайти об’єм піраміди з основою BDD1 і вершиною С.

37.7.У скільки разів збільшиться об’єм чотирикутної піраміди, якщо кожну сторону її основи збільшити удвічі, а висоту збільшити у 6 разів?

37.8.Висота правильної чотирикутної піраміди дорівнює 8 см, апофема піраміди — 10 см. Знайти у квадратних сантиметрах площу перерізу піраміди, проведеного через середину висоти паралельно до площини основи.

37.9. Висота та бічне ребро правильної чотирикутної піраміди відповідно дорівнюють 3 см і 5см. Знайти об’єм піраміди.

267

37.10.Основою піраміди є трикутник зі сторонами 5 см, 12 см і 13 см. Знайти висоту піраміди, якщо бічні грані нахилені до площини основи під кутом 45°.

37.11.Основою піраміди є трикутник зі сторонами 6 см, 8 см і 10 см. Знайти висоту піраміди, якщо всі її бічні ребра рівні та дорівнюють 13 см.

37.12.Основа піраміди — квадрат зі стороною а. Висота піраміди дорівнює Н і проходить через одну з вершин основи. Визначити площу бічної поверхні піраміди.

37.13.Висота піраміди поділена на 4 рівні частини і через точки поділу проведено перерізи, паралельні до основи. Знайти площу найбільшого перерізу, якщо площа основи дорівнює 800 см2.

37.14.Знайти висоту правильної чотирикутної зрізаної піраміди, у якої сторони основ дорівнюють а і b (a > b), а кут нахилу бічного ребра до більшої основи дорівнює α.

37.15.У правильній зрізаній чотирикутній піраміді сторони основи а і b (a > b), двогранний кут при більшій основі — β. Знайти висоту піраміди.

37.17. У правильній чотирикутній піраміді довжина сторони основи дорівнює 6 см, а довжина бічного

37.18.У правильній трикутній піраміді бічне ребро нахилено до площини основи під кутом 60°. Під яким кутом нахилена до площини основи бічна грань?

37.19.У правильній чотирикутній піраміді двогранний кут при основі дорівнює 45°. Під яким кутом нахилено до площини основи бічне ребро?

268

37.20.Площа основи правильної трикутної піраміди дорівнює S, а площа бічної поверхні — Q. Визначити двогранний кут при основі.

37.22. Діагональним перерізом правильної чотирикутної піраміди є прямокутний трикутник, площа якого дорівнює Q. Знайти площу основи піраміди.

37.23.Сторона основи правильної трикутної піраміди дорівнює а, а площа перерізу піраміди площиною, яка проходить через бічне ребро і перпендикулярна до основи, дорівнює Q. Знайти об’єм піраміди.

37.25. В основі піраміди лежить прямокутний трикутник. Кожне бічне ребро піраміди дорівнює 5 5 см. Основа висоти піраміди віддалена від катетів цього трикутника на 3 см і 4 см. Обчислити об’єм піраміди.

37.26.Об’єм правильної чотирикутної піраміди дорівнює 512 см3, а висота піраміди — 6 см. Обчислити площу бічної поверхні піраміди.

37.27.В основі піраміди лежить прямокутний трикутник з катетом 10 см і протилежним до нього кутом 30°. Усі бічні ребрапірамідиутворюють з площиною основи кут60°. Знайтиоб’єм піраміди.

37.28.Бічні ребра трикутної піраміди попарно перпендикулярні й дорівнюють а, b і c. Визначити об’єм піраміди.

269

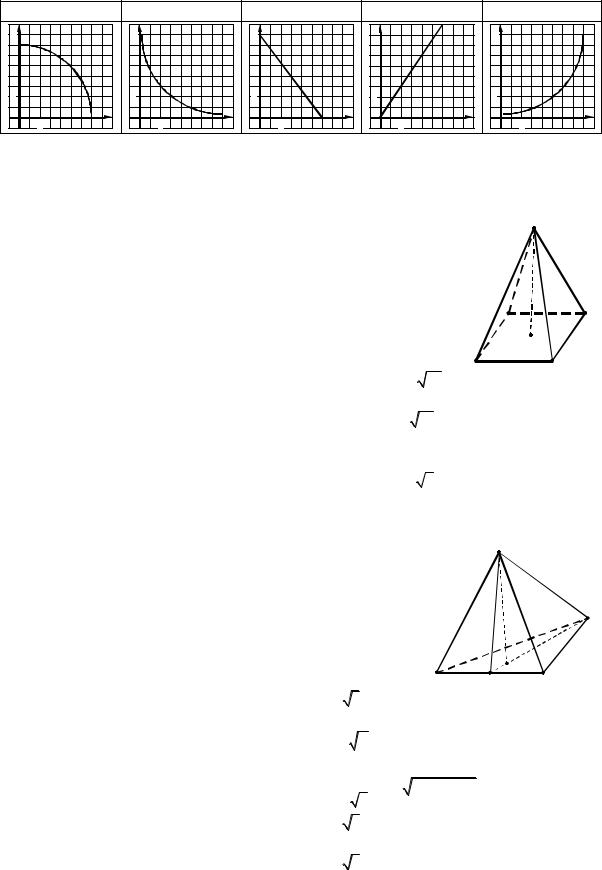
37.29.S(x) — площа перерізу правильної чотирикутної піраміди, проведеного паралельно до основи на відстані x від неї. Який з наведених графіків може бути графіком функції S(x)?

Завдання 37.30–37.36 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).

270