ТЕСТИ_ЗНО_МАТЕМ

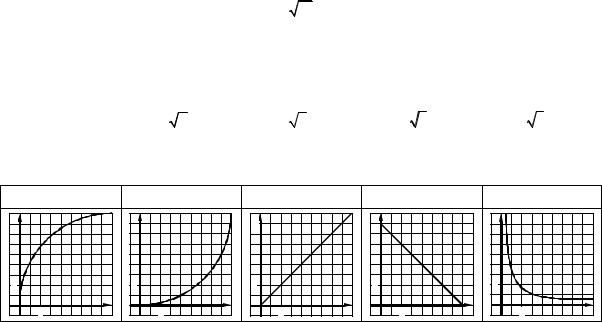
31.24.Знайти радіус кола, вписаного в рівнобедрений трикутник, основа якого дорівнює 160 см а висота, проведена до неї, — 60 см.

31.25. Знайти відстань від точки перетину медіан до центра кола, вписаного в рівнобедрений трикутник з основою 160 см і бічною стороною 100 см.

31.27.Основа і бічна сторона рівнобедреного трикутника відповідно дорівнюють 16 см і 10 см. Знайти висоту трикутника, проведену до бічної сторони.

31.28.Периметр рівнобедреного трикутника дорівнює 72 см. Бісектриса кута при основі ділить медіану, проведену до основи, на відрізки у відношенні 5 : 4. Знайти більшу сторону трикутника.

31.29.Медіана, проведена до бічної сторони рівнобедреного трикутника, утворює з основою кут 45°. Знайти тангенс кута при основі трикутника.

31.30.Бічна сторона рівнобедреного трикутника дорівнює 48 см. За якого значення висоти, проведеної до основи, площа трикутника буде найбільшою?

31.31.S — площа рівностороннього трикутника. Серед наведених графіків указати графік залежності периметра Р від S: Р = Р(S).

231

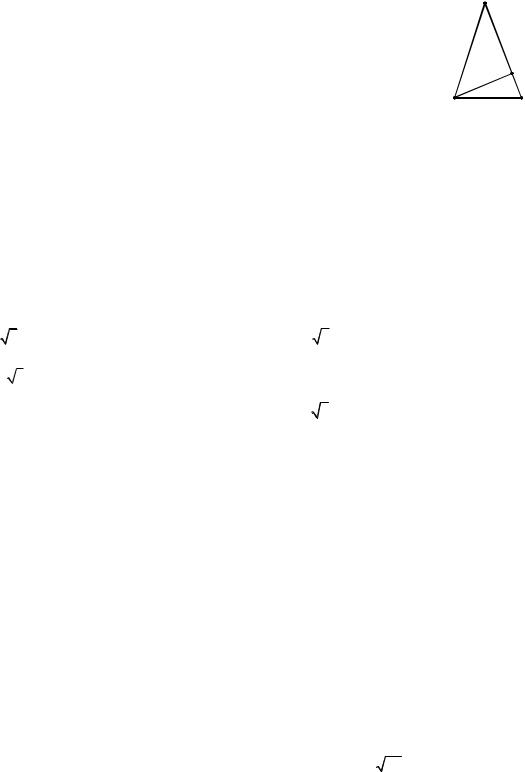
Завдання 31.32–31.38 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).

31.32.На рисунку зображено рівнобедрений трикутник ABC (AC = BC), його висоту AD і позначено величини деяких елементів. Установити відповідність між елементами трикутника (1–4) та їхніми величинами (А–Д).

31.33.У рівнобедреному трикутнику АВС з основою АС кут при вершині дорівнює 84°. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).

4Обчислити кут між висотою, проведеною до бічної сторони, та медіаною, проведеною до основи

31.34.Установити відповідність між заданими довжинами основ (1–4) рівнобедрених трикутників з кутами 120° при вершинах, протилежних до основ, та їх висотами (А–Д) до цих основ.

31.35.Установити відповідність між довжинами бічних сторін рівнобедрених трикутників (1–4), кут між якими дорівнює 30°, та площами (А–Д) цих трикутників.

31.36. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).

3Периметр рівнобедреного трикутника дорівнює 64 см, а бісектриса кута при вершині дорівнює 16 см. Обчислити площу цього трикутника

4У рівнобедреному трикутнику медіана, проведена до основи, дорівнює 24 см, а медіана, проведена до бічної сторони, — 3 97 см. Знайти площу трикутника

232

31.37.Установити відповідність між довжинами сторін рівнобедрених трикутників (1–4) та радіусами описаних навколо них кіл (А–Д).

31.38.Кут між бічними сторонами рівнобедреного трикутника дорівнює β, а основа трикутника — а. Установити відповідність між задачами (1–4) та формулами для відшукання відповідей до них

(А–Д).

Д a

2sin(β / 2)

Розв’яжіть завдання 31.39–31.59. Відповідь запишіть десятковим дробом.

31.39.Периметр рівнобедреного трикутника дорівнює 20. Знайти його основу, якщо вона на 2 більша від бічної сторони.

31.40.Зовнішній кут при вершині рівнобедреного трикутника дорівнює 110°. У відповідь записати в градусах кут при основі цього трикутника.

31.41.Усередині трикутника АВС до сторони ВС проведено пряму AD так, що утворився рівнобедрений трикутник ADC з основою АС. Знайти в сантиметрах довжину АС, якщо периметри трикутників АВС і ABD відповідно дорівнюють 42 см і 30 см.

31.42.Кут при основі АВ рівнобедреного трикутника дорівнює 30°. Висоти трикутника, проведені до бічних сторін, перетинаються в точці О. Знайти у градусах величину кута АОВ.

31.43.У рівнобедреному трикутнику АВС основа АС дорівнює 18. Через точку О — середину висоти ВD — проведено промені АО і СО, які перетинають бічні сторони в точках М і K. Знайти довжину відрізка МK.

31.44.У рівнобедреному трикутнику основа і бічна сторона відповідно дорівнюють 5 і 20. Знайти менший з відрізків, на які поділяє бічну сторону бісектриса кута при основі.

31.45.У рівнобедреному трикутнику АВС основа АС дорівнює 12 см, а висота BD — 8 см. Через точку D проведено відрізок DM (М ВС) паралельно до бічної сторони АВ. Знайти в сантиметрах довжину цього відрізка.

31.46.У рівнобедреному трикутнику центр вписаного кола ділить висоту, проведену до основи, у відношенні 12 : 5, а бічна сторона дорівнює 60. Знайти периметр трикутника.

31.47.Бісектриса, проведена до бічної сторони рівнобедреного трикутника, ділить її на відрізки 25 см і 30 см, починаючи від вершини, яка протилежна до основи трикутника. Знайти у сантиметрах периметр трикутника.

233

31.48.У рівнобедреному трикутнику бічна сторона ділиться точкою дотику вписаного в нього кола у відношенні 8 : 5, починаючи від вершини. Знайти в сантиметрах радіус вписаного кола, якщо висота трикутника, проведена до основи, дорівнює 36 см.

31.49.У рівнобедреному трикутнику АВС АВ = ВС = 25 см, BD = 20 см — висота. Знайти в квадратних сантиметрах площу трикутника MBK, де M і K — основи висот трикутника АВС, проведених до бічних сторін трикутника.

31.50.Периметр рівнобедреного трикутника дорівнює 108 см, а основа — 30. Знайти радіус вписаного кола.

31.51.Висота, проведена до бічної сторони рівнобедреного трикутника, дорівнює 24 см, а медіана, проведена до основи, — 20 см. Обчисліть у сантиметрах периметр трикутника.

31.52.Основа рівнобедреного трикутника дорівнює 12, а висота, що проведена до основи, — 8. Знайти радіус кола, вписаного в цей трикутник.

31.53.У рівнобедреному тупокутному трикутнику точка перетину серединних перпендикулярів віддалена від основи на 7 см. Знайти в сантиметрах периметр трикутника, якщо довжина описаного навколо нього кола дорівнює 50π см.

31.54.Основа рівнобедреного трикутника дорівнює а, радіус вписаного кола — r. Визначити бічну сторону трикутника й обчислити її значення, якщо а = 6, r = 2.

31.55.У рівнобедреному трикутнику основа дорівнює а, висота, що проведена до основи, — h. Ви-

значити відстань від середини основи до бічної сторони й обчислити її значення, якщо а = 3, h = 2.

31.56.Знайти у градусах кут між бічними сторонами рівнобедреного трикутника, якщо бісектриса кута при основі відтинає від нього трикутник подібний даному.

31.57.Знайти площу рівнобедреного трикутника з точністю до 0,01 см2, якщо висота, яка проведена до бічної сторони, дорівнює 12 см, а інша висота — 9 см.

31.58.Бічна сторона рівнобедреного трикутника дорівнює b, медіана, яка проведена до бічної сторони, дорівнює m. Визначити квадрат основи трикутника й обчислити його значення, якщо m = 2,5; b = 3.

31.59.У правильному трикутнику зі стороною 6 на одній зі сторін узято точку на відстані 1 від вершини. Знайти квадрат відстані від цієї точки до центра трикутника.

234

ТЕМА 32. ЧОТИРИКУТНИКИ

Завдання 32.1–32.35 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.

32.1.Сума двох кутів паралелограма дорівнює 130°. Знайти найбільший кут паралелограма.

32.2. Кут між висотами, проведеними з вершини тупого кута паралелограма, дорівнює 48°. Знайти гострий кут паралелограма.

32.3. Периметр паралелограма дорівнює 84 см, а сума двох його сторін — 58 см. Знайти меншу сторону паралелограма.

32.4. Бісектриса гострого кута паралелограма поділяє сторону на відрізки завдовжки 7 см і 10 см, починаючи від вершини тупого кута. Знайти периметр паралелограма.

32.5. У чотирикутнику діагоналі дорівнюють 8 см і 5 см. Обчислити периметр чотирикутника, вершинами якого є середини сторін даного чотирикутника.

32.6. Одна зі сторін прямокутника дорівнює 8 см. Знайти площу прямокутника, якщо площа круга, описаного навколо нього, дорівнює 25π см2.

32.8. У прямокутнику точка перетину діагоналей знаходиться від однієї сторона на 3 см далі, ніж від іншої. Периметр прямокутника дорівнює 28 см. Обчислити меншу сторону прямокутника.

32.9. Діагональ ромба утворює з однією зі сторін кут, що дорівнює 54°. Знайти менший кут ромба.

32.10. Одна з діагоналей ромба дорівнює 30 см. Знайти іншу діагональ ромба, якщо його периметр дорівнює 68 см.

235

32.11. Периметр ромба дорівнює 24 см, а один з його кутів — 120°. Знайти меншу діагональ ромба.

32.12. Обчислити площу ромба, якщо його сторона дорівнює 17 см, а одна з діагоналей — 30 см.

32.13.У ромб, сторона якого дорівнює 20 см, а гострий кут — 30°, вписали коло. Знайти довжину цього кола.

32.14. Сторона ромба дорівнює 6 см, а його площа — 18 см2. Знайти найбільший кут ромба.

32.16.Сторони паралелограма дорівнюють 18 см і 30 см, а висота, яка проведена до більшої сторони, — 6 см. Знайти іншу висоту паралелограма.

32.17.Сторони паралелограма дорівнюють 3 см і 2 см. Обчислити суму квадратів діагоналей паралелограма.

32.18.Діагоналі паралелограма дорівнюють 17 см і 19 см, а одна зі сторін паралелограма — 10 см. Знайти іншу сторону паралелограма.

32.19.Висота рівнобічної трапеції, яка проведена з вершини тупого кута, поділяє основу на відрізки завдовжки 5 см і 11 см. Знайти периметр трапеції, якщо її висота дорівнює 12 см.

32.20.Дві менші сторони прямокутної трапеції дорівнюють а, а один з її кутів — 45°. Визначити площу трапеції.

32.21.Основи трапеції відносяться як 3 : 5, а її висота дорівнює 9 см. Знайти основи трапеції, якщо її площа дорівнює 270 см2.

236

32.22.Висоти паралелограма дорівнюють h1 i h2, а кут між ними — α. Визначити площу паралелограма.

32.23. Діагоналі прямокутника утворюють кут 50°. Знайти кут між діагоналлю прямокутника та бісектрисою кута, проведеними з однієї вершини.

32.25. Менша основа трапеції дорівнює 20 см. Точка перетину діагоналей віддалена від основ на 5 см і 6 см. Знайти площу трапеції.

32.26.Відстань між серединами діагоналей трапеції дорівнює 7 см, а менша її основа — 6 см. Знайти середню лінію трапеції.

32.27. У рівнобічну трапецію вписане коло. Знайти у квадратних сантиметрах площу трапеції, якщо її основи дорівнюють 2 см і 8 см.

32.28. Діагоналі рівнобічної трапеції перпендикулярні. Знайти площу трапеції, якщо її основи дорівнюють 8 см і 20 см.

237

32.30.Бічна сторона рівнобічної трапеції дорівнює 20 см, а її діагональ утворює з більшою основою кут, синус якого дорівнює 0,8. Знайти діаметр кола, описаного навколо цієї трапеції.

32.31. Одна з діагоналей паралелограма дорівнює d і поділяє його гострий кут на кути α і β. Визначити площу паралелограма.

32.32.У ромбі АВСD більша діагональ АС поділяє висоту ВK на відрізки ВМ = 5 см і МK = 3 см. Знайти площу ромба.

32.34. У рівнобічній трапеції діагональ є бісектрисою гострого кута й утворює з більшою основою кут 30°. Знайти периметр трапеції, якщо більша основа дорівнює 8 см.

32.35. Периметр паралелограма більший від однієї з його сторін на 23 см і більший на 19 см від іншої його сторони. Знайти периметр паралелограма.

Завдання 32.36–32.42 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).

32.36. Установитивідповідністьміжфігурами(1–4) таїхнімихарактернимивластивостями(А–Д).

238

32.37.Установити відповідність між початками суджень (1–4) та їх закінченнями (А–Д) так, щоб утворилися істинні судження.

тільки тоді, коли...

32.38. Діагональ ромба утворює зі стороною кут 60°. Установити відповідність між довжинами сторін (1–4) ромба і площами (А–Д) прямокутників з вершинами на серединах сторін ромба.

32.39.Сторони паралелограма дорівнюють 12 см і 5 см. Установити відповідність між величинами гострих кутів (1–4) паралелограмів і їх площами (А–Д).

32.40.У рівнобічних трапеціях діагональ є бісектрисою гострого кута й утворює з більшою основою кут 30°. Установити відповідність між довжинами більших основ (1–4) та периметрами трапецій (А–Д).

32.41. Установити відповідність між задачами (1–4) та відповідями (А–Д) до них.

239

32.42. Установити відповідність між задачами (1–4) та відповідями (А–Д) до них.

4M, N, K і P — середини сторін довільного чотирикутника ABCD, сполучено між собою у вказаній послідовності. Сторона MN утвореного чотирикутника дорівнює 20 см, NK = 8 3 см, KNM = 60°. Знайти площу чотирикутника ABCD

Розв’яжіть завдання 32.43–32.71. Відповідь запишіть десятковим дробом.

32.43.Перпендикуляр, проведений з вершини прямокутника на діагональ, дорівнює 12 і поділяє діагональ на відрізки, різниця яких дорівнює 7. Знайти площу прямокутника.

32.44.Сторони прямокутника відносяться як 3 : 4, а бісектриса прямого кута ділить діагональ на відрізки, різниця яких дорівнює 10 см. Знайти в сантиметрах периметр прямокутника.

32.45.У прямокутнику точка перетину діагоналей міститься на 3 см далі від меншої сторони прямокутника, ніж від його більшої сторони, а периметр прямокутника дорівнює 28 см. Знайти в сантиметрах довжину меншої сторони прямокутника.

32.46.Одна з діагоналей паралелограма дорівнює 6 6 і утворює зі стороною паралелограма кут 60°. Знайти іншу діагональ, якщо вона утворює з тією ж стороною кут 45°.

32.47.Одна зі сторін паралелограма дорівнює 20 см, менша діагональ — 28 см, а гострий кут — 60°. Знайти в сантиметрах периметр паралелограма.

32.48.Одна з діагоналей паралелограма, яка дорівнює 3 6 , утворює з основою паралелограма кут 60°. Обчислити довжину другої діагоналі, якщо вона утворює з цією ж основою кут 45°.

32.49.Висоти паралелограма дорівнюють 4 і 6, а його периметр — 40. Знайти у градусах гострий кут паралелограма.

32.50.Одна сторона паралелограма на 2 більша за іншу, а його діагоналі дорівнюють 8 і 14. Знайти периметр паралелограма.

32.51.Діагоналі ромба відносяться як 3 : 4. Знайти висоту ромба, якщо його периметр дорівнює 80.

32.52.Діагоналі ромба дорівнюють 30 см і 40 см. Обчислити в сантиметрах довжину меншого з відрізків, на які ділить висота, проведена з вершини тупого кута ромба, його сторону.

32.53.Діагоналі ромба дорівнюють 6 см і 8 см. 3 точки перетину діагоналей ромба до його сторін проведено перпендикуляри. Знайти в сантиметрах периметр чотирикутника, вершинами якого є основи цих перпендикулярів.

32.54.Сума довжин діагоналей ромба дорівнює l, а площа ромба — S. Визначити сторону ромба й обчисли її значення, якщо l = 5, S = 4.

32.55.Висота ромба дорівнює 1,2 м, а його сторона — 1,69 м. Знайти у метрах меншу діагональ ромба.

32.56.Визначити площу паралелограма за його висотами h1 і h2 та периметром Р й обчислити її зна-

чення, якщо h1 = 3, h2 = 7, Р = 20.

32.57.Основи трапеції дорівнюють 10 і 24, а бічні сторони — 15 і 13. Знайти площу трапеції.

240