
ТЕСТИ_ЗНО_МАТЕМ
.pdf
ТЕМА 30. ПРЯМОКУТНИЙ ТРИКУТНИК
Завдання 30.1–30.32 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.
30.1.Один з гострих кутів прямокутного трикутника на 18° більший від іншого. Знайти більший з цих кутів.
А |
Б |
В |
Г |
Д |
66° |
68° |
36° |
54° |
48° |
|
|
|
|
|
30.2.Катети прямокутного трикутника дорівнюють a і b (a > b). Визначити довжину медіани, проведеної до меншого катета.
А |
Б |
|
В |
Г |
Д |
a2 − b2 |
a2 + b2 |
1 |
a2 + b2 |
a2 + b2 |
a2 + b2 |
2 |
2 |
2 |
|
4 |
4 |
30.3.Катет прямокутного трикутника дорівнює 12 см, а медіана, що проведена до нього, дорівнює 8 см. Знайти інший катет трикутника.
А |
Б |
В |
Г |
Д |
8 см |
2 7 см |
4 5 см |
12 см |
8 5 см |
|
|
|
|
|
30.4.Один з катетів і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см. Знайти площу трикутника.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
65 см2 |
32,5 см2 |
30 см2 |
60 см2 |
130 см2 |
30.5.Катети прямокутного трикутника дорівнюють 60 см і 80 см. Знайти висоту трикутника, проведену до гіпотенузи.
А |
Б |
В |
Г |
Д |
24 см |
36 см |
48 см |
56 см |
96 см |
30.6.Катет та гіпотенуза прямокутного трикутника відповідно дорівнюють 10 см і 26 см. Знайти проекцію цього катета на гіпотенузу.
А |
Б |
|
В |
Г |
Д |
|
|
8 см |
5,2 см |
7 |
8 |
см |
2,6 см |
311 |
см |
|
|||||||
|
|
13 |
|
13 |
|
||
30.7.У прямокутному трикутнику довжини катетів відносяться як 4 : 3. Обчислити косинус найменшого кута трикутника.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
0,6 |
0,8 |
0,75 |
0,9 |
0,5 |
|
|
|
|
|
30.8.Знайти гіпотенузу прямокутного трикутника, у якого висота, проведена до гіпотенузи, дорівнює 6 3 см, а проекція одного з катетів на гіпотенузу дорівнює 6 см.
|
А |
|
Б |
В |
|
|
Г |
Д |
|
|
12 см |
|
18 см |
24 см |
|
|
28 см |
32 см |
|
|
|
|
|
|
|
|
|
||
30.9. Довжина гіпотенузи прямокутного трикутника дорівнює |
|
2 |
. Обчислити площу круга, описа- |
||||||
5 |
|||||||||
|
|
|
|
|
|
|
|||
|
ного навколо трикутника. |
|
|
|
|
|
|
||
|
А |
|
Б |
В |
|
|
Г |
Д |
|
|
π |
|
4π |
4π |
|
|
5π |
π2 |
|
|
5 |
|
|
5 |
|
|
|
|
|
221
30.10.Один з катетів прямокутного трикутника дорівнює b, а протилежний до нього кут — β. Визначити радіус кола, описаного навколо трикутника.
|
А |
|
Б |
|
В |
|
Г |
|
Д |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |
|
|
b |
|
|
bsinβ |
|
2b |
|
|
2b |
|
|
|
2sinβ |
|
2cosβ |
|
|
|
|
sinβ |
|
cosβ |
|
|||
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30.11.Гострий кут прямокутного трикутника дорівнює α. Визначити катет, прилеглий до цього кута, якщо радіус кола, вписаного в трикутник, дорівнює r.
А |
|
Б |
|
|
В |
|
|
Г |
|
Д |
|
|
α |
|
α |
|
+ ctg |
α |
|
+ tg |
α |
|
α |
r tg |
2 |
r ctg |
2 |
r 1 |
2 |
r 1 |
2 |
2r ctg |
2 |
30.12.Катети прямокутного трикутника дорівнюють 5 см і 12 см. Знайти радіус кола, вписаного в трикутник.
А |
Б |
В |
Г |
Д |
4 см |
2 см |
8 см |
8,5 см |
6 см |
30.13.Радіус кола, вписаного в прямокутний трикутник, дорівнює 1 дм. Знайти площу цього трикутника, якщо гіпотенуза дорівнює 5 дм.
А |
Б |
В |
Г |
Д |
7 дм2 |
8 дм2 |
9 дм2 |
10 дм2 |
6 дм2 |
30.14.У прямокутному трикутнику один з гострих кутів дорівнює α, а висота, що проведена до гіпотенузи, дорівнює h. Визначити площу трикутника.
|
А |
Б |
В |
|
Г |
|
Д |
|
||
|
|
|
|
|
|
|
|
|
||
|
h2 |
|
2h2 sin 2α |
h2 sin 2α |
|
h2 |
|
|
h2 |
|
|
2sin α |
|
2sin 2α |
|
sin 2α |
|
||||
|
|
|
|
|
|
|||||
30.15.Гострі кути прямокутного трикутника відносяться як 1 : 2. Знайти відношення протилежних їм катетів.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
1 : 2 |
1 : 3 |
1 : 2 |
1 : 3 |
1 : 5 |
|
|
|
|
|
30.16.Один з катетів прямокутного трикутника дорівнює 12 см, а гіпотенуза дорівнює 20 см. Знайти менший з відрізків, на які поділяє гіпотенузу бісектриса прямого кута.
А |
|
|
Б |
В |
Г |
Д |
|
|
8 4 |
см |
6 |
5 |
см |
6 см |
5 см |
4 2 |
см |
|
||||||||
7 |
|
12 |
|
|
|
7 |
|
|
30.17.Бісектриси двох кутів прямокутного трикутника утворюють при перетині кут 79°. Знайти менший гострий кут трикутника.
А |
Б |
В |
Г |
Д |
11° |
17° |
22° |
34° |
44° |
|
|
|
|
|
30.18.У прямокутному трикутнику один з гострих кутів дорівнює 27°. Знайти кут між бісектрисою і висотою трикутника, проведеними з вершини прямого кута.
А |
Б |
В |
Г |
Д |
8° |
16° |
32° |
28° |
18° |
30.19.У прямокутному трикутнику один з гострих кутів дорівнює 32°. Знайти кут між висотою і медіаною, проведеними з вершини прямого кута.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
32° |
26° |
36° |
33° |
23° |
|
|
|
|
|
222
30.20.Довжини катетів прямокутного трикутника дорівнюють 5 см і 12 см. Визначити довжину медіани, проведеної до гіпотенузи.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
13 см |
6,5 см |
6 см |
15 см |
8,5 см |
|
|
|
|
|
30.21.Діаметр кола, описаного навколо прямокутного трикутника, дорівнює 20 см, а довжина одного з катетів — 16 см. Знайти інший катет трикутника.
А |
Б |
В |
Г |
Д |
6 см |
16 41 см |
12 см |
18 см |
2 89 см |
|
|
|
|
|
30.22.У прямокутному трикутнику з гострим кутом 45° бісектриса прямого кута дорівнює 7 см. Знайти гіпотенузу трикутника.
|
А |
Б |
В |
|
|
Г |
Д |
|
|
|
|
|
|
|
|
|
7 см |
14 см |
7 2 см |
|
14 2 см |
7 3 см |
|
|
|
|
|
|
|
|
|
30.23. Довжина гіпотенузи прямокутного трикутника дорівнює |
12 |
см. Обчислити довжину кола, |
|||||
|
описаного навколо цього трикутника. |
|
|
π |
|
|
|
|
|
|
|
|
|
||
|
А |
Б |
В |
|
|
Г |
Д |
|
12 см |
9 см |
6π см |
|
|
12π см |
36 см |
|
|
|
|
|
|
|
π |
30.24.Діаметр кола, описаного навколо прямокутного трикутника, дорівнює 17 см, а один із катетів — 8 см. Знайти інший катет.
А |
Б |
В |
Г |
Д |
10 см |
14 см |
12 см |
15 см |
16 см |
|
|
|
|
|
30.25.Медіана, опущена на гіпотенузу прямокутного трикутника, дорівнює 5 см, а один з катетів — 6 см. Обчисліть довжину іншого катета.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
7 см |
8 см |
9 см |
10 см |
11 см |
|
|
|
|
|
30.26.Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює 25 см, один із катетів — 30 см. Знайти довжини відрізків, на які ділить гіпотенузу висота, проведена до неї.
А |
Б |
В |
Г |
Д |
16 см і 34 см |
20 см і 30 см |
24 см і 26 см |
18 см і 32 см |
12 см і 13 см |
|
|
|
|
|
30.27.Бісектриса прямого кута прямокутного трикутника поділяє гіпотенузу на відрізки у відношенні 3 : 4. У якому відношенні ділить гіпотенузу висота?
А |
Б |
В |
Г |
Д |
|
|
|
|
|
3 : 4 |
3 : 2 |
9 : 16 |
2 : 3 |
1 : 2 |
|
|
|
|
|
30.28.Площа прямокутного трикутника дорівнює 30 см2, а довжина одного з катетів — 12 см. Обчислити довжину іншого катета.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
6 см |
5 см |
10 см |
2,5 см |
15 см |
|
|
|
|
|
30.29.Катети прямокутного трикутника дорівнюють 12 см і 16 см. Знайти висоту трикутника, опущену на гіпотенузу.
А |
Б |
В |
Г |
Д |
18 см |
20 см |
19,2 см |
4,8 см |
9,6 см |
223

30.30.Знайти площу прямокутного трикутника, у якого бісектриса прямого кута ділить гіпотенузу на відрізки завдовжки 4 см і 8 см.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
32 см2 |
16 см2 |
57,6 см2 |
28,8 см2 |
14,4 см2 |
30.31. Гіпотенуза прямокутного трикутника дорівнює 10 см. Якою найбільшою може бути площа трикутника?
А |
Б |
В |
Г |
Д |
75 см2 |
100 см2 |
50 см2 |
25 см2 |
12,5 см2 |
30.32.На сторонах прямокутного трикутника АВС ( С = 90°) побудовані квадрати. Площа квадрата, побудованого на гіпотенузі, дорівнює 400 см2, а різниця площ квадратів, побудованих на катетах, дорівнює 112 см2. Знайти площу трикутника.
C |
S1 |
|
|
S2 |
|
A
 B
B
400 см2
А |
Б |
В |
Г |
Д |
|
|
|
|
|
168 см2 |
84 см2 |
96 см2 |
192 см2 |
48 см2 |
Завдання 30.33–30.39 передбачають установлення відповідності. До кожного рядка, позначеного ЦИФРОЮ, доберіть один відповідник, позначений БУКВОЮ, і поставте позначки на перетині відповідних рядків(цифри) і колонок(букви).
30.33.На рисунку зображено прямокутний трикутник ABC ( С = 90°), його висоту CH, медіану CM і позначено величини деяких його елементів. Установити відповідність між елементами трикутника (1–4) та їхніми величинами (А–Д).
|
|
|
|
|
H |
B |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
5 |
|
|
|
|
|
|
|
||
|
|
A |
20° |
|
|
C |
|
|
|
|
|
|
|||
1 |
MCH |
|
А |
|
5 |
|
|
2 |
CMH |
|
|
2sin 20° |
|||
|
Б |
|
|||||
3 |
СM |
|
5sin20° |
||||
|
В |
50° |
|
|
|||
4 |
СH |
|
|
|
|||
|
Г |
5sin70° |
|||||
|
|
|
|||||
|
|
|
Д 40° |
|
|
||
224
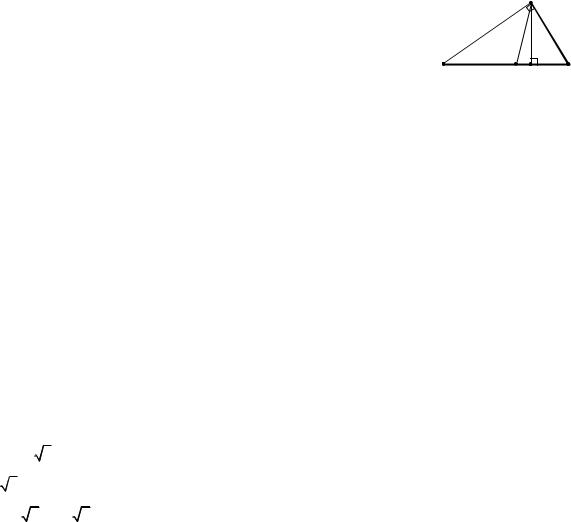
30.34.У прямокутному трикутнику АВС ( С = 90°) проведено бісектрису СK та висоту СH. Установити відповідність між значеннями кута при вершині А (1–4), розміщеній зі сторони бісектриси, і кутом KСH (А–Д).
|
C |
|
A |
K H |
B |
|
|
1 |
8° |
А 27° |
|
2 |
32° |
Б |
33° |
3 |
28° |
В |
37° |
4 |
18° |
Г |
13° |
|
|
Д 17° |
|
30.35.Зовнішній кут при вершині А прямокутного трикутника АВС ( С = 90°) дорівнює 110°. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).
1Знайти кут між більшим катетом і медіаною СМ, проведеною до гіпотенузи
2Обчислити кут між бісектрисою СL та висотою CH
3Знайти кут між медіаною CМ і бісектрисою більшого гострого кута трикутника
4Обчислити кут між медіаною СМ та висотою СН
А 75°
Б 65°
В 20°
Г 25°
Д 50°
30.36.Установити відповідність між катетами а й b (1–4) прямокутних трикутників і значеннями гострого кута, протилежного до катета а (А–Д).
1 |
2 |
см, 2 см |
|
А |
22,5° |
||
2 |
1 |
см, |
3 см |
|
Б |
45° |
|
3 |
|
3 см, 1 см |
|
В |
60° |
||
|
|
Г |
90° |
||||
4 |
2 − |
2 см, |
2 см |
||||
Д 30° |
|||||||
|
|
|
|
|
|||
30.37.Дано прямокутний трикутник, у якому С = 90°, ВС = 3 см, АС = 4 см. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).
1 |
Знайти висоту, проведену до гіпотенузи |
А |
1 см |
2 |
Обчислити проекцію катета АС на гіпотенузу |
Б |
2 см |
3 |
Знайти радіус кола, вписаного в трикутник |
В |
3,2 см |
4 |
Обчислити відстань від вершини В до точки дотику з |
Г |
3 см |
|
гіпотенузою вписаного в трикутник кола |
Д 2,4 см |
|
|
|
||
30.38.Установити відповідність між довжинами гіпотенуз і катетів (1–4) прямокутних трикутників і їх площами (А–Д).
1 |
5 см, 3 см |
А |
84 см2 |
2 |
13 см, 5 см |
Б |
6 см2 |
3 |
10 см, 8 см |
В |
24 см2 |
4 |
25 см, 7 см |
Г |
48 см2 |
|
|
Д 30 см2 |
|
225
15* Капіносов А. Математика. Тести для підготовки до ЗНО
30.39. Установити відповідність між задачами (1–4) та відповідями до них (А–Д).
1 |
Довжина гіпотенузи прямокутного трикутника дорів- |
А |
60 см2 |
|
||||
|
нює |
16 |
см. Знайти площу круга, описаного навколо |
Б |
216 |
см2 |
||
|
π |
В |
150 |
см2 |
||||
|
цього трикутника |
Г |
192 |
см |
2 |
|||
2 |
Медіана та висота прямокутного трикутника, прове- |
|
||||||
Д |
64 см |
2 |
|
|||||
|
дені до гіпотенузи, дорівнюють 12 см і 5 см. Знайти |
|
|
|||||
|
|
|
|
|
|
|||
площу трикутника
3У прямокутному трикутнику бісектриса гострого кута ділить протилежний катет на відрізки 8 см і 10 см. Обчислити площу трикутника
4У прямокутному трикутнику висота, проведена до гіпотенузи, дорівнює 12 см і ділить її на відрізки у відношенні 16 : 9. Обчислити площу трикутника
Розв’яжіть завдання 30.40–30.69. Відповідь запишіть десятковим дробом.
30.40.Бісектриса гострого кута прямокутного трикутника утворює з протилежною стороною кути, один з яких дорівнює 70°. Знайти у градусах менший гострий кут трикутника.
30.41.Катети прямокутного трикутника відносяться як 2 : 1, а гіпотенуза дорівнює 5 5 см. Знайти у сантиметрах більший катет.
30.42.У прямокутному трикутнику катети менші за гіпотенузу на 8 см і 4 см. Знайти в сантиметрах периметр трикутника.
30.43.Катети прямокутного трикутника дорівнюють 15 см і 20 см. Знайти в сантиметрах радіус кола, описаного навколо трикутника.
30.44.Катет прямокутного трикутника дорівнює 12 см, а його гіпотенуза — 20 см. Знайти найменшу медіану трикутника.
30.45.У трикутнику АВС ( С = 90°) СВ = 20 см, tg B = 2,4. Знайти в сантиметрах довжину медіани, проведеної з вершини прямого кута трикутника.
30.46. Відношення катетів прямокутного трикутника дорівнює 0,75, а різниця квадратів катетів — 7 см. Знайти в сантиметрах медіану, проведену до гіпотенузи.
30.47. Катет прямокутного трикутника дорівнює 28 см, різниця двох інших його сторін дорівнює
8см. Знайти у сантиметрах гіпотенузу.
30.48.У прямокутному трикутнику висота і медіана, проведені до гіпотенузи, відповідно дорівнюють
24см і 25 см. Знайти у сантиметрах периметр трикутника.
30.49.У прямокутному трикутнику катет дорівнює 12, а тангенс прилеглого кута дорівнює 5 . Знайти
6
квадрат довжини гіпотенузи.
30.50.Проекції катетів прямокутного трикутника на гіпотенузу дорівнюють 4 см і 21 см. Знайти у сантиметрах менший катет.
30.51.У прямокутному трикутнику АВС до гіпотенузи АВ проведено висоту CD. Площа трикутника BCD дорівнює 16 см2, а площа трикутника ACD — 4 см2. Знайти (у сантиметрах) гіпотенузу трикутника АВС.
30.52. Один з катетів прямокутного трикутника дорівнює 5 см, а проекція іншого катета на гіпотенузу дорівнює 4 см. Знайти у сантиметрах гіпотенузу.
30.53.Висота прямокутного трикутника, опущена на гіпотенузу, ділить її на відрізки 16 см і 9 см. Обчислити в сантиметрах квадратних площу трикутника.
30.54. Точка дотику вписаного в прямокутний трикутник кола ділить гіпотенузу на відрізки 3 см і 10 см. Знайти у квадратних сантиметрах площу трикутника.
226
30.55.Точка дотику вписаного кола ділить гіпотенузу прямокутного трикутника на відрізки, один з яких на 2 см менший від іншого. Знайти площу трикутника (у см2), якщо радіус вписаного кола дорівнює 2 см.
30.56.Гіпотенуза прямокутного трикутника дорівнює 10 см, а синус гострого кута трикутника дорівнює 0,8. Знайти в квадратних сантиметрах площу трикутника.
30.57.Площа прямокутного трикутника дорівнює 150 см2, а котангенс більшого гострого кута трикутника дорівнює 0,75. Знайти в сантиметрах радіус кола, вписаного у трикутник.
30.58.Катети прямокутного трикутника дорівнюють 12 см і 16 см, а гіпотенуза — 20 см. На які відрізки, рахуючи від вершини прямого кута, поділяє сторону трикутника бісектриса меншого гострого кута трикутника. У відповідь записати в сантиметрах потроєну довжину більшого з них.
30.59.Катети прямокутного трикутника дорівнюють 21 см і 28 см. Знайдіть відстань між основами медіани і бісектриси, проведених з вершини прямого кута.
30.60. Точка дотику вписаного в прямокутний трикутник кола ділить гіпотенузу на відрізки 4 см і
6 см. Знайти у сантиметрах радіус вписаного кола.
30.61.Периметр прямокутного трикутника дорівнює 80 см, а його площа дорівнює 240 см2. Знайти (у сантиметрах) діаметр описаного кола.
30.62.Знайти у квадратних сантиметрах площу прямокутного трикутника, якщо його висота ділить гіпотенузу на відрізки 18 см і 32 см.
30.63.Бісектриса прямого кута прямокутного трикутника поділяє гіпотенузу на відрізки, що дорівнюють m і n. Визначити висоту, проведену з вершини прямого кута й обчислити її значення,
якщо m = 3, n = 4.
30.64.У прямокутному трикутнику висота і бісектриса, проведені з вершини прямого кута, відповід-
но дорівнюють h і l. Визначити площу трикутника й обчислити її значення, якщо h = 0,5, l = 0,7.
30.65.У прямокутний трикутник вписано коло радіуса r. Визначити синус меншого гострого кута трикутника, якщо довжина гіпотенузи 5r.
30.66.Висота прямокутного трикутника, проведена з вершини прямого кута, дорівнює h, а відстань
від вершини прямого кута до точки перетину бісектриси меншого гострого кута з меншим катетом дорівнює d. Визначити довжину меншого катета й обчислити її значення, якщо h = 7,
d = 5.
30.67.У прямокутному трикутнику катет дорівнює 12, а гіпотенуза — 13. Знайти квадрат довжини бісектриси трикутника, проведеної з вершини меншого кута.
30.68.Радіус кола, описаного навколо прямокутного трикутника дорівнює 19,5 см, а один із катетів — 36 см. Знайти в сантиметрах інший катет трикутника.
30.69.Від високої тополі падає тінь завдовжки 9 м, а від вертикальної жердини завдовжки 2 м — тінь завдовжки 1,2 м. Знайти висоту тополі.
227
ТЕМА 31. РІВНОБЕДРЕНИЙ ТРИКУТНИК
Завдання 31.1–31.31 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь.
31.1.Знайти периметр рівнобедреного трикутника зі сторонами 3 см і 7 см.
|
А |
Б |
В |
Г |
Д |
|
20 см |
10 см |
13 см |
17 см |
17 см або 13 см |
31.2. У рівнобедреному трикутнику АВС кут С дорівнює 104°. Знайти кут В. |
|
||||
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
|
66° |
76° |
38° |
28° |
48° |
|
|
|
|
|
|
31.3. Кут при основі рівнобедреного трикутника в 4 рази більший за кут при вершині. Знайти кут при вершині трикутника.
А |
Б |
В |
Г |
Д |
20° |
40° |
15° |
120° |
30° |
|
|
|
|
|
31.4.Знайти площу рівнобедреного трикутника, у якого бічна сторона дорівнює 4 2 см, а кут між бічними сторонами дорівнює 30°.
А |
Б |
В |
Г |
Д |
8 2 см2 |
16 3 см2 |
8 3 см2 |
16 см2 |
8 см2 |
|
|
|
|
|
31.5.У рівнобедреному трикутнику бічна сторона дорівнює 10 см, а висота, що проведена до основи, — 6 см. Знайти площу трикутника.
А |
Б |
В |
Г |
Д |
48 см2 |
24 см2 |
96 см2 |
30 см2 |
60 см2 |
31.6.Площа рівнобедреного трикутника дорівнює 12 см2, а довжина його основи — 6 см. Знайти довжину бісектриси, проведеної до основи.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
6 см |
3 см |
8 см |
4 см |
2 см |
|
|
|
|
|
31.7.Бічна сторона та висота рівнобедреного трикутника, проведена до основи, відносяться як 5 : 3. Основа трикутника дорівнює 64 см. Знайдіть периметр трикутника.
А |
Б |
В |
Г |
Д |
112 см |
144 см |
192 см |
48 см |
96 см |
31.8.У рівнобедреному трикутнику висота, проведена до бічної сторони, поділяє її на відрізки 8 см і 2 см, починаючи від вершини кута між бічними сторонами. Знайти площу трикутника.
|
|
|
B |
|
|
|
|
|
|
8 |
|
|
|
|
D |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
A |
|
C |
|
||
А |
Б |
|
В |
|
Г |
Д |
|
|
|
|
|
|
|
78 см2 |
64 см2 |
|
60 см2 |
|
30 см2 |
32 см2 |
228
31.9.У рівнобедреному трикутнику основа дорівнює 6 см, а радіус кола, описаного навколо трикутника, — 5 см. Знайти висоту, проведену до основи.
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
O |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
6 |
C |
|
|
|
|
|
|
D |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
|
А |
Б |
|
|
|
В |
|
|
Г |
Д |
|
|
|
|
|
|
|
|
|
|
|
|
8 см |
9 см |
|
|
|
10 см |
|
|
11 см |
12 см |
31.10. Довжина середньої лінії рівнобедреного трикутника, |
паралельної до основи, дорівнює 2 см. |
|||||||||
|
Обчислити довжину бічної сторони цього трикутника, якщо його периметр дорівнює 16 см. |
|||||||||
|
А |
Б |
|
|
|
В |
|
|
Г |
Д |
|
7 см |
6 см |
|
|
|
5 см |
|
|
4 см |
8 см |
|
|
|
|
|
|
|
||||
31.11. Довжина середньої лінії рівнобедреного трикутника, |
паралельної до його основи, дорівнює |
|||||||||
|
4 см. Обчислити довжину бічної сторони трикутника, якщо його периметр дорівнює 30 см. |
|||||||||
|
А |
Б |
|
|
|
В |
|
|
Г |
Д |
|
|
|
|
|
|
|
|
|
|
|
|
13 см |
22 см |
|
|
|
8 см |
|
|
11 см |
14 см |
31.12.У рівнобедреному трикутнику кут при основі дорівнює α, а радіус кола, вписаного в трикутник, дорівнює r. Визначити бічну сторону трикутника.
B
|
K |
r |
|
|
|
|
O |
|
|
|
A |
D |
C |
|
|
|
|
|
|
А |
Б |
В |
Г |
Д |
rsin α cosα |
r tg α cosα |
r tg α |
r ctg α cosα |
r ctg α |
2 |
2 |
|||
2 |
2 |
cosα |
2 |
cosα |
|
|
|
31.13. Знайти висоту рівностороннього трикутника, сторона якого дорівнює 6 3 см.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
2 см |
3 см |
4 см |
9 см |
12 см |
|
|
|
|
|
31.14. У рівносторонньому трикутнику медіана дорівнює 2 3 см. Обчислити сторону трикутника.
А |
|
Б |
В |
Г |
Д |
||
4 см |
|
4 |
см |
16 см |
3 см |
4 3 см |
|
6 |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
31.15. Знайти площу рівностороннього трикутника зі стороною 2 3 см.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
3 см2 |
3 см2 |
3 3 см2 |
4 3 см2 |
2 3 см2 |
|
|
|
|
|
229
31.16.Обчислити радіус кола описаного навколо рівностороннього трикутника, сторона якого дорівнює 8 3 см.
А |
Б |
|
В |
Г |
Д |
||
6 см |
4 3 см |
|
8 |
см |
8 см |
24 см |
|
3 |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
31.17.Радіус кола, вписаного в рівносторонній трикутник, дорівнює 12 см. Знайти радіус кола, описаного навколо цього трикутника.
А |
Б |
В |
Г |
Д |
36 см |
4 см |
6 см |
24 см |
18 см |
31.18.Радіус кола, вписаного в рівносторонній трикутник, дорівнює 4 3 см. Знайти сторону трикутника.
А |
Б |
В |
Г |
Д |
12 см |
16 см |
24 см |
36 см |
48 см |
31.19. Сторона правильного трикутника дорівнює 20 3 см. Знайти проекцію однієї медіани на іншу.
А |
Б |
В |
Г |
Д |
15 см |
20 см |
30 см |
40 см |
10 3 см |
|
|
|
|
|
31.20. У рівнобедреному трикутнику бісектриси кутів при основі утворюють при перетині кут 52°. Знайти кут між бічними сторонами трикутника.
B
|
K |
O |
L |
|
||
|
|
|
|
|
|
|
|
A |
|
C |
|
||
А |
Б |
|
В |
|
Г |
Д |
72° |
74° |
|
76° |
|
78° |
84° |
|
|
|
|
|
|
|
31.21. О — точка перетину висот АМ і СK рівнобедреного трикутника АВС з основою АС. Знайти кут
В, якщо АОС = 110°.
B
|
K |
O |
M |
|
||
|
|
|
|
|
|
|
|
A |
|
C |
|
||
А |
Б |
|
В |
|
Г |
Д |
70° |
80° |
|
60° |
|
50° |
35° |
31.22. Бічна сторона рівнобедреного трикутника дорівнює 55 см, а висота, що проведена до основи, — 44 см. Знайти відношення відрізків, на які поділяє бічну сторону бісектриса кута при основі.
А |
Б |
В |
Г |
Д |
2 : 3 |
3 : 4 |
4 : 5 |
5 : 6 |
6 : 7 |
31.23.Сторона рівностороннього трикутника дорівнює 8 3 см. Знайти радіус кола, яке проходить через середини сторін трикутника.
А |
Б |
В |
Г |
Д |
2 см |
8 см |
4 см |
4 3 см |
2 3 см |
230
